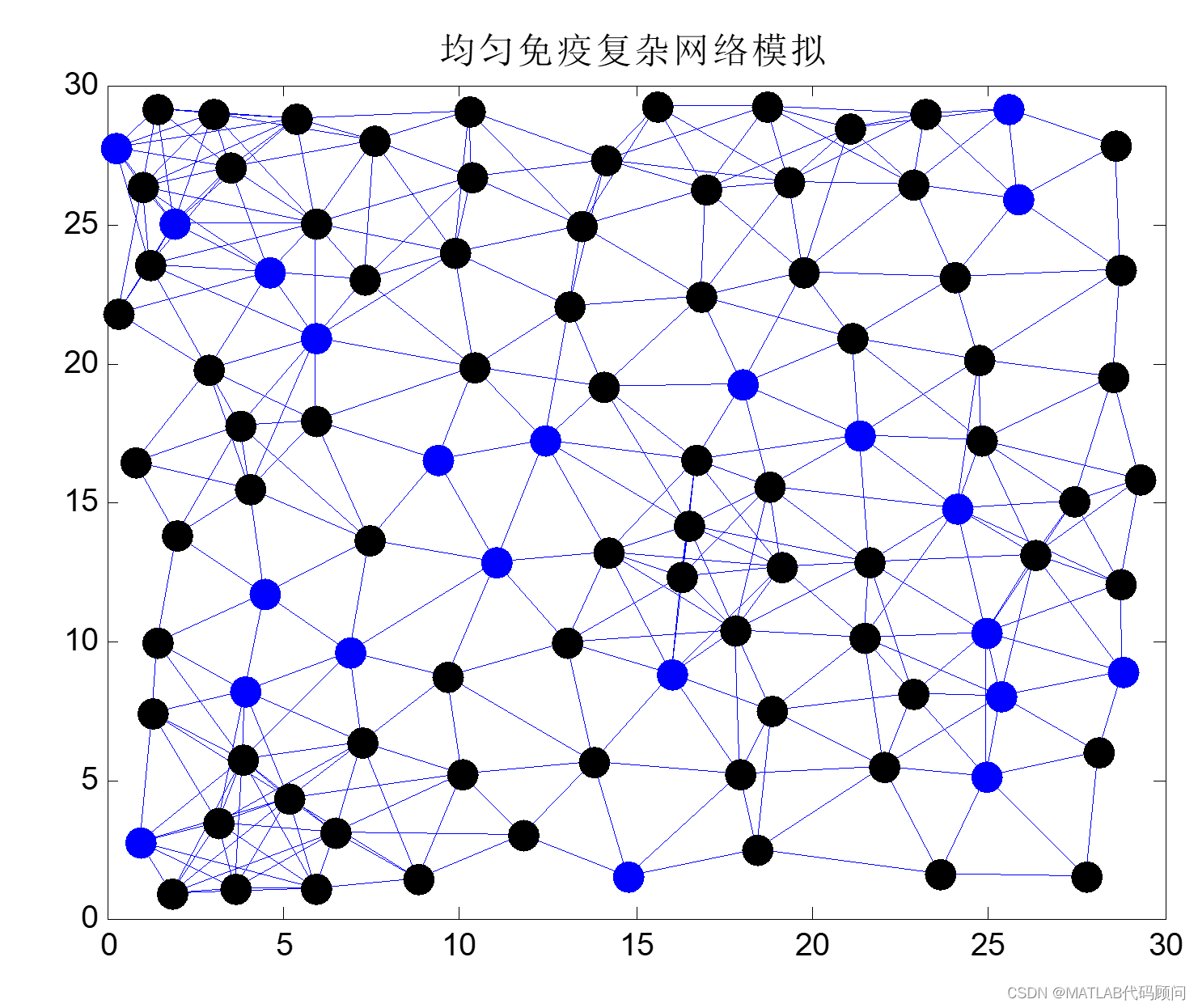
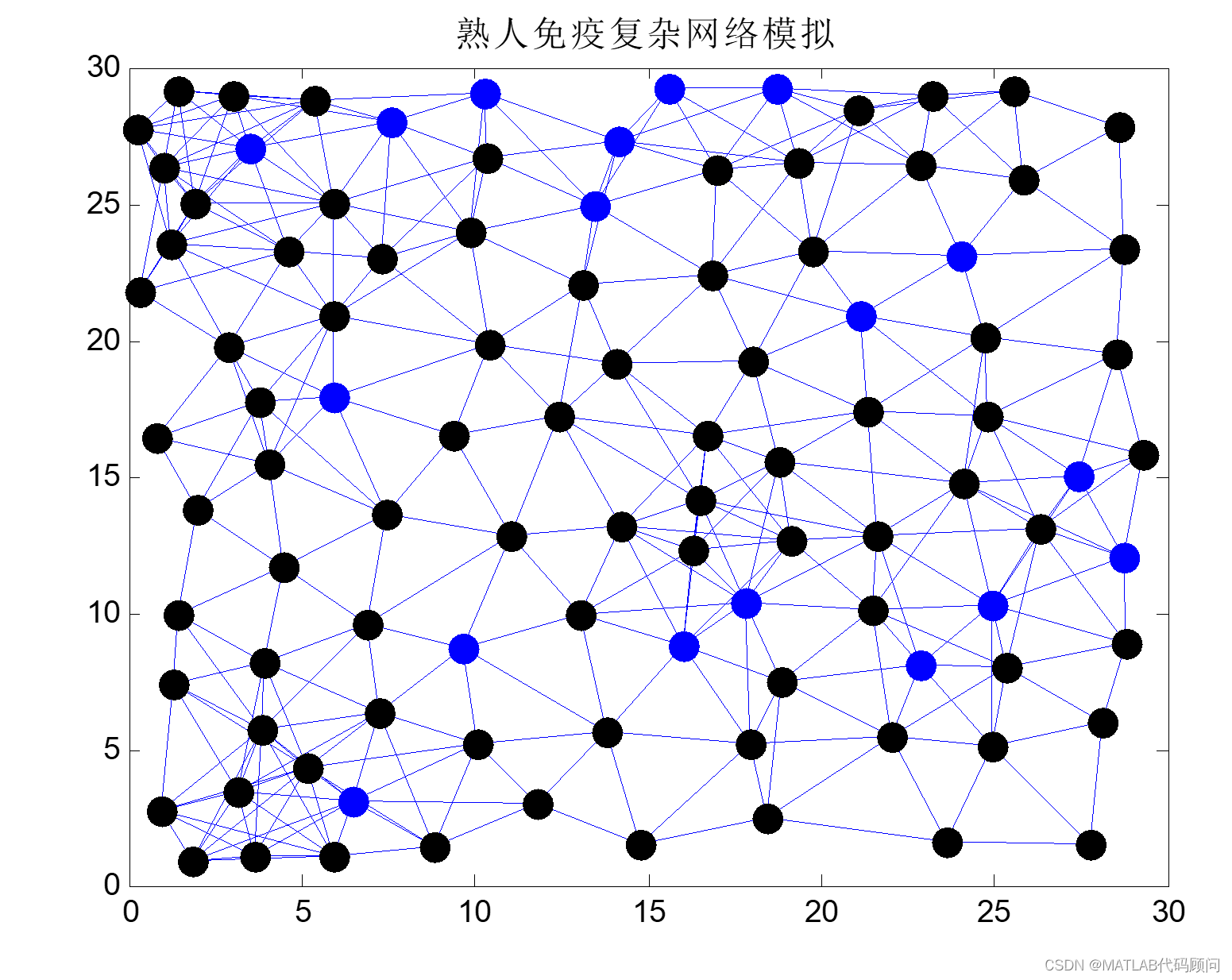
熟人免疫算法是一种用于优化复杂网络的进化算法。它通过模拟熟人关系和免疫机制的思想来改进网络的性能。该算法首先随机生成一组个体作为初始种群,然后通过计算每个个体的适应度值来评估其优劣。接下来,通过选择、交叉和变异等操作,不断迭代更新种群,以期望获得更优的个体。
与传统的遗传算法不同,熟人免疫算法引入了熟人关系的概念。在选择操作中,除了考虑个体自身的适应度值,还考虑了其周围的熟人个体的贡献。这样可以增强种群中优秀个体的传播和保存,从而加速优化过程。
此外,熟人免疫算法还借鉴了免疫机制的思想。通过引入免疫操作,即将一些优秀个体标记为“免疫”个体,可以避免它们被过度交叉和变异而失去优势。这样可以提高算法的收敛性和稳定性。
熟人免疫算法通过结合熟人关系和免疫机制的思想,能够有效地优化复杂网络。它在解决实际问题中具有潜力,并且在网络优化领域有着广泛的应用前景。
主程序如下:
clc;close all;clear all;
disp('随机图生成策略1,2,3或4')
disp('1表示 与均匀随机数比较法,总共生成的边数为N*(N-1)/2*alph');
disp('2表示 概率排序法,总共生成的边数为N*(N-1)/2*alph,并以一定的较小的概率对边随机化重连');
disp('3表示 与均匀随机数比较,但不要求总共的边数为N*(N-1)/2*alph');
disp('4表示 赌轮法,总共生成的边数为N*(N-1)/2*alph');
pp=input('请输入随机图生成策略1,2,3或4:');
% N=input('网络图中节点的总数目N:');
% alph=input('网络图中边的平均连接度alph: ');
% beta=input('表征边的平均长度的参数beta: ');
N=100;
alph=0.25;
beta=0.3;
randData=rand(2,N)*1000;
x=randData(1,:);
y=randData(2,:);
p=lianjiegailv(x,y,alph,beta,N);
switch pp
case 1
A=bian_lianjie1(p,N,alph);
case 2
relink=input('请输入边重新连接的概率:');
A=bian_lianjie2(p,N,alph,relink);
case 3
A=bian_lianjie3(p,N,alph);
case 4
A=bian_lianjie4(p,N,alph);
otherwise
disp('The number pp you input is wrong');
return;
end
plot(x,y,'r.','Markersize',18);
hold on;
for i=1:N
for j=i+1:N
if A(i,j)~=0
plot([x(i),x(j)],[y(i),y(j)],'linewidth',1);
hold on;
end
end
end
hold off
[C,aver_C]=Clustering_Coefficient(A);
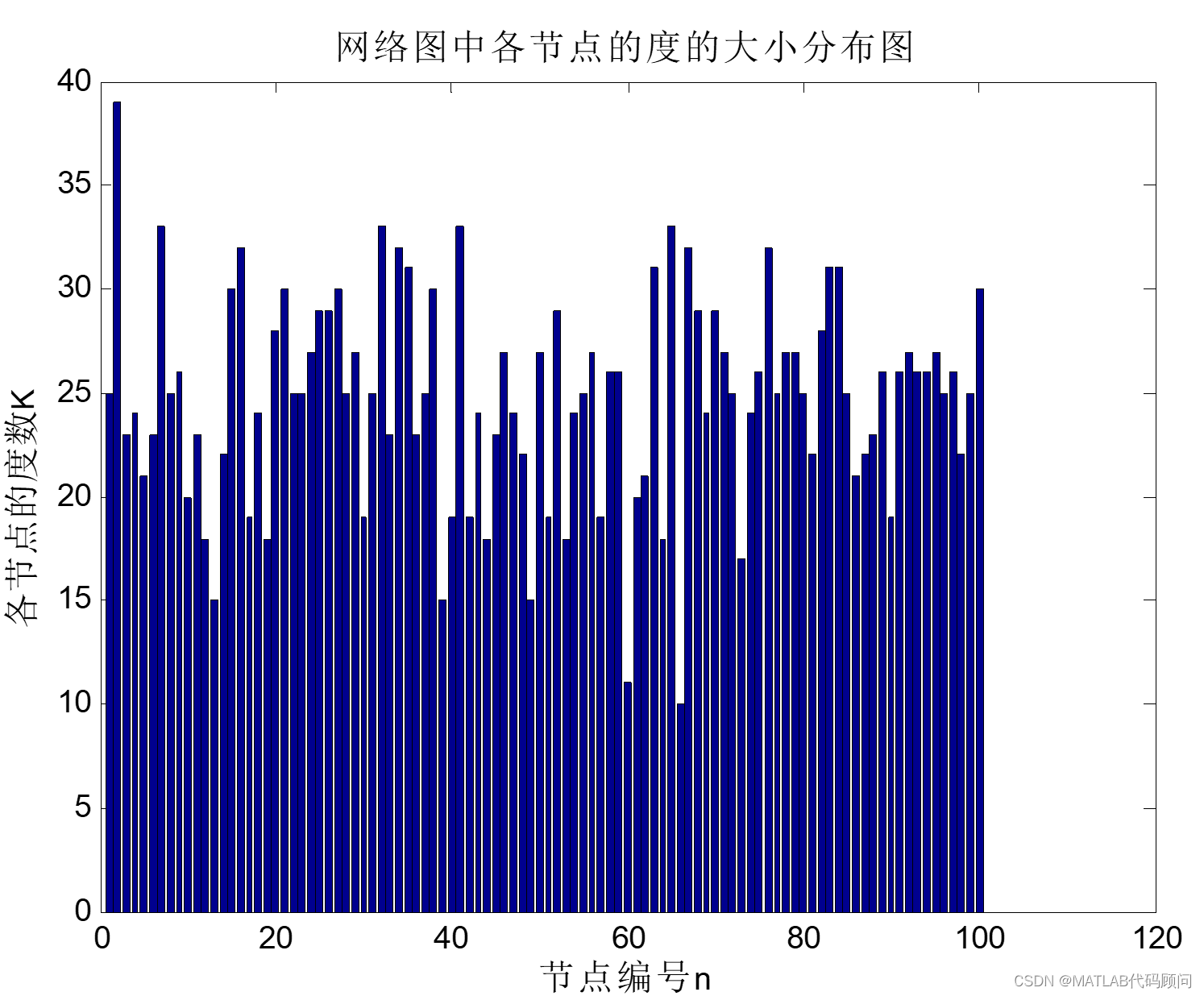
[DeD,aver_DeD]=Degree_Distribution(A);
[D,aver_D]=Aver_Path_Length(A);
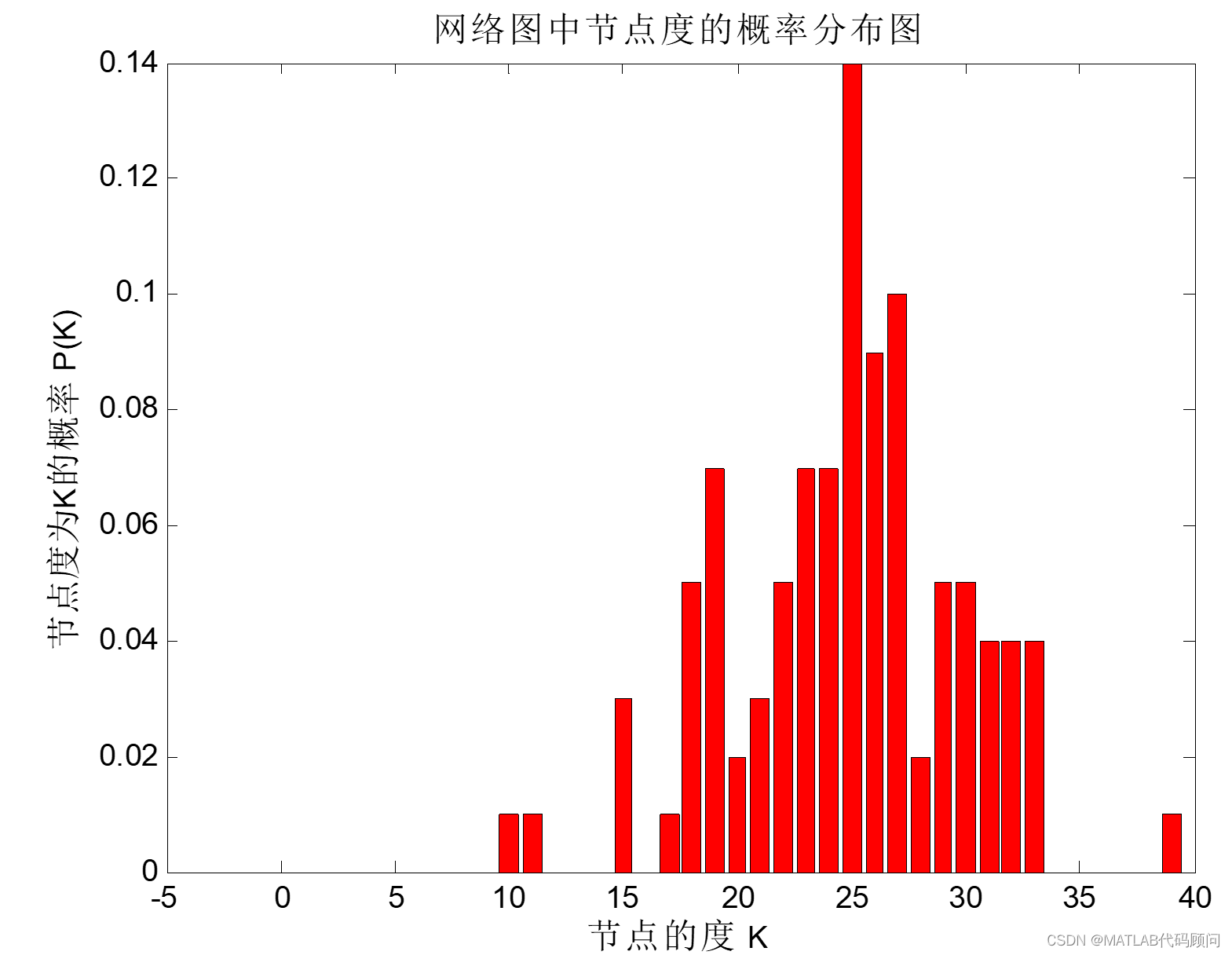
disp(['该随机图的边数为:',int2str(sum(sum(A))/2)]);
disp(['该随机图的平均路径长度为:',num2str(aver_D)]); %%输出该网络的特征参数
disp(['该随机图的聚类系数为:',num2str(aver_C)]);
disp(['该随机图的平均度为:',num2str(aver_DeD)]);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 该函数求解两节点连接边的概率
function p=lianjiegailv(x,y,alph,beta,N)
d=zeros(N);
for i=1:N
for j=1:N
d(i,j)=sqrt((x(i)-x(j))^2+((y(i)-y(j)))^2);
end
end
L=max(max(d));
for i=1:N
for j=1:N
p(i,j)=alph*exp(-d(i,j)/beta/L);
end
p(i,i)=0;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 生成机制1:与[0,1]内均匀随机数比较,若p(i,j)>random_data,则连接节点i,j.
% 直至总共生成的边数为N*(N-1)/2*alph
function A=bian_lianjie1(p,N,alph) % 返回值D为邻接矩阵
A=zeros(N);num=0;
for k=1:inf
for i=1:N
for j=1:N
random_data=rand(1,1);
if p(i,j)>=random_data&A(i,j)==0
A(i,j)=1;A(j,i)=1;
num=num+1;
if num>=N*(N-1)/2*alph
return ;
end
end
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 生成机制2:将概率从大到小排序,连接概率排在前面的节点对,直至总共生成的边数为N*(N-1)/2*alph
%% 以一定的较小的随机随机重连,以实现一定程度的随机化。 有问题!!!!!!!!
function A=bian_lianjie2(p,N,alph,relink)
A=zeros(N);
p1=reshape(tril(p),[1,N*N]);
[p2,px]=sort(p1,'descend');
M=ceil(N*(N-1)/2*alph)
for k=1:M
[m,n]=ind2sub(size(p),px(k)); %单下标索引换为双下标索引
A(m,n)=1;A(n,m)=1;
end
[m,n]=find(tril(A)); %以一定的概率随机化重连
for i=1:length(m)
p1=rand(1,1);
if relink>p1 %若给定的随机化概率大于生成的随机数,则进行重连。
A(m(i),n(i))=0;A(n(i),m(i))=0; %先断开原来的边,再随机选择一条边与之相连
A(m(i),m(i))=inf;
n1=find(A(m(i),:)==0);
random_data=randint(1,1,[1,length(n1)]);
nn=n1(random_data);
A(m(i),nn)=1;A(nn,m(i))=1;
A(m(i),m(i))=0;
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 生成机制3:与[0,1]内均匀随机数比较,若p(i,j)>random_data,则连接节点i,j,
%% 但不要求总共的边数为N*(N-1)/2*alph
function A=bian_lianjie3(p,N,alph);
A=zeros(N);
for i=1:N
for j=1:N
random_data=rand(1,1);
if p(i,j)>=random_data&A(i,j)==0
A(i,j)=1; A(j,i)=1;
end
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%生成机制4:将概率归一化,利用赌轮法选择连接的边,直至生成边数为N*(N-1)/2*alph。
function A=bian_lianjie4(p,N,alph)
A=zeros(N);
p1=reshape(p,1,N*N)./sum(sum(p));
pp=cumsum(p1);%求累计概率
k=0;
while k<N*(N-1)/2*alph %利用赌轮法选择一条边相连
random_data=rand(1,1);
aa=find(pp>=random_data);jj=aa(1); % 节点jj即为用赌轮法选择的节点
j=ceil(jj/N);i=jj-(j-1)*N; %把单下标索引变为双下标索引,或者用函数ind2sub(siz,IND)
% [i,j=ind2sub(size(p),jj);
if A(i,j)==0
A(i,j)=1;A(j,i)=1;
k=k+1;
end
end
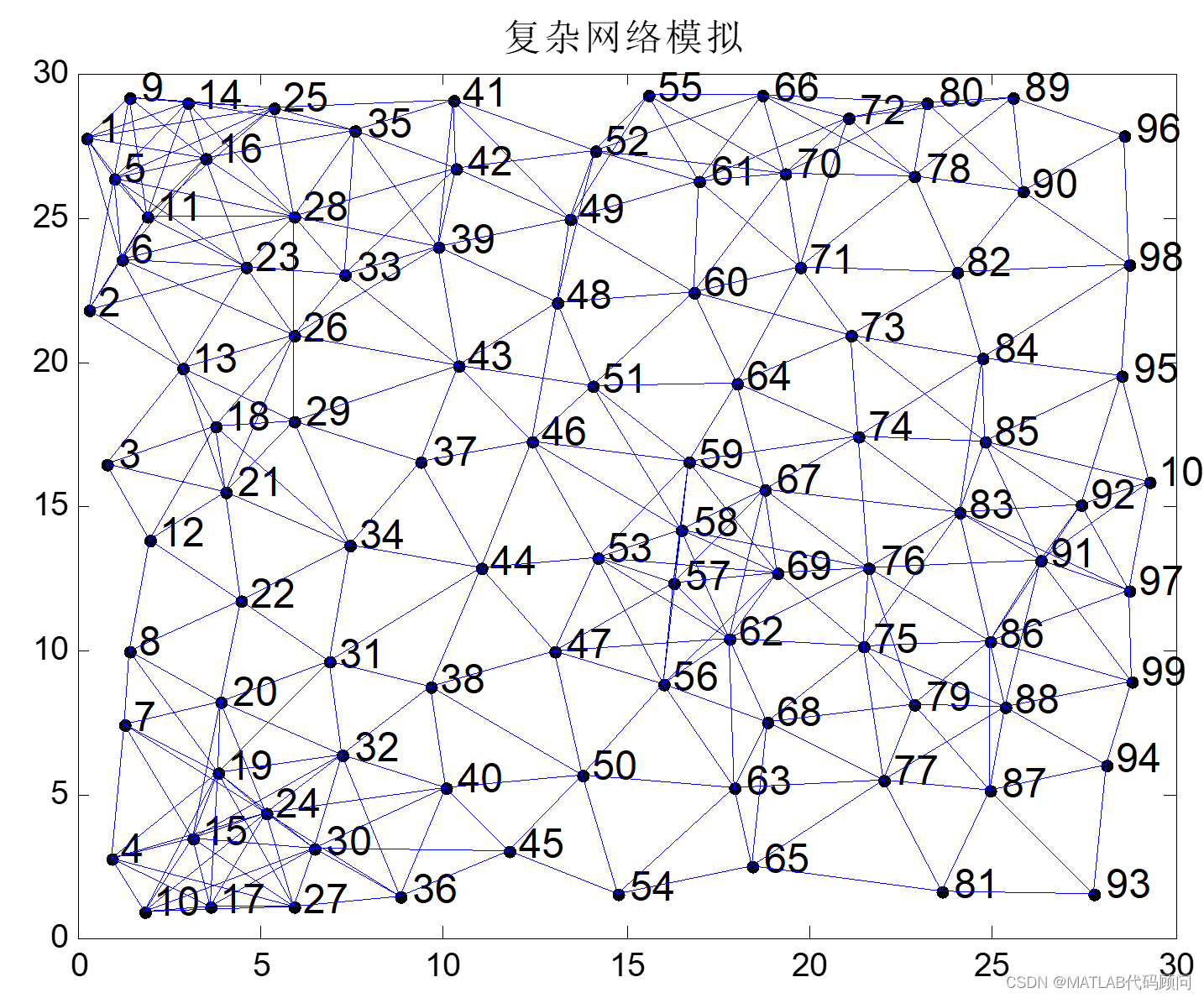
程序结果如下: