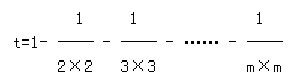有使用过unittest单元测试框架,再使用pytest单元测试框架,就可以明显感觉到pytest比unittest真的简洁、方便很多。
unittest与pytest的区别:
主要从用例编写规则、用例的前置和后置、参数化、断言、用例执行、失败重运行和报告这几个方面比较unittest和pytest的区别



参数化的区别:
unittest参数化:结合装饰器ddt来实现
1 测试类前要添加修饰器 @ddt.ddt@ddt.ddt
2 class TestLogin(unittest.TestCase):#测试用例前要添加修饰 @ddt.data,form_wrong_data包含了3条测试数据,此时要将这3条数据都拿出来,需要加上*
3 @ddt.data(*lg.form_wrong_data)
4 def test_login_2_form_wrongdata(self, data):
5 # 步骤 登录页面 -》 登录功能-》输入用户名、密码 #测试数据 python 断言数据,请输入手机号
6 self.lp.login(data["user"], data["pwd"])
7 self.assertEqual(str(data["check"]), self.lp.get_wrong_msg())pytest参数化:直接使用@pytest.mark.parametrize(自定义命令参数名称,数据源)
@pytest.mark.parametrize("sucess_data", ld.sucess_data)
2 def test_1_sucess_login(self, sucess_data, start_app):
3 MyLog().info("成功登录测试用例")
4 bl(start_app).click_now_to_login()
5 lp(start_app).Login(sucess_data["username"], sucess_data["password"])0最后感谢每一个认真阅读我文章的人,礼尚往来总是要有的,这些资料,对于【软件测试】的朋友来说应该是最全面最完整的备战仓库,虽然不是什么很值钱的东西,如果你用得到的话可以直接拿走:
这些资料,对于【软件测试】的朋友来说应该是最全面最完整的备战仓库,这个仓库也陪伴上万个测试工程师们走过最艰难的路程,希望也能帮助到你!