目录
一.并查集的介绍
二.并查集核心函数介绍
1.查找函数Find()
2.合并函数Union()
一.并查集的介绍
并查集(Disjoint-Set Union,简称并查集)是一种用来管理集合的数据结构。它主要支持两种操作:
1.查找(Find):确定一个元素属于哪个子集。这通常通过找到集合中的代表元素(也称为根节点或代表节点)来实现。
2.合并(Union):将两个子集合并成一个集合。这通常是通过将一个集合的根节点连接到另一个集合的根节点来实现的。
并查集通常用于解决与集合分割和连接相关的问题,例如:
》动态连通性问题:判断图中两个节点是否连通。
》最小生成树算法中的最小边问题:按权重顺序连接图中的边,但要避免形成环。
》社交网络中的好友关系:查找两个用户是否属于同一个社交圈。
通常情况下,并查集通过树结构实现。每个集合都有一个代表元素,而这些集合之间的关系由树的连接来表示。基本的实现方法有两种:
1.基于树的并查集:每个集合用一棵树来表示,其中根节点代表该集合的代表元素。合并操作时,将一棵树的根节点连接到另一棵树的根节点上。这种方法的问题在于树可能会变得不平衡,导致操作的复杂度增加。
2.基于数组的并查集:将集合表示为数组,数组的索引表示元素,数组的值表示元素所属的集合(或者是其父节点)。合并操作时,将其中一个集合的根节点指向另一个集合的根节点。这种方法相对简单,但也容易导致树的深度过大。
并查集的性能取决于其实现方式以及路径压缩和按秩合并等优化技术的使用。
二.并查集核心函数介绍
1.查找函数Find()
查找函数的作用是通过一个节点,往上去查找它的祖先,当某两个节点的祖先相同,那么证明它们两个在同一个集合里面,按照传统的来讲,就是有血缘关系。
下面是循环实现代码:
int Find(int x)
{while(pre[x]!=x)x=pre[x];//继续往上找祖先 return x;//循环出来,当前x为传入元素的祖先
} 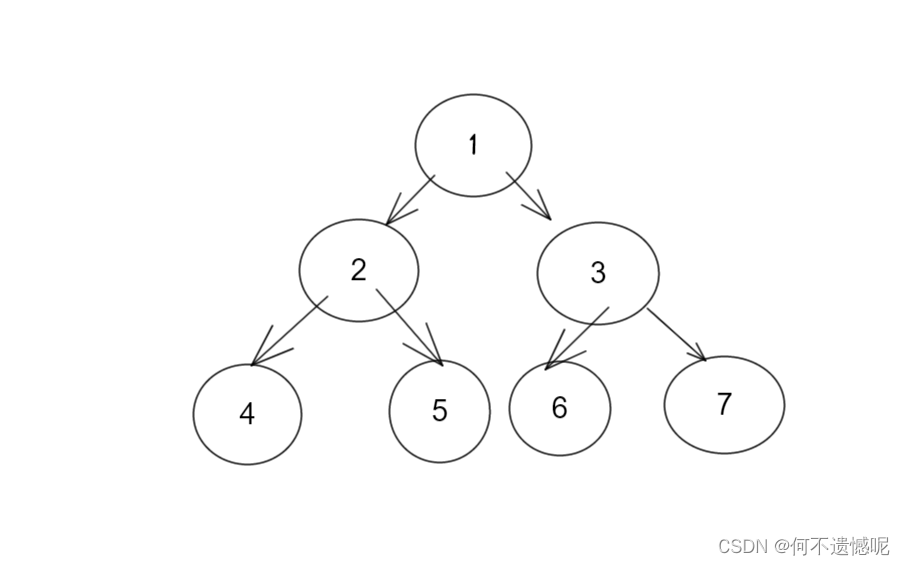
例如,通过这个函数我们传入4进去,可以找到4的祖先2,在找到它们两的祖先1。
但是面对一个庞大的集合,那么查找都要花费很多的时间,那么我们怎么更快的找到祖先呢?
我们设想一下,反正我们的目的是找祖先,那么我们何须注意2和4这类的上下级关系呢,我们直接将2,3,4,5,6,7和祖先1连接在一起不就行了。
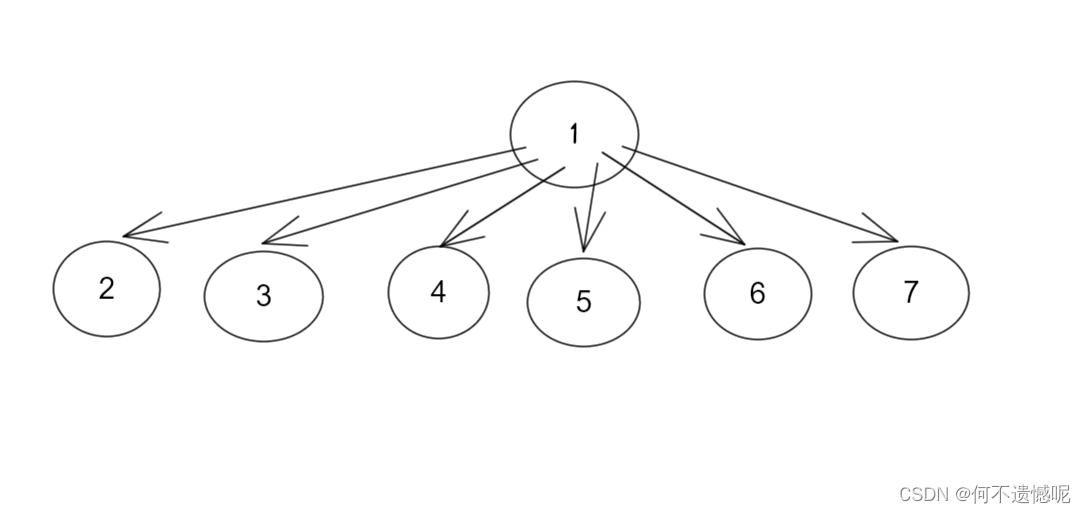
这就用到了我们的路径压缩。
下面是实现代码:
int Find(int x)
{if(pre[x] == x) return x; return pre[x] = Find(pre[x]);
}2.合并函数Union()
合并函数的实现其实非常简单,原理就是找到需要合并的两个节点的的祖先,将某一个的祖先接在另一个祖先上面,他们祖先都接一起了,那么这两个节点当然合并了。
实现代码:
void Union(int x,int y)
{int fx=Find(x),fy=Find(y);if(fx!=fy)//如果祖先不一样则需要合并 pre[fx]=fy;
}那么现在又遇到一个问题,需要合并的两个节点所处的集合高度(规模)不一定相同。
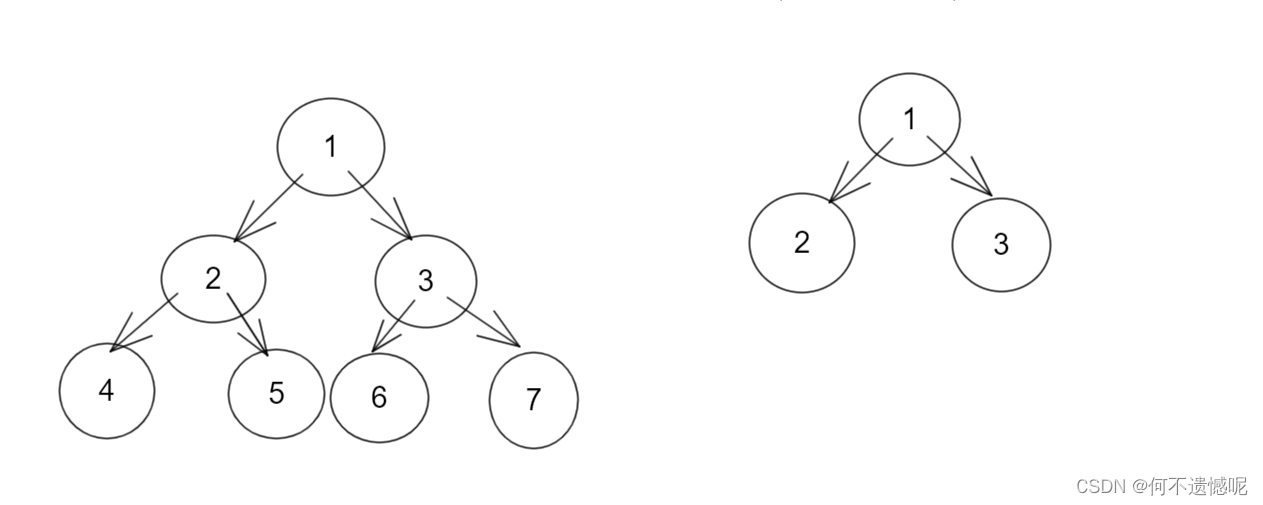
将大树接到小树上,总体树的高度就会变为4,反之,树的高度就会变为3,我们当然是需要我们树的高度越低越好,那么一个怎么实现小树接在大树上呢?
我们可以提前用一个数组表示某个树的高度,合并时按照小树接在大树上面,当接入后,这个树的高度增加。
下面是优化代码:
void Union(int x,int y)
{int fx=Find(x),fy=Find(y);if(fx==fy) return;if(height[fx]>height[fy]) pre[fx]=fy;//按照高度,矮的接到高的上 else if(height[fx]<height[fy]) pre[fy]=fx;else{pre[fy]=fx;//如果一样高 height[fx]++;//将接入的一方+1 }
}