Hello，大家好，我是阿月。坚持刷题，老年痴呆追不上我，今天刷：二叉树的前中后序遍历

题目

分别实现二叉树的前中后序遍历。

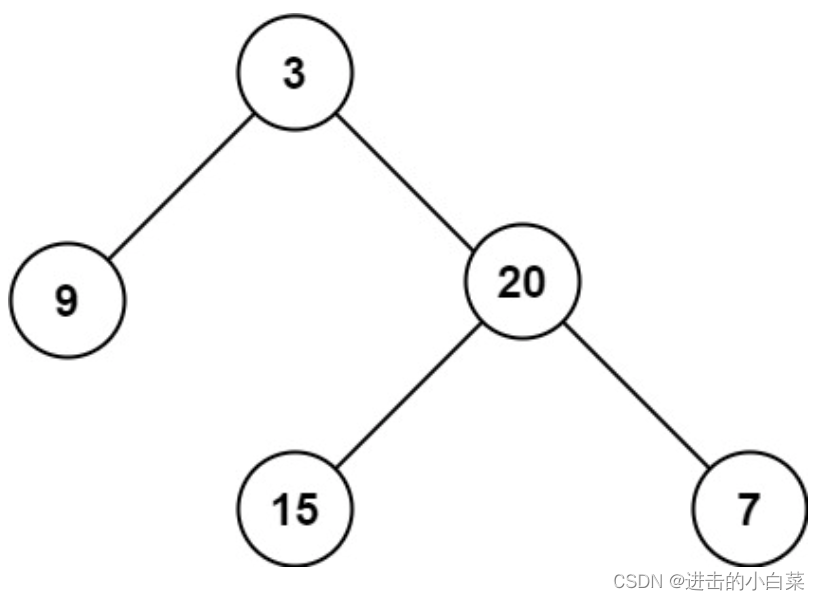
思考

• 前、中、后序遍历分别指的是根节点在查询中的位置
  • 前序遍历：根–>左–>右
  • 中序遍历：左–>根–>右
  • 后续遍历：左–>根–>中
• 二叉树前、中、后序的遍历通常是通过递归或迭代的方式实现对二叉树节点的访问顺序。这些遍历方式是树结构数据存储与检索的基本操作，对于解决与树相关的问题非常重要。

递归实现

递归方式解决二叉树问题最重要的是先知道当前根节点需要做什么，然后再根据函数定义进行递归调用子节点，如何提炼出叶子结点要做的事情也正是二叉树的难点所在。

// 递归法
class Solution {// 前序遍历public  void preorder(TreeNode root, List<Integer> result) {if (root == null) {return;}result.add(root.val);inorder(root.left, result);inorder(root.right, result);}// 中序遍历public  void inorder(TreeNode root, List<Integer> result) {if (root == null) {return;}inorder(root.left, result);result.add(root.val);inorder(root.right, result);}// 后序遍历public  void postorder(TreeNode root, List<Integer> result) {if (root == null) {return;}inorder(root.left, result);inorder(root.right, result);result.add(root.val);}public List<Integer> traversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorder(root, result);return result;}
}

代码使用Java语言通过递归方法实现二叉树的前序、中序和后序遍历：
前序遍历（Preorder Traversal）：

• 访问根节点。
• 递归地对左子树进行前序遍历。
• 递归地对右子树进行前序遍历。

中序遍历（Inorder Traversal）：

• 递归地对左子树进行中序遍历。
• 访问根节点。
• 递归地对右子树进行中序遍历。

后序遍历（Postorder Traversal）：

• 递归地对左子树进行后序遍历。
• 递归地对右子树进行后序遍历。
• 访问根节点。

可以发现在递归实现不同顺序的遍历时，调整的只是对跟节点的访问顺序。

迭代实现

前序遍历

后序遍历的顺序是根节点、左子树、右子树。

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int val) {this.val = val;this.left = null;this.right = null;}
}public class PreorderTraversalIterative {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);  // 将节点值添加到结果列表中// 注意：因为栈是先进后出的结构，所以先将右子节点压栈，再将左子节点压栈if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}return result;}public static void main(String[] args) {// 创建一个二叉树TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);PreorderTraversalIterative traversal = new PreorderTraversalIterative();List<Integer> result = traversal.preorderTraversal(root);System.out.println(result);}
}

• 在迭代的方式来实现前序遍历时，需要通过栈来实现递归的过程。
• 在迭代的过程中，需要合理地利用栈来存储待访问的节点，以及维护遍历顺序的正确性。
• 在前序遍历中，需要先访问根节点，然后是左子树，最后是右子树。因此，在将节点压入栈时，需要保证右子树先于左子树进栈，以确保弹栈顺序的正确性。

后序遍历

后序遍历的顺序是左子树、右子树、根节点。
可通过对前序遍历的代码稍加改动来实现后序遍历：

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int val) {this.val = val;this.left = null;this.right = null;}
}public class PostorderTraversalIterative {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();// 在结果列表的最前面插入节点值，以保证后序遍历的顺序result.add(0, node.val);// 注意：因为栈是先进后出的结构，所以先将左子节点压栈，再将右子节点压栈if (node.left != null) {stack.push(node.left);}if (node.right != null) {stack.push(node.right);}}return result;}public static void main(String[] args) {// 创建一个二叉树TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);PostorderTraversalIterative traversal = new PostorderTraversalIterative();List<Integer> result = traversal.postorderTraversal(root);System.out.println(result);}
}

在后序遍历中，需要在结果列表的最前面插入节点的值，这样可以保证后序遍历的顺序。在迭代过程中，先将左子节点压入栈，再将右子节点压入栈，然后在结果列表的最前面插入根节点的值。

中序遍历

因为中序遍历需要先访问左子树，然后访问根节点，最后访问右子树，所以中序遍历的迭代实现稍微有些不同。过程中需要在沿着左子树一直走到底的时候才能访问根节点，因此在使用迭代实现中序遍历时，需要确保在访问完左子树之后才访问根节点。

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int val) {this.val = val;this.left = null;this.right = null;}
}public class InorderTraversalIterative {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) {return result;}Stack<TreeNode> stack = new Stack<>();TreeNode current = root;while (current != null || !stack.isEmpty()) {// 先将左子树的所有节点压栈while (current != null) {stack.push(current);current = current.left;}// 当前节点为 null 时，表示已经到达左子树的最左边了，可以弹出节点并访问current = stack.pop();result.add(current.val);// 继续遍历右子树current = current.right;}return result;}public static void main(String[] args) {// 创建一个二叉树TreeNode root = new TreeNode(1);root.right = new TreeNode(2);root.right.left = new TreeNode(3);InorderTraversalIterative traversal = new InorderTraversalIterative();List<Integer> result = traversal.inorderTraversal(root);System.out.println(result);}
}

在这个实现中，我们利用了一个栈来模拟递归的过程。我们从根节点开始，一直向左走到最底层的左子树，将沿途遇到的节点压入栈中。然后开始弹出栈顶的节点并访问它，然后转向其右子树，重复这个过程，直到栈为空并且当前节点也为空时，遍历结束。

在前、中、后序的迭代遍历中，为什么都采用栈来模拟递归，而非队列？

• 栈具有先进后出（Last In First Out，LIFO）的特性。
  • 深度优先遍历的特性： 前、中、后序遍历都是深度优先遍历，意味着在遍历时首先访问一个节点，然后深入到其子节点。栈非常适合用于深度优先遍历，因为栈可以保存当前节点，随时回溯到父节点。递归实际上就是在系统调用栈中保存了当前状态，栈结构天然符合深度优先的遍历顺序。
  • 维护遍历顺序： 在前序遍历中，根节点首先被访问，然后是左子树，最后是右子树。在中序遍历中，左子树首先被访问，然后是根节点，最后是右子树。在后序遍历中，左子树和右子树都在根节点之前被访问。这些特性使得使用栈可以方便地维护遍历的顺序。
• 队列具有先进先出（First In First Out，FIFO）的特性。
  • 递归调用的模拟： 在使用栈模拟深度遍历的递归时，每次都将当前节点压入栈中，然后按照特定的顺序访问其子节点，而队列的先进先出（First In First Out，FIFO）特性不太适合模拟此类递归。
  • 如果使用队列来实现迭代的遍历，会导致按照广度优先的顺序遍历树的节点，而前、中、后序的遍历都是深度优先的遍历。

总之，栈在模拟深度优先遍历和维护遍历顺序时更加自然和方便，因此在前、中、后序遍历的迭代实现中常常采用栈来模拟递归。队列则更适合广度优先遍历，比如 坚持刷题 ｜ 二叉树的层序遍历等。