算法42：天际线问题（力扣218题）---线段树-编程知识

218. 天际线问题

城市的 天际线 是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。给你所有建筑物的位置和高度，请返回由这些建筑物形成的 天际线 。

每个建筑物的几何信息由数组 buildings 表示，其中三元组 buildings[i] = [lefti, righti, heighti] 表示：

lefti 是第 i 座建筑物左边缘的 x 坐标。
righti 是第 i 座建筑物右边缘的 x 坐标。
heighti 是第 i 座建筑物的高度。

你可以假设所有的建筑都是完美的长方形，在高度为 0 的绝对平坦的表面上。

天际线 应该表示为由 “关键点” 组成的列表，格式 [[x1,y1],[x2,y2],...] ，并按 x 坐标 进行排序。关键点是水平线段的左端点。列表中最后一个点是最右侧建筑物的终点，y 坐标始终为 0 ，仅用于标记天际线的终点。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

注意：输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[...[2 3], [4 5], [12 7], ...]

示例 1：

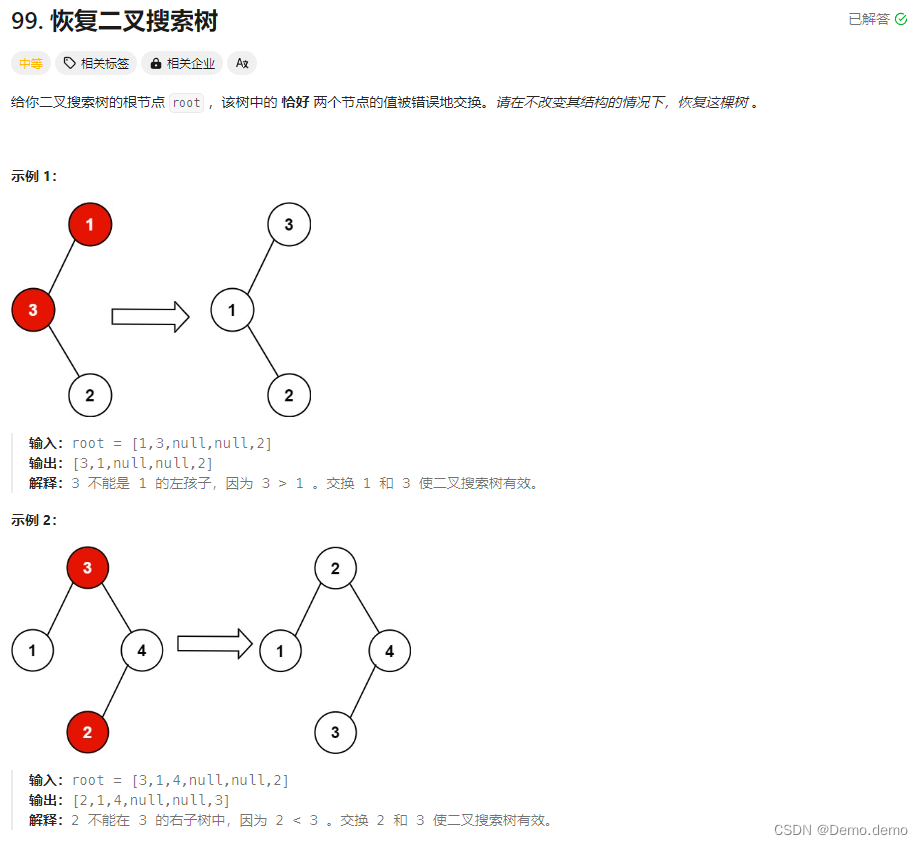
输入：buildings = [[2,9,10],[3,7,15],[5,12,12],[15,20,10],[19,24,8]]
输出：[[2,10],[3,15],[7,12],[12,0],[15,10],[20,8],[24,0]]
解释：
图 A 显示输入的所有建筑物的位置和高度，
图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。

示例 2：

输入：buildings = [[0,2,3],[2,5,3]]
输出：[[0,3],[5,0]]

分析：

这一题看起来很复杂，其实掌握了算法40和算法41的知识点以后，分析起来还是很容易的。

1. 首先，我们观察图片发现，天际线搜集的就是每个建筑物的开始坐标和结束坐标。开始坐标就是建筑物的高度。而结束坐标默认搜集高度为0.

2. 如果有第二个建筑物和第一个建筑物有部分重叠，那么第二个建筑物比第一个建筑物高的话，就搜集第二个建筑物开始位置的横坐标和高度；

如果第二个建筑物比第一个建筑物更宽，说明第二个建筑物把第一个建筑物个住当住了，第二个建筑物比第一个建筑物又高又宽，那么直接放弃第一个建筑物搜集的结束点的横坐标和高度信息；搜集第二个建筑物的坐标和高度替换第一个建筑物的结束点信息。当然，第二个建筑物的结束点高度为0.

3. 建筑物给的顺序，是X轴排好序的。因此，每添加一个建筑物，就搜集一下开始点。结束点是需要判断的；

4. 利用线段树的知识点，首先对X轴坐标进行搜集并确认区间；其次，每一个建筑物都有区间，区间的结束点都默认为0；0代表不更新，如果当前区间被之前的建筑物占领了位置，还保留之前的建筑物坐标信息。

5. 以本题第一个案例来分析，首先搜集X轴坐标并划分区间信息：

有了以上信息，我们接下来就是逐步推导的过程了：

由于天际点搜集的是每个区间的开始位置和结束位置；因此，存在连续、重复的信息应该忽略掉后一个重复值。最终搜集的是：

参照上图，根据区间获取X轴坐标值：

1 区间的 10 1区间对应X轴的2，因此最终是 [2, 10]

2 区间的 15 2区间对应X轴的3，因此最终是 [3, 15]

4 区间的 12 4区间对应X轴的7，因此最终是 [7, 12]

6 区间的 0 6区间对应X轴的12，因此最终是 [12, 0]

7 区间的 10 7区间对应X轴的15，因此最终是 [15, 10]

9 区间的 8 9区间对应X轴的20，因此最终是 [20, 8]

10 区间的 0 10区间对应X轴的24，因此最终是 [24, 0]

最终结果就是 [[2, 10], [3, 15], [7, 12], [12, 0], [15, 10], [20, 8], [24, 0]]

代码实现：

package code04.线段树_02;import java.util.*;//力扣 216，天际线问题 https://leetcode.cn/problems/the-skyline-problem/
public class Code03_SkyLine_2 {class SegmentTree {int[] lines;SegmentTree(int size){lines = new int[size * 4];}//不使用懒更新public void add(int left,int right,int curIndex,int start,int end,int value){//叶子节点if (left == right) {if (left != end) {lines[curIndex] = value > lines[curIndex] ? value : lines[curIndex];}return;}int mid = (left + right)/2;if (start <= mid) {add(left, mid, curIndex * 2, start, end, value);}if (end > mid) {add(mid + 1, right, curIndex * 2 + 1, start, end, value);}}public void query(int left,int right,int curIndex,Map map,List<List<Integer>> list){//叶子节点if (left == right) {/*** 1. 为空直接放入* 2. 不为空，需要判断list最后一个元素*    即最后一个元素的下标为1的位置的值，是否与innerList*    下标为1的值相等。相等则排除，否则加入*/if (list.isEmpty()|| (!list.isEmpty()&& list.get(list.size() - 1) != null&& list.get(list.size() - 1).get(1) != lines[curIndex])) {List<Integer> innerList = new ArrayList<>();//横坐标innerList.add((Integer) map.get(left));//纵坐标innerList.add( lines[curIndex]);list.add(innerList);}return;}int mid = (left + right)/2;query(left, mid, curIndex * 2, map, list);query(mid + 1, right, curIndex * 2 + 1, map, list);}}//根据x轴，按照从左到右、从大到小的顺序编制区间下标public HashMap<Integer, Integer> index(int[][] positions){TreeSet<Integer> pos = new TreeSet<>();//离散化过程,统计开始、结束区间的坐标。//不管数组长度为多少，最终都是落在这些区间中的for (int[] arr : positions) {pos.add(arr[0]);pos.add(arr[1]);}int index = 1;HashMap<Integer, Integer> map = new HashMap<>();//给每个下标编个index，从1开始; 模拟原始线段树的原始数组中给每个元素添加下标的逻辑for (Integer key : pos) {map.put(key, index++);}return map;}//根据区间下标找对应的x轴坐标值public HashMap<Integer, Integer> reverseKeyValue (HashMap<Integer, Integer> map){HashMap reverseMap = new HashMap();for (Iterator iterator = map.keySet().iterator(); iterator.hasNext();) {int key = (int) iterator.next();int value = map.get(key);reverseMap.put(value, key);}return reverseMap;}public List<List<Integer>> getSkyline(int[][] buildings) {//获取到了X轴上对应的下标HashMap<Integer, Integer> map = index(buildings);int size = map.size();SegmentTree tree = new SegmentTree(size);//原始数组的范围int left = 1;int curIndex = 1;int right = size;for (int[] arr : buildings) {//任务的范围int start = map.get(arr[0]);int end = map.get(arr[1]);int value = arr[2];tree.add(left, right, curIndex, start, end, value);}List<List<Integer>> list = new ArrayList<>();HashMap<Integer, Integer> reverseMap = reverseKeyValue(map);tree.query(left, right, curIndex, reverseMap, list);return list;}public static void main(String[] args) {int[][] buildings = {{2,9,10},{3,7,15},{5,12,12},{15,20,10},{19,24,8}};Code03_SkyLine_2 ss = new Code03_SkyLine_2();System.out.println(ss.getSkyline(buildings));}
}

力扣测试结果：

一顿操作猛如虎，结果只打败了 5%，说明代码不够优秀，还需要优化。

优化：

目测我刚刚分析的图片

1、区间的最后一个高度根本就不做考虑，也就是说线段树更新 1 - N，实际上关注的就是 1 到（N-1）的范围；这样的话，add方法内部的

if (left == right) {if (left != end) {lines[curIndex] = value > lines[curIndex] ? value : lines[curIndex];}return;
}

就可以直接去掉 if (left != end) 逻辑判断了。

2. 我们每添加一个建筑物，就递归到子节点。虽然线段树的时间复杂度为O(logN). 但是，执行1次和执行10次这样的时间复杂度方法，时间还是不一样的。因此，需要对目前的add方法进行优化，线段树的懒更新必须加进去

优化代码：

package code04.线段树_02;import java.util.*;//力扣 216，天际线问题 https://leetcode.cn/problems/the-skyline-problem/
public class Code03_SkyLine_2_opt {class SegmentTree {int[] lazy;SegmentTree(int size){lazy = new int[size * 4];}//不使用懒更新public void add(int left,int right,int curIndex,int start,int end,int value){if (start <= left && right <= end) {lazy[curIndex] = value > lazy[curIndex] ? value : lazy[curIndex];return;}int mid = (left + right)/2;pushDown(curIndex);if (start <= mid) {add(left, mid, curIndex * 2, start, end, value);}if (end > mid) {add(mid + 1, right, curIndex * 2 + 1, start, end, value);}}public void pushDown (int curIndex){if (lazy[curIndex] != 0) {lazy[curIndex*2] = lazy[curIndex] > lazy[curIndex * 2] ? lazy[curIndex] : lazy[curIndex * 2] ;lazy[curIndex*2+1] = lazy[curIndex] > lazy[curIndex * 2 + 1] ? lazy[curIndex] : lazy[curIndex * 2 + 1] ;lazy[curIndex] = 0;}}public void query(int left,int right,int curIndex,Map map,List<List<Integer>> list){//叶子节点if (left == right) {if (list.isEmpty()|| (!list.isEmpty()&& list.get(list.size() - 1) != null&& list.get(list.size() - 1).get(1) != lazy[curIndex])) {List<Integer> innerList = new ArrayList<>();//横坐标innerList.add((Integer) map.get(left));//纵坐标innerList.add(lazy[curIndex]);list.add(innerList);}return;}int mid = (left + right)/2;pushDown(curIndex);query(left, mid, curIndex * 2, map, list);query(mid + 1, right, curIndex * 2 + 1, map, list);}}//根据x轴，按照从左到右、从大到小的顺序编制区间下标public HashMap<Integer, Integer> index(int[][] positions){TreeSet<Integer> pos = new TreeSet<>();//离散化过程,统计开始、结束区间的坐标。//不管数组长度为多少，最终都是落在这些区间中的for (int[] arr : positions) {pos.add(arr[0]);pos.add(arr[1]);}int index = 1;HashMap<Integer, Integer> map = new HashMap<>();//给每个下标编个index，从1开始; 模拟原始线段树的原始数组中给每个元素添加下标的逻辑for (Integer key : pos) {map.put(key, index++);}return map;}//根据区间下标找对应的x轴坐标值public HashMap<Integer, Integer> reverseKeyValue (HashMap<Integer, Integer> map){HashMap reverseMap = new HashMap();for (Iterator iterator = map.keySet().iterator(); iterator.hasNext();) {int key = (int) iterator.next();int value = map.get(key);reverseMap.put(value, key);}return reverseMap;}public List<List<Integer>> getSkyline(int[][] buildings) {//获取到了X轴上对应的下标HashMap<Integer, Integer> map = index(buildings);int size = map.size();SegmentTree tree = new SegmentTree(size);//原始数组的范围int left = 1;int curIndex = 1;int right = size;for (int[] arr : buildings) {//任务的范围int start = map.get(arr[0]);int end = map.get(arr[1]);int value = arr[2];//天际线的区间最后一个x坐标的高度信息根本不做考虑，默认就是0.// 因此，start - end的区间，实际考虑的知识 start - (end-1)的范围tree.add(left, right, curIndex, start, end - 1, value);}List<List<Integer>> list = new ArrayList<>();HashMap<Integer, Integer> reverseMap = reverseKeyValue(map);tree.query(left, right, curIndex, reverseMap, list);return list;}public static void main(String[] args) {//int[][] buildings = {{2,9,10},{3,7,15},{5,12,12},{15,20,10},{19,24,8}};//int[][] buildings = {{0,2,3},{2,5,3}};int[][] buildings = {{2,13,10},{10,17,25},{12,20,14}};Code03_SkyLine_2_opt ss = new Code03_SkyLine_2_opt();System.out.println(ss.getSkyline(buildings));}
}

测试结果：打败76%