参考资料:用python动手学统计学
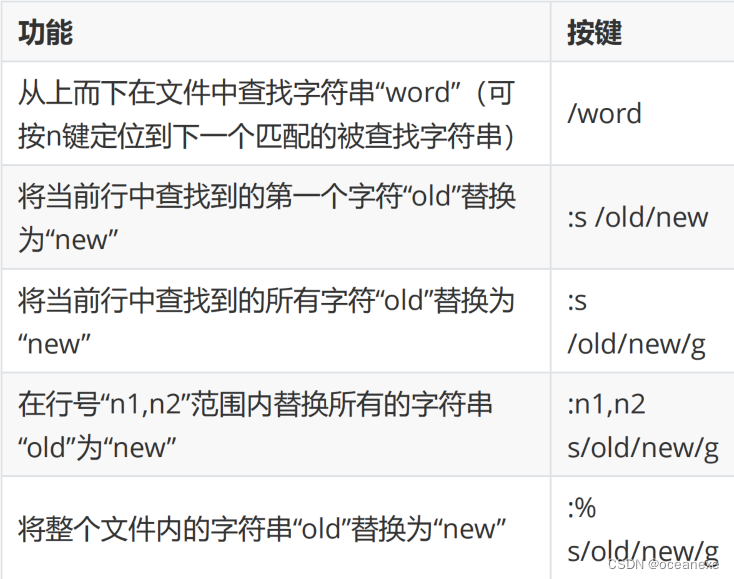
1、t统计量
t统计量的计算公式为:
其中,为样本均值,μ为总体均值,
为实际样本的无偏标准差,N为样本容量。
t统计量的公式与标准化公式类似。t统计量可以理解为对样本均值进行标准化。
2、模拟t分布
2.1 获取t值
# 导入库
import pandas as pd
import numpy as np
import scipy as sp
from scipy import statsimport matplotlib.pyplot as plt
import seaborn as sns# 建立均值为4,标准差为0.8的正态总体
pop=stats.norm(loc=4,scale=0.8)# 设置随机种子,用于复现结果
np.random.seed(1)
# 添加数组用于存放t值
t_value_array=np.zeros(10000)
# 模拟抽样获取t值,并存放至数组
for i in range(0,10000):sample=pop.rvs(size=10)sample_mean=np.mean(sample)sample_std=np.std(sample,ddof=1)sample_se=sample_std/np.sqrt(len(sample))t_value_array[i]=(sample_mean-4)/sample_se2.1 绘制t值分布的直方图
sns.set()
# t值分布直方图,并添加核密度曲线
sns.histplot(t_value_array,kde=True,stat='density')
# 绘制标准正态分布的概率密度曲线
x=np.arange(-8,8.1,0.1)
y=stats.norm.pdf(x=x) # 默认为均值为0,标准差为1的正态分布
plt.plot(x,y,linestyle=":")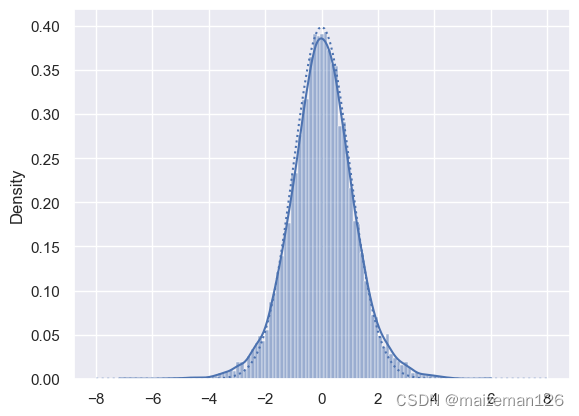
由上图可以看到实线的t分布核密度曲线和虚线的标准正态分布曲线二者没有完全重合。
3、t分布的自由度
若样本容量为N,则N-1为t分布的自由度。当样本容量越大,t分布就约接近于标准正态分布。
4、t分布概率密度曲线和标准正态分布概率密度曲线对比图
x=np.arange(-8,8.1,0.1)
y_u=stats.norm.pdf(x) # 标准正态分布概率密度
y_t=stats.t.pdf(x,df=9) # 自由度为9的t分布概率密度
plt.plot(x,y_t,linestyle="-")
plt.plot(x,y_u,linestyle=":")
t分布相对于标准正态分布更扁平,这是因为t分布以均值的标准误为除数。另外,t分布的数据范围较标正态分布的范围稍大一些,也就是更容易出现远离均值的数据。
5、t分布的意义
t分布的意义就是在总体方差未知时也可以研究样本均值的分布。

![[SWPUCTF 2021 新生赛]include](https://img-blog.csdnimg.cn/direct/5e36a8c8426a408d97af45254267aca2.png)