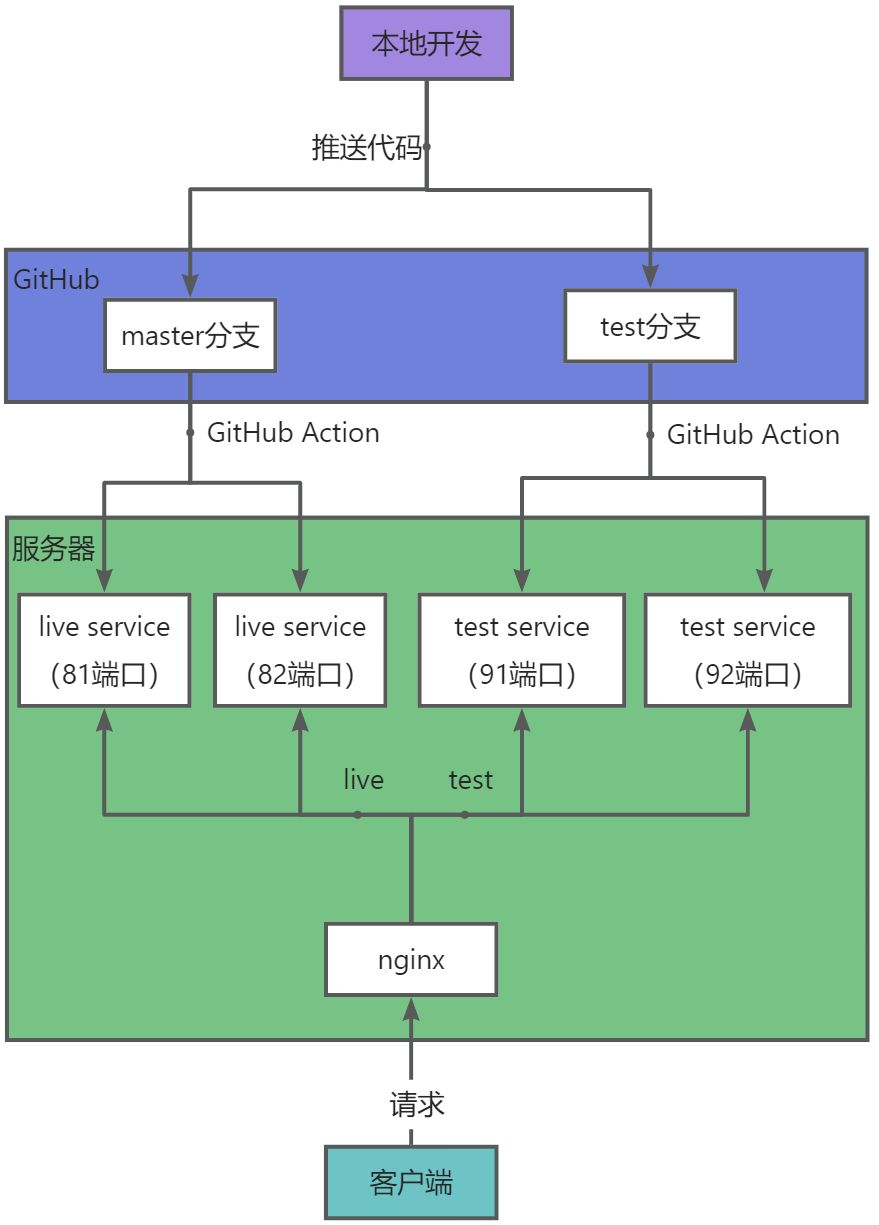
目录
题目描述:
输入描述:
输出描述:
示例1
解法一(C):
解法二(Cpp):

正文开始:
题目描述:
据说著名犹太历史学家 Josephus 有过以下故事:在罗马人占领乔塔帕特后,39 个犹太人与 Josephus 及他的朋友躲到一个洞中,39 个犹太人决定宁愿死也不要被敌人抓到,于是决定了一种自杀方式:41 个人排成一个圆圈,由第 1 个人开始报数,报数到 3 的人就自杀,然后再由下一个人重新报 1,报数到 3 的人再自杀,这样依次下去,直到剩下最后一个人时,那个人可以自由选择自己的命运。这就是著名的约瑟夫问题。现在请用单向环形链表得出最终存活的人的编号。
输入描述:
一行两个整数 n 和 m, n 表示环形链表的长度, m 表示每次报数到 m 就自杀。
输出描述:
输出最后存活下来的人编号(编号从1开始到n)
示例1
输入: 5 2
输出: 3
(备注: 1≤n,m≤1000)
解法一(C):
创建环形链表,通过两个函数实现:
typedef struct ListNode LS;//根据传入的x的值,创建val = x 的新节点
LS* BuyNewnode(int x)
{LS* newnode = (LS*)malloc(sizeof(LS));if(newnode == NULL){perror("malloc");exit(1);}newnode->val = x;newnode->next = NULL;return newnode;
}//将新节点链接起来
LS* CreateL(int n)
{//第一个节点的val的初始值赋值为1LS* phead = BuyNewnode(1);LS* ptail = phead;for(int i = 2;i <= n;i++){ptail->next = BuyNewnode(i);ptail = ptail->next;}ptail->next = phead;//由于链表中删除某一节点,必须能找到前驱节点,如此才能改变前驱节点的next指针的方向//为了在初始时找到头节点的前驱节点,所以CreateL函数选择返回ptailreturn ptail;
}重点:
1. while()的终止条件,当pcur->next == pcur 时,循环终止;(这个时候只剩一个人了)
2. f:计数作用;(表示每个人报的数);pcur 每动一次,f 都跟着变化;并且初始 f 是1;(第一个人也是要报数的)
3. 如果f==m,(这个人要自杀);前驱节点next指针指向pcur的下一个节点;同时把pcur这个节点free掉,pcur后移。
4. 如果f != m,正常报数;pcur向后,prev向后,f++;
主体部分:
int ysf(int n, int m ) {// write code hereLS* ptail = CreateL(n);LS* pcur = ptail->next;LS* prev = ptail;int f = 1;while(pcur->next != pcur){if(f == m){prev->next = pcur->next;free(pcur);pcur = prev->next;f = 1;}else{pcur = pcur->next;prev = prev->next;f++;}}return pcur->val;
}
解法二(Cpp):
(源自 牛客Huster水仙)
将编号改为从0开始,记f(n,m)为原问题的解
由于第一次遍历了0~(m-1)%n,则第二次遍历相当于将整个队伍循环左移了k位(k=m%n)
所以子问题f(n-1,m)的解循环右移k位即为原问题的解f(n,m)
#include<iostream>
#include<queue>
using namespace std;int getans(int n,int m){if(n==1)return 0;else{return (getans(n-1,m)+m)%n;}}int main(){int m,n;while(scanf("%d%d",&n,&m)!=EOF){printf("%d\n",getans(n,m)+1);}return 0;
}
完~
未经作者同意禁止转载