文章目录
- 并查集
- 1.朴素版本
- 2.路径压缩
- 3.按秩合并
- 4.启发式合并
- 5.练习题
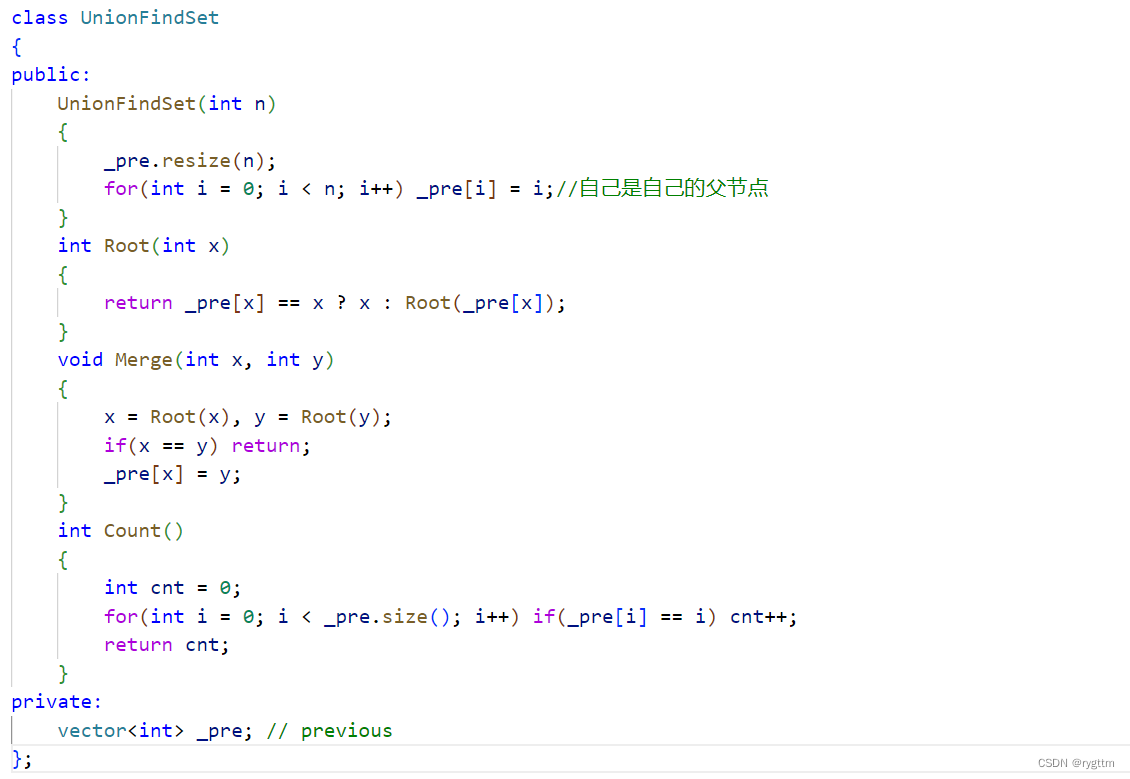
并查集
1.朴素版本
1.
并查集解决的是连通块的问题,常见操作有,判断两个元素是否在同一个连通块当中,两个非同一连通块的元素合并到一个连通块当中。
并查集和堆的结构类似,都是采用数组存储下一个节点的下标的方式来抽象成一棵树,只不过堆的数组对应的是一棵二叉树,而并查集的数组对应的是森林,可以抽象成很多的树,并且每棵树也不一定是二叉树,任意形状均可。
初始化数组时,数组存储内容均为自己的下标,表示每个节点的父节点都是自己,previous译为先前的,在这里正好表示某一个元素的父节点元素下标是多少。
合并两个节点,实际上是合并这两个节点分别对应的根节点,这里可能会有人有疑问,为什么不合并非根节点呢?如果你合并非根节点,让非根节点指向另一个非根节点,那么2棵树直接变成三棵树了。并查集合并算法的性能瓶颈其实是在找根的操作上,如果一棵树的高度是N,那么找根的时间复杂度其实就是O(N)了,这样的效率实际上是很低的,所以后面会进行三种方式的优化。
统计并查集中树的个数其实也比较简单,只需要统计根节点是自己的节点个数即可。
2.路径压缩
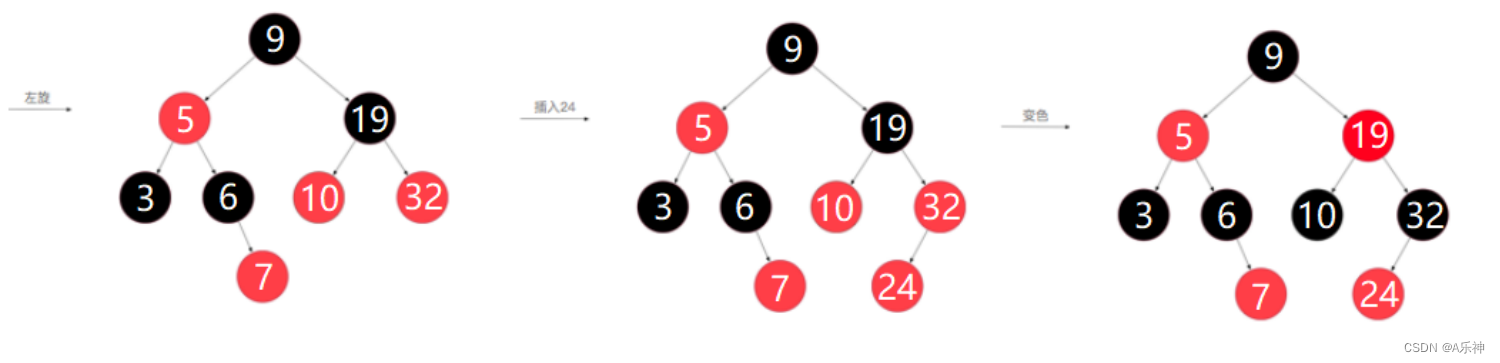
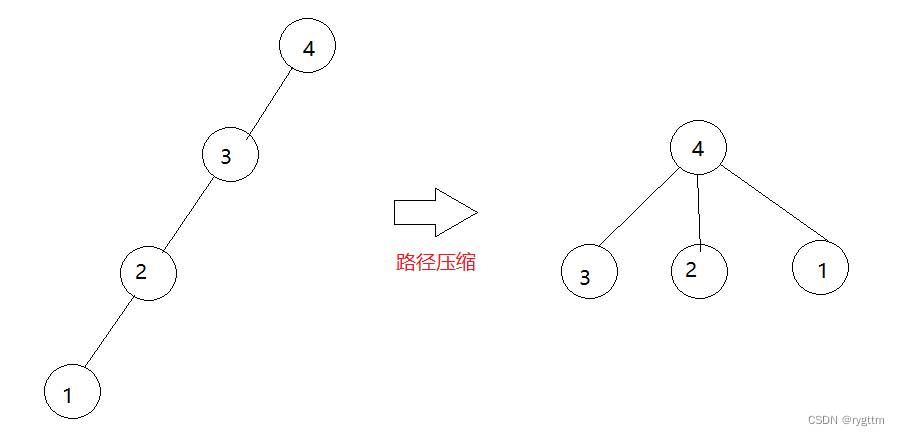
如果我们能够缩短查找根节点过程中的路径,那么合并两棵树的效率就会很高,如下图所示,如果路径压缩到一层,那么查找根的时间复杂度就接近于O(1),所以路径压缩这种方式效率是很高的。
下面的图其实主要想给大家展示路径压缩的好处,但在我们的代码里面,左边这种单分支情况的树一定是不会出现的,因为每次任意两棵树合并时,在查找根期间都会做路径压缩,从节点个数为1开始进行任意树的合并,一定是不会出现左边这种4个节点串起来的情况的,所以下面的图仅仅是为了展示路径压缩的优点而已。
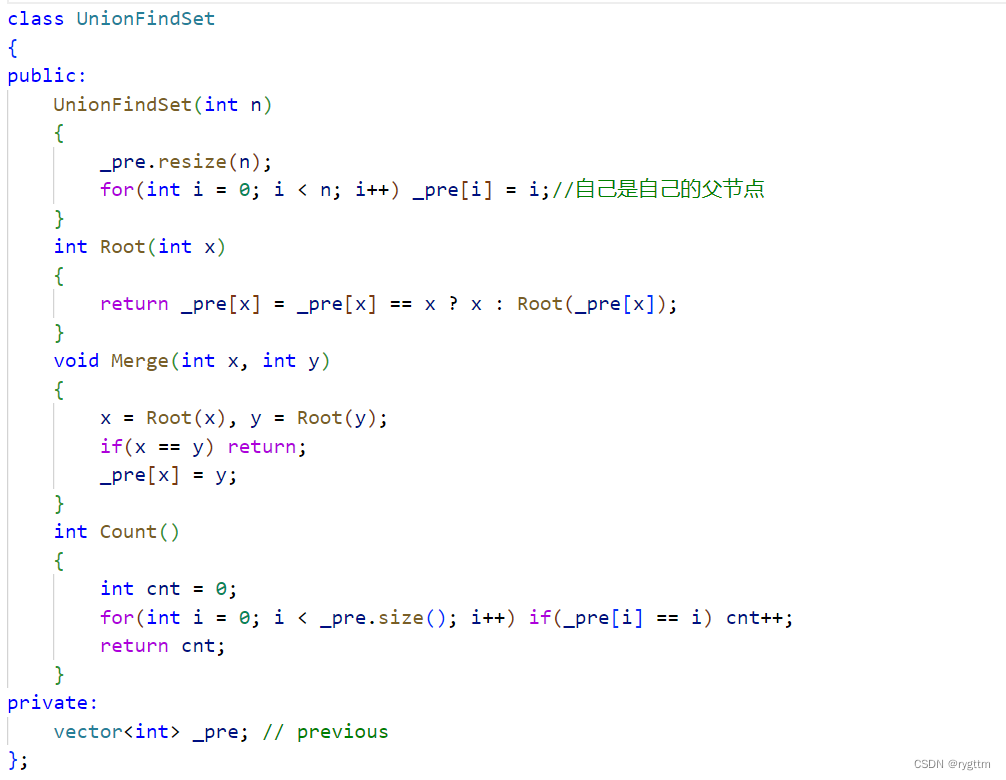
下面是递归版本的压缩路径
下面是循环版本的压缩路径
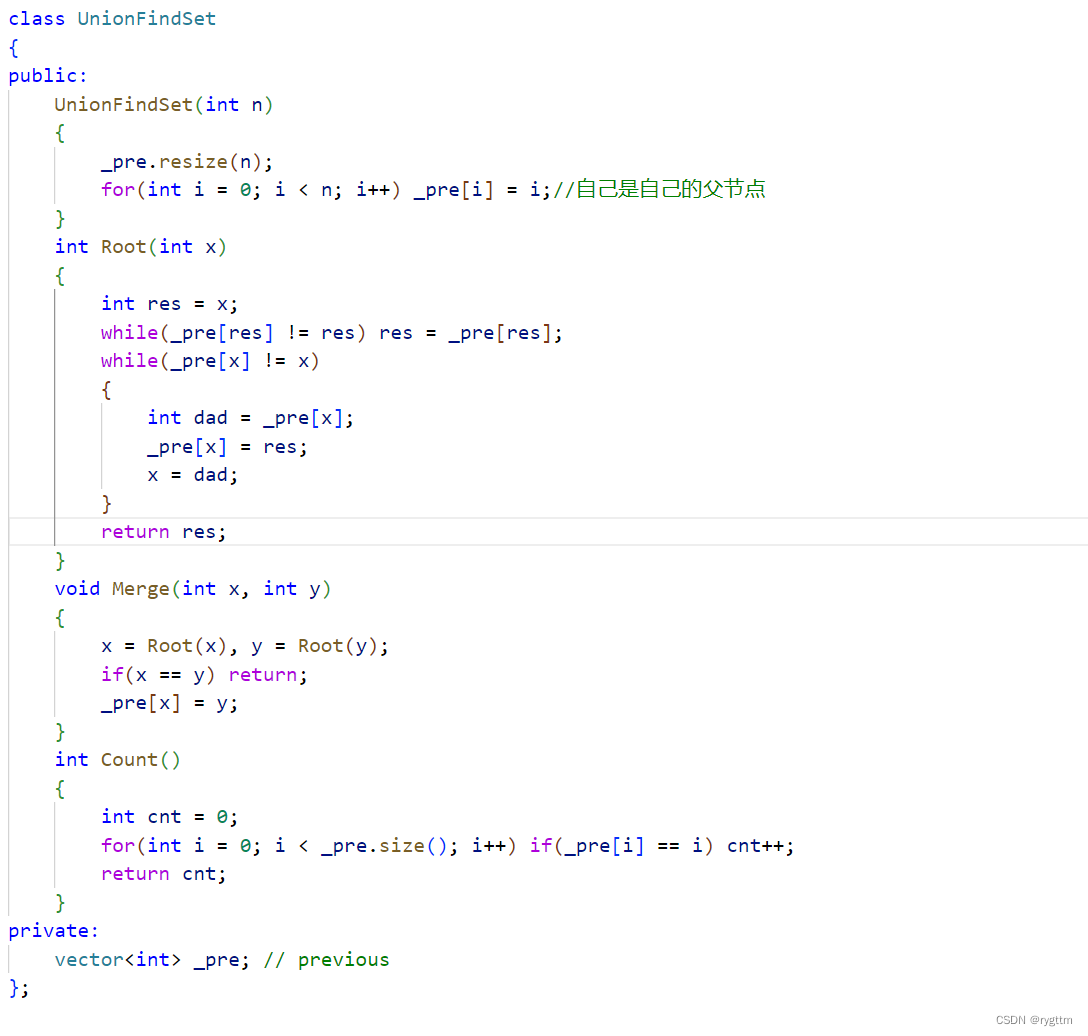
3.按秩合并
秩的英文是rank,rank还有排名等意思,但在并查集这里秩其实表示的是树的高度,当两棵树合并时,为了让合并后的效率更高,我们通常选择将树高度小于等于另一棵树的树主动合并到较高的那棵树上去,这样有一个好处,树整体的高度可能不会改变或者是增加1,这两种情况都是比较好的。
那么如何维护树的高度呢?我们只需要一个rnk数组即可,在合并的时候判断两棵树的高低,将较小的树合并到较大树上,同时维护rnk数组,如果两棵树高度相等,合并操作无所谓,例如x合并到y上,那么y的高度需要+1,x的高度不变。时间复杂度近似于O(logN)。
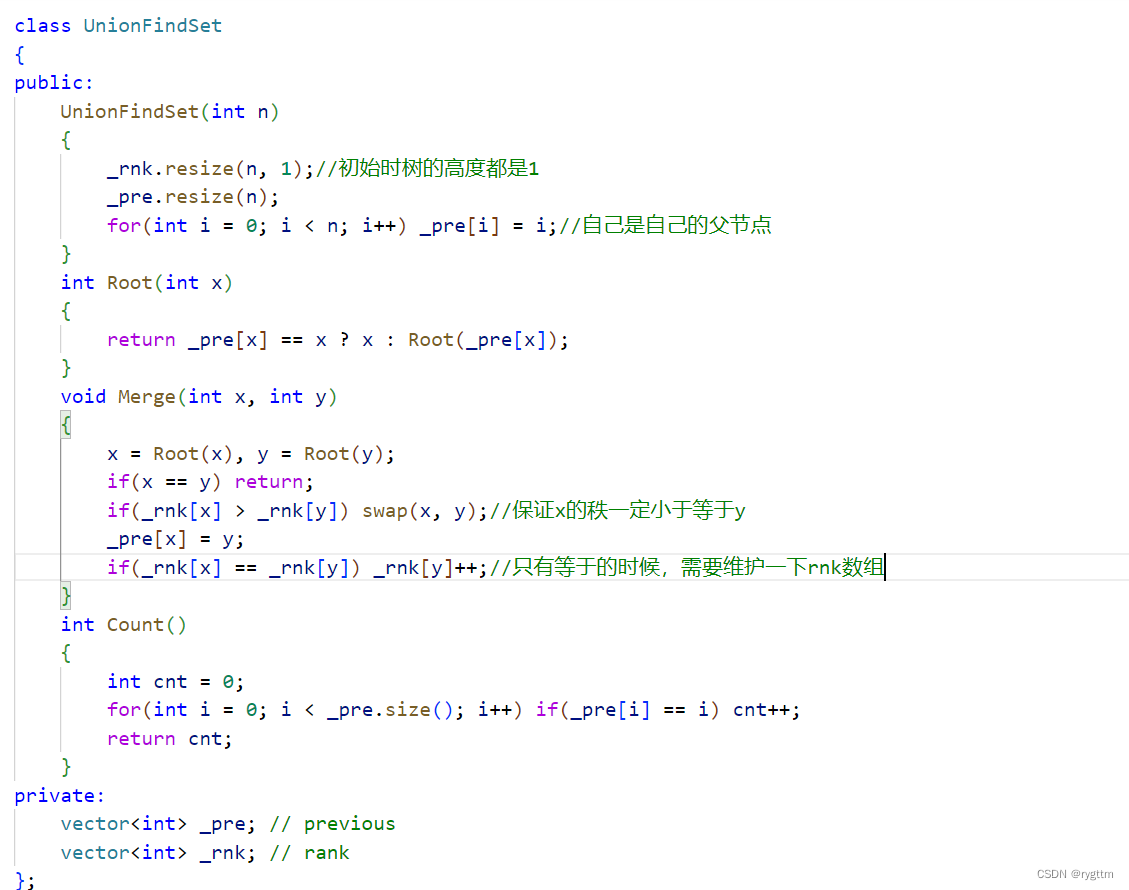
4.启发式合并
启发式合并与按秩合并较为相似,只不过启发式合并是按照树中节点个数的多少来合并的,在合并时尽量让节点个数较少的树合并到节点个数较多的树上,这种优化方式的时间复杂度和按秩合并是近似的,都是O(logN)。如何维护树的节点个数大小呢?只需要维护一个sz数组即可。
这两种方式虽然没有路径压缩那么优秀,但其实在oj里面从消耗时间上来看,其实三种优化方式都是差不多的,因为题目所给数据构成的树可能不是很高,所以O(logN)渐进于O(1)
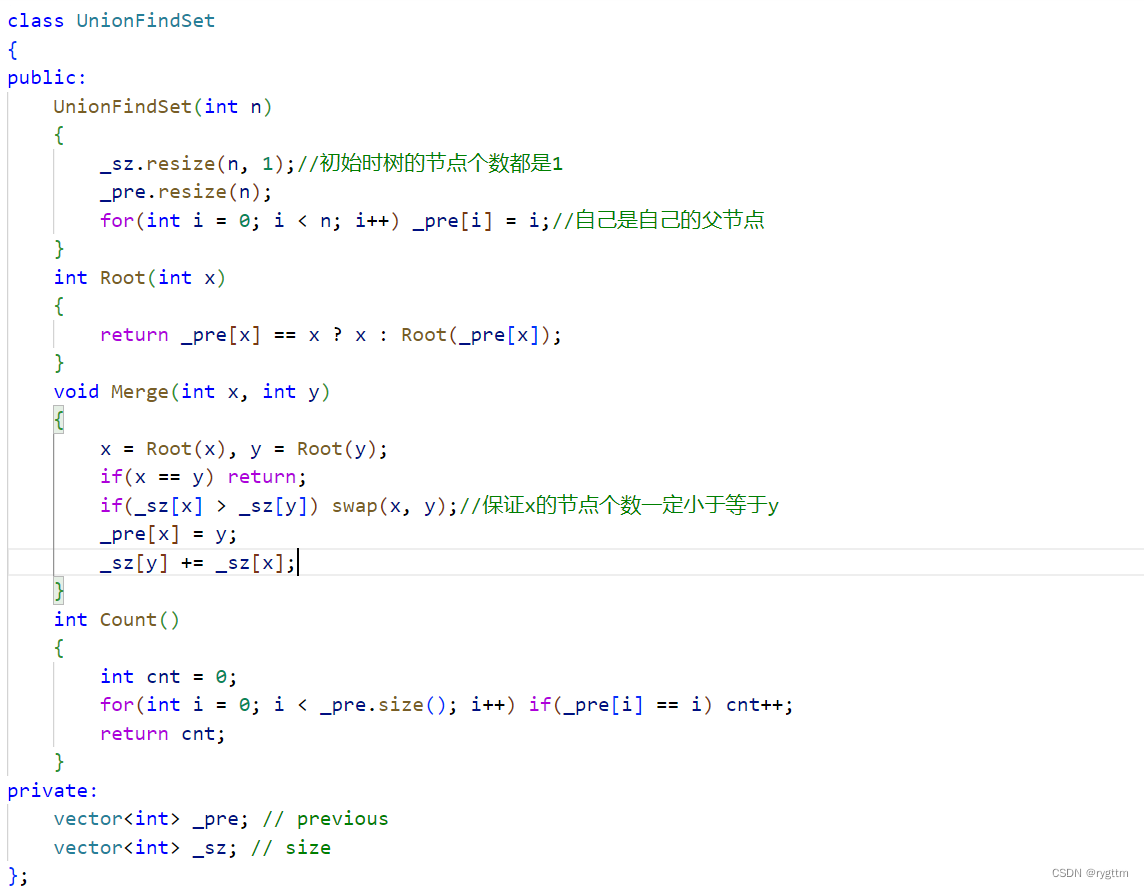
5.练习题
547.省份数量
该题给出了邻接矩阵,我们只需要遍历上半部分,将相连的城市合并到一个连通块当中,最后统计并查集中连通块的总数即为省份的数量。
压缩路径,按秩合并,启发式合并,在下面这道题中你都可以试试,优化效果还是很明显的
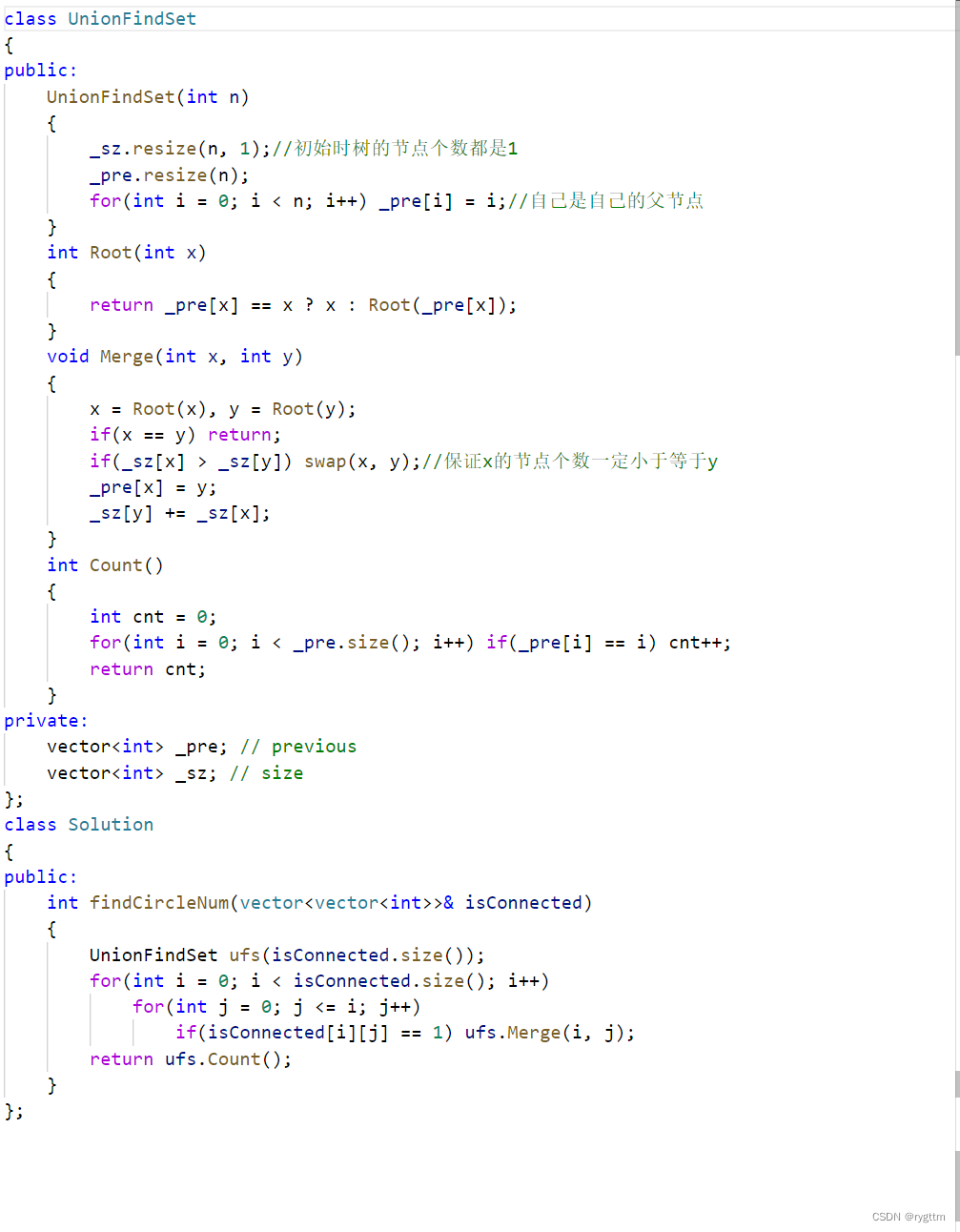
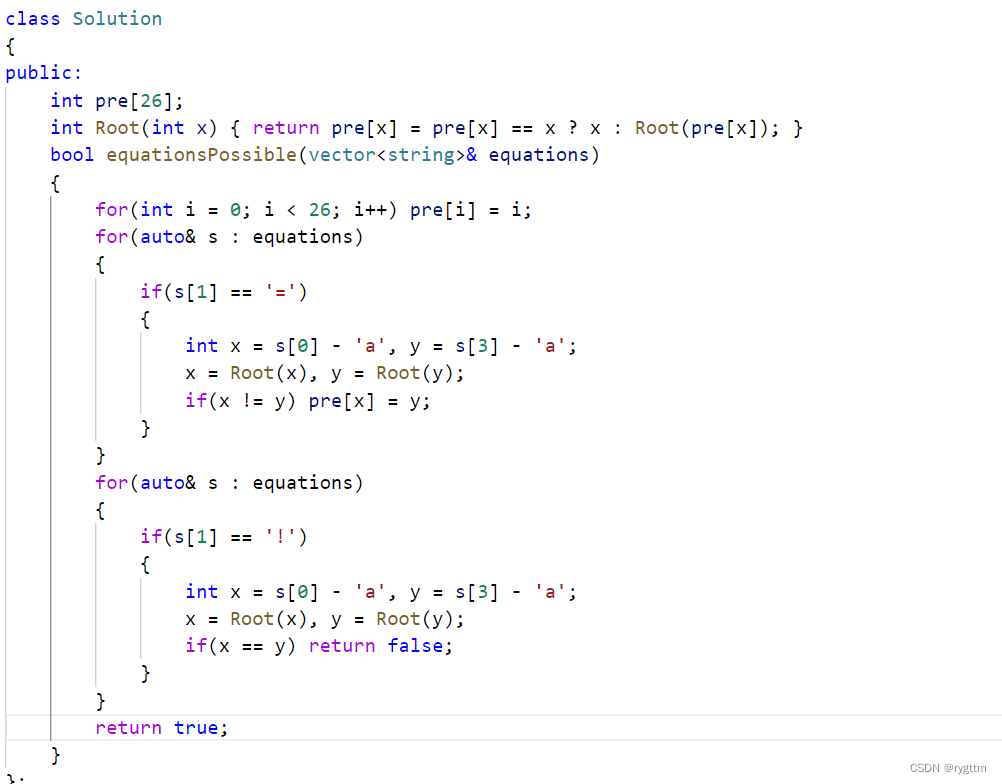
990.等式方程的可满足性
为了让代码看起来优雅一些,用了递归的写法,但时间复杂度不太理想,可能因为栈调用太深了,栈的建立和销毁也耗费了大部分时间,我用循环版的压缩路径试过,3ms即可AC,效果还是比较理想的