前头从来没用过ncc,基于形状匹配搞定后,又翻了翻learning opencv,他并不推荐ncc,而是力推emd,这也是当初我没考虑用ncc的原因。
当初看到ncc公式很复杂,也就忘了。
我的第一个匹配,是最笨的,花了好几秒才有结果,就是模板在图像中实实在在的足行足列找。
后来改进了一下,模板中使用隔行隔列,速度有所上升,但还是慢。
这也是我估计ncc慢的原因。
但opencv有出彩的地方,我一直记不住,就是利用直方图,进行ncc匹配。
闲来无事,研究一下ncc,他的匹配原理是概率论里的相关性。
我们定义,学习模板和图像中任意一个和模板宽高相同的扣图是两个变量的函数,即,学习模板是变量a的函数,图像中任意一个和模板宽高相同的扣图是变量b的函数。
定义,Z(a,b)是变量a和b的协方差。
定义,D(a)是学习模板的方差,D(b)是图像中任意一个和模板宽高相同的扣图的方差。
那么概率论给出了,变量a和变量b的相关性函数:
p=Z(a,b)/sqrt(D(a)*D(b)),sqrt是平方根的意思。条件是方差不为零。
如果学习模板T里的灰度全为零D(a)=0,或者图像中任意一个和模板宽高相同的扣图S灰度全为零D(b)=0,则分母为零,就会异常。
p=1,变量a和b线性相关,我们称为模板T和S匹配。p=0,则变量a和b不相关,模板T和S匹配不匹配。1>=p>0,就是匹配得分情况。
变量a和b不相关,即独立,独立p=0。书中给出了证明:我抄下来了:
协方差=期望(a-期望a)(b-期望b),因为独立,所以
协方差=期望(a-期望a)期望(b-期望b),因为期望(a-期望a)=0,期望(b-期望b)=0,所以
p=Z(a,b)/sqrt(D(a)*D(b))=0/sqrt(D(a)*D(b))=0,证毕
若线性相关(隐含了缩放也可匹配),即a=c*b+x,表示a和b是线性关系。p=1如何证明?我学着证明了一下:
协方差=期望(a-期望a)(b-期望b)=E(a-Ea)(b-Eb)=E(c*b+x-E(c*b+x))(b-Eb)
=E(c*b+x-E(c*b)-x)(b-Eb)==E(c*b-E(c*b))(b-Eb)=c*E(b-Eb)(b-Eb)
而E(b-Eb)(b-Eb)就是b的方差=D(b)
p=Z(a,b)/sqrt(D(a)*D(b))=c*E(b-Eb)(b-Eb)/sqrt(D(a)*D(b))=c*D(b)/sqrt(D(a)*D(b))
因为d(a)=期望(a-期望a)(a-期望a)=E(a-Ea)(a-Ea)
=E(c*b+x-E(c*b+x))(c*b+x-E(c*b+x))
=c*c*E(b-Eb)(b-Eb)=c*c*D(b)
所以:p=c*D(b)/sqrt(D(a)*D(b))中D(a)被上面公式替换,
p=c*D(b)/sqrt(c*c*D(b)*D(b))=c*D(b)/(c*D(b))=1
证毕。
下面是验证灰度ncc匹配的c#代码:
//下面比对学习到的roiImage备用ncc和匹配到的roiImage备用ncc2两幅图像
// 下面使用灰度法ncc202402011731
// 没有考虑旋转
double 学习凸包的中心x = 0;
double pipei凸包的中心x = 0;
for (int i = 0; i < roiwforncc * roihforncc; i++)
{
学习凸包的中心x += roiImage备用ncc[i];
pipei凸包的中心x += roiImage备用ncc2[i];
}
学习凸包的中心x = 学习凸包的中心x /(roiwforncc * roihforncc);
pipei凸包的中心x = pipei凸包的中心x / (roiwforncc * roihforncc);
double aa = 0;
double bb = 0;
double cc = 0;
for (int i = 0; i < roiwforncc * roihforncc; i++)
{
aa += (roiImage备用ncc[i] - 学习凸包的中心x) * (roiImage备用ncc2[i] - pipei凸包的中心x);
bb += (roiImage备用ncc[i] - 学习凸包的中心x) * (roiImage备用ncc[i] - 学习凸包的中心x);
cc += (roiImage备用ncc2[i] - pipei凸包的中心x) * (roiImage备用ncc2[i] - pipei凸包的中心x);
}
double p = 0;
p = aa / Math.Sqrt(bb * cc);
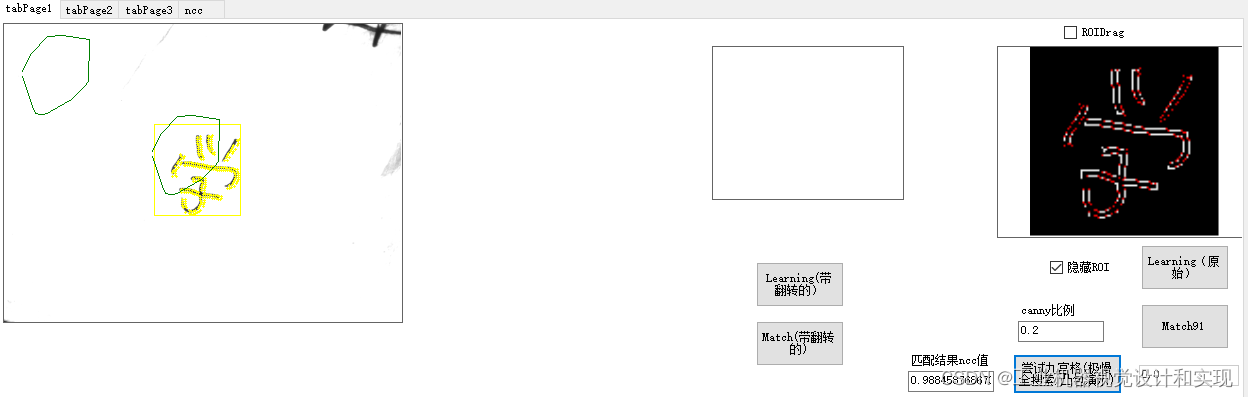
下一篇给出验证前面直方图梯度角度(hog)的ncc代码,补充ncc对旋转的不足。
opencv中的直方图ncc就不验证了,公式有,自己写一下。

![[BUUCTF]-PWN:picoctf_2018_can_you_gets_me解析](https://img-blog.csdnimg.cn/direct/0a92644371b5477998df997e60ab5d8d.png)