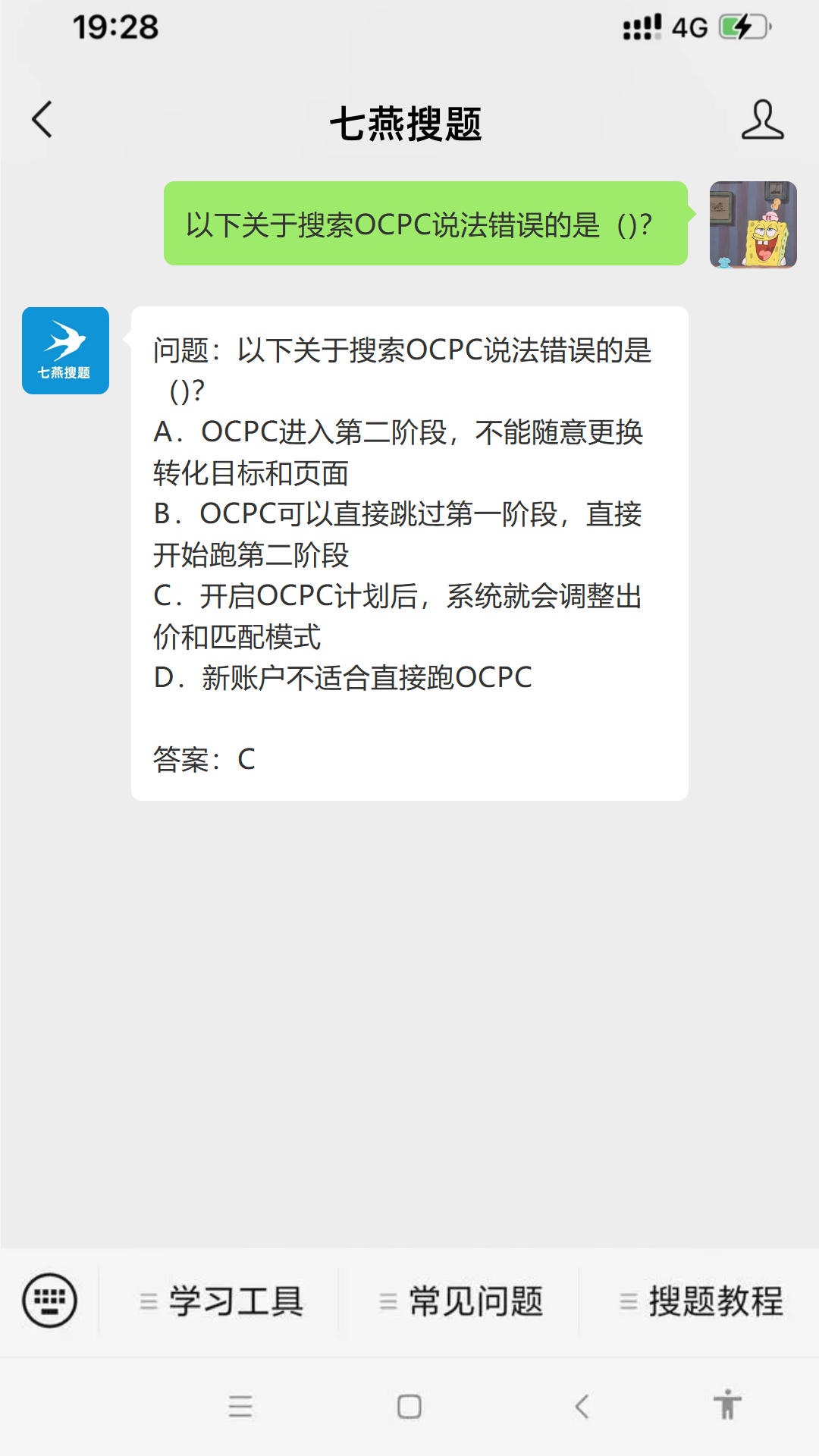
本题的难点其实不在思路上，而是有些人遇到这种题就不想做了，题目太长，有点读不懂题。

只要先耐心下来把题读懂之后这题其实就没那么难了，读懂题之后还有一个关键点就是，我们怎么在1e8时间复杂度之内跑过呢？这个是我们的重难点，我们分析一下500*500的长宽的话，最少需要枚举多少个9宫格，我们以每个点为左上角的点进行枚举，大概需要枚举((500 - 3) + 1) * (500 - 3) + 1)）个，这其实是有公式的，就是那个500都是n，m,那么我们最多只需要枚举250000个九宫格，然后判断一下这些九宫格是否符合要求小于或等于threodsold，这是2250000的复杂度，符合要求之后，我们再进行对九宫格求和求平均值，5500000的复杂度，如果想要更快速的话，可以用二维前缀和优化对九宫格求和这部分，但是赛时我就不求二维前缀和了，直接用这个就行，然后我们现在还有一个要求没有达到，那就是如何求多个区域的平均值，那么就需要记录每个区域在该坐标的平均值是多少，这个部分不会复杂度很高，最多有9个平均值，所以这个不用管。那么有了这些条件我们就可以过这题了，就是个大模拟的题

class Solution {
public:vector<int> val[511][511];int dx[4] = {0,-1,0,1};int dy[4] = {-1,0,1,0};vector<vector<int>> resultGrid(vector<vector<int>>& image, int threshold) {memset(val,0,sizeof(val));int n = image.size();int m = image[0].size();vector<vector<int>> ans(n,vector<int>(m,0));for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){int left_x = i,left_y = j;int right_x = i + 2,right_y = j + 2;if(right_x >= n || right_y >= m) continue;bool flag = false;for(int x = left_x;x <= right_x;x++){for(int y = left_y;y <= right_y;y++){for(int k = 0;k < 4;k++){int a = dx[k] + x,b = dy[k] + y;if(a < left_x || a > right_x || b < left_y || b > right_y) continue;if(abs(image[x][y] - image[a][b]) > threshold) {flag = true;}}}}int sum = 0;if(!flag){for(int x = left_x;x <= right_x;x++){for(int y = left_y;y <= right_y;y++){sum += image[x][y];}}//out<<sum<<endl;int aveg = sum / 9;for(int x = left_x;x <= right_x;x++){for(int y = left_y;y <= right_y;y++){val[x][y].push_back(aveg);}}}}}a:for(int i = 0;i < n;i++){for(int j = 0;j < m;j++){int sum = 0;for(auto&e:val[i][j]) sum += e;int len = val[i][j].size();if(len){//cout<<sum<<endl;int aveg = sum / len;ans[i][j] = aveg;}else ans[i][j] = image[i][j];}}return ans;}
};