题目

---

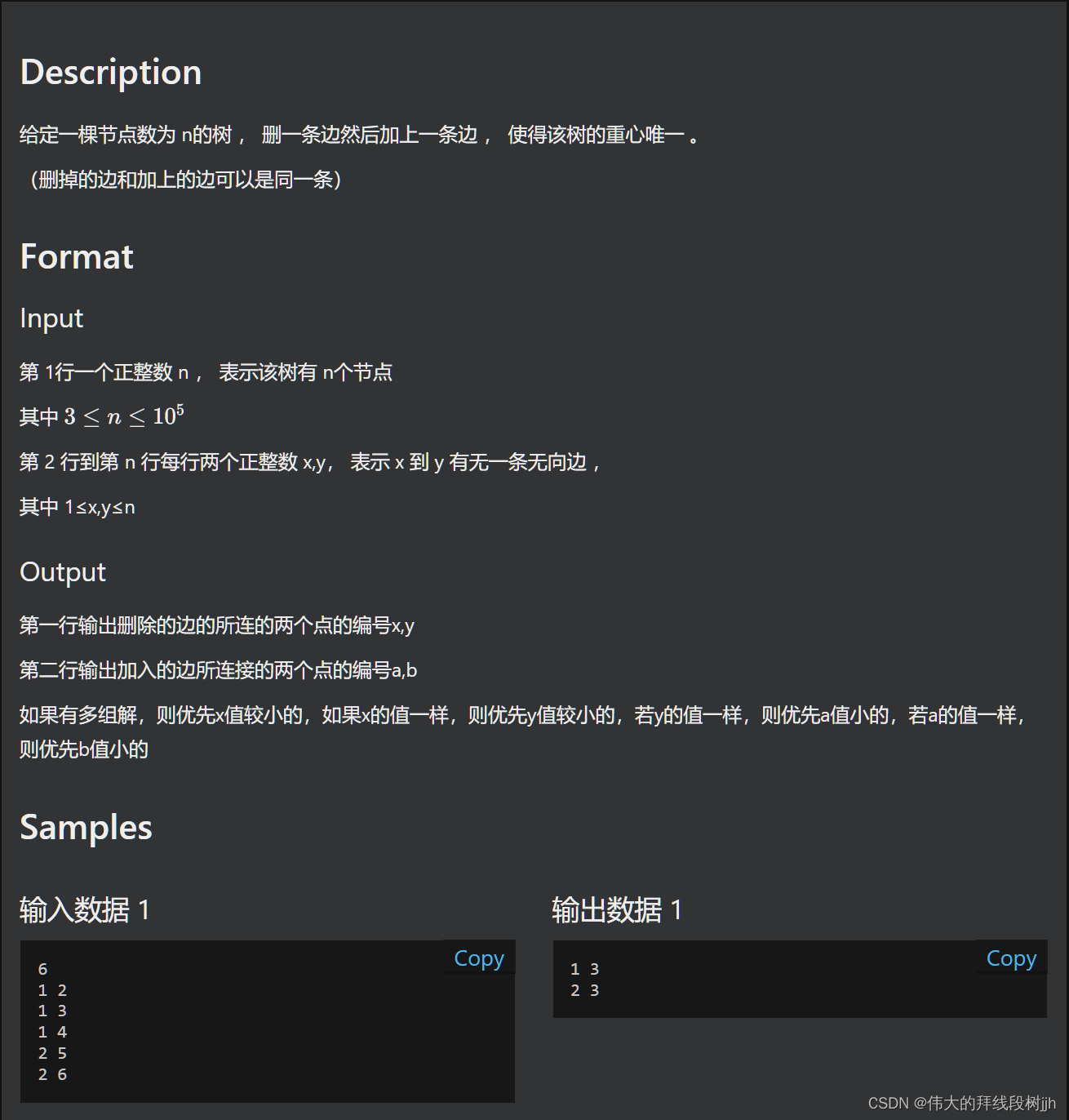
思路

分类讨论。

首先当树只有一个重心的时候,我们删掉最小的边再加上原边即可.

再看有两个重心的情况.

显然这棵树必定是类似这样的:

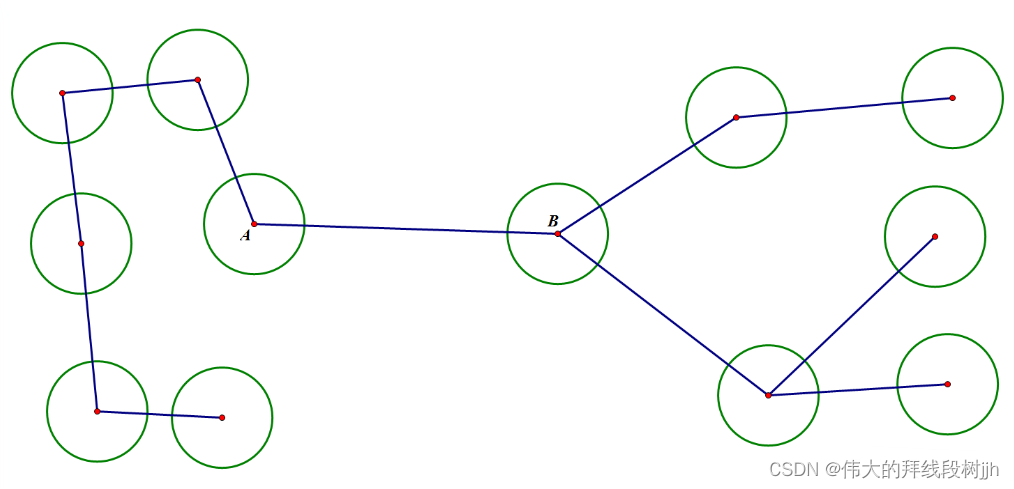
即删掉 A 后,以B 为根的子树是剩下的最大连通块,反之亦然.

那就可以得到一个结论:

• 删掉边 (A,B) 后,两棵树的大小相等.

那我们只要使两棵树的大小不相等,且不使新的点成为重心即可.

那就考虑直接从A 树中取一位编号最小叶子节点,把这个节点与它父亲的边断开,连到 B 的直接儿子中编号最小的节点上去.

这样, A 树的大小变小了,而 B 树的大小变大了,且不会有新的节点成为重心.

那 A 就不再是重心了,而 B 则成为了唯一的重心.

 代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
struct ff
{int u,v;
};
ff b[100001];
int n,v[100001],zjd[100001],a[1000001],ans = 1e9,zhong,mnzi = 1e9,mnfa,tzhong,ttzhong,lz,t = 1e9,tt = 1e9;//zjd[x]代表以x为根的子树中最大的子树有多少节点
//v[x]代表 以x为根的子树一共有多少节点
vector<int> vec[300001];
int dfs(int k,int fa)//求树的重心
{int sum = 1;bool b = 1;for(int i:vec[k])if(i != fa){int u = dfs(i,k);if(u > n / 2) b = 0;sum += u;}if(n - sum - 1 >= n / 2) b = 0;if(b) a[++zhong] = k;return sum;
}
void dfs_2(int x,int fa,int p)
{if(p == 1 && x == tzhong) return ;if(p == 0 && x == ttzhong) return ;if(x < mnzi && fa != 0){mnzi = x;mnfa = fa;lz = p;}if(p == 0 && t > x) t = x;if(p == 1 && tt > x) tt = x;for(int i = 0; i < vec[x].size(); i++)if(fa != vec[x][i])dfs_2(vec[x][i],x,p);
}
bool cmp(ff x,ff y)
{if(x.u != y.u) return x.u < y.u;return x.v < y.v;
}
signed main()
{cin>>n;for(int i = 1; i < n; i++){int u,v;cin>>u>>v;vec[u].push_back(v);vec[v].push_back(u);b[i].u = min(u,v);b[i].v = max(u,v);}sort(b + 1,b + n,cmp);dfs(1,0);tzhong = a[1];ttzhong = a[2];if(zhong == 1){sort(vec[a[1]].begin(),vec[a[1]].end());cout<<a[1]<<' '<<vec[a[1]][0]<<'\n'<<a[1]<<' '<<vec[a[1]][0];}else{dfs_2(tzhong,0,0);dfs_2(ttzhong,0,1);cout<<min(mnzi,mnfa)<<' '<<max(mnzi,mnfa)<<endl;if(lz == 0) cout<<min(tt,mnzi)<<' '<<max(tt,mnzi);else cout<<min(t,mnzi)<<' '<<max(t,mnzi);}return 0;
}