1、101. 对称二叉树
检查是否对称,其实就是检查左节点等不等于右节点,我们可以用递归来做。
如果左右节点都为null,说明肯定对称呀,返回true。
如果一个为null一个不为null,或者左右的值不相等,则为false。(这里简化一下,比如
left==null&&right!=null可以只写left==null,因为如果都为null,会进入第一个if)。
如果两个值相等,不代表一定对称,还需要继续检查左节点的左节点和右节点的右节点、左节点的右节点和右节点的左节点是否相等。
class Solution {public boolean isSymmetric(TreeNode root) {return check(root.left, root.right);}boolean check(TreeNode left, TreeNode right){if(left == null && right == null){return true;}if(left == null || right == null || left.val != right.val){return false;}return check(left.left, right.right) && check(left.right, right.left);}
}2、104. 二叉树的最大深度
递归解法
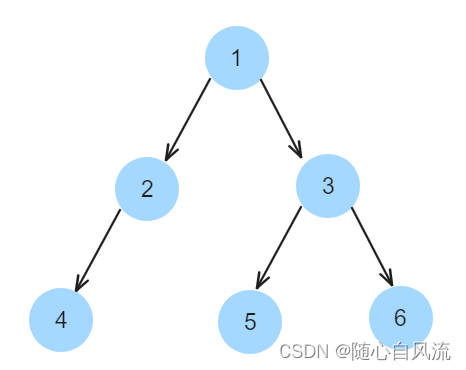
要求这棵树的最大深度,我们只需要求左子树和右子树的深度,然后取最大值加一就好,同样地对每个节点都如此,于是就可以用递归来解。
class Solution {public int maxDepth(TreeNode root) {if(root == null){return 0;}if(root.left == null && root.right == null){return 1;}return Math.max(maxDepth(root.left), maxDepth(root.right))+1;}
}迭代解法
这个解法实际上就是改造一下非递归后序遍历的代码,因为每次遍历都会将节点入栈,我们只需要在弹栈之前,记录一下栈的大小,取最大值就好。
class Solution {public int maxDepth(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();TreeNode pop = null;int ans = 0;while(root != null || !stack.isEmpty()){if(root != null){stack.push(root);root = root.left;}else{ans = Math.max(ans, stack.size());TreeNode peek = stack.peek();if(peek.right == null || peek.right == pop){pop = stack.pop();}else{root = peek.right;}}}return ans;}
}3、111. 二叉树的最小深度
递归解法
一开始我想着和第2题一个思路,结果发现这样不行。比如这种退化成链表的树
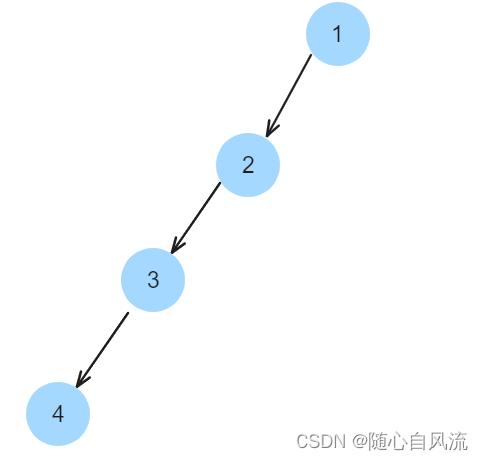
如果直接套用最大深度的代码,会返回1
所以我们需要判断一下,如果左子树深度是0,那么就返回右子树+1的深度,对于右子树同理。
class Solution {public int minDepth(TreeNode root) {if(root == null) return 0;if(root.left == null && root.right == null) return 1;int left = minDepth(root.left);int right = minDepth(root.right);if(left == 0) return right+1;else if(right == 0) return left+1;else return Math.min(left, right) + 1; }
}
层序遍历
最大深度也可以用层序遍历来写,因为层序遍历就是遍历每一层嘛,最大深度就遍历到最后一层,最小深度就遍历到第一个叶子节点就好了。
我们用队列来实现,每次拓展结点的时候都检查一下是否有左右节点,如果都没有,就可以返回层数了。
class Solution {public int minDepth(TreeNode root) {if(root == null) return 0;LinkedList<TreeNode> q = new LinkedList<>();int cnt = 0;q.offer(root);while(!q.isEmpty()){cnt++;int len = q.size();for(int i = 0; i < len; i++){boolean f = true;TreeNode t = q.poll();if(t.left != null){q.offer(t.left);f = false;}if(t.right != null){q.offer(t.right);f = false;}if(f) return cnt;}}return cnt;}
}4、 226. 翻转二叉树
举个例子,如果要翻转如下的树:
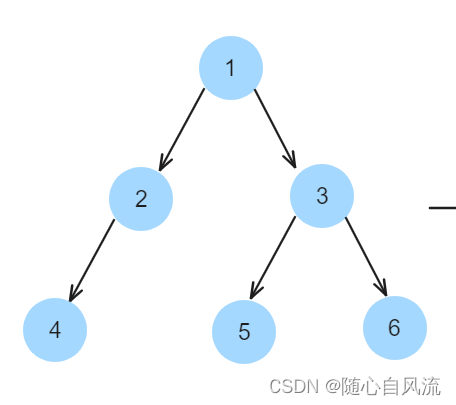
先交换2、3:

然后交换3的孩子节点、2的孩子节点
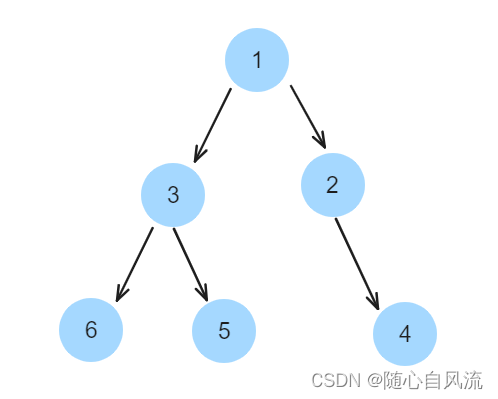
每一步的操作都是一样的,于是我们就能用递归解决。
class Solution {public TreeNode invertTree(TreeNode root) {invert(root);return root;}void invert(TreeNode node){if(node == null) return;TreeNode t = node.left;node.left = node.right;node.right = t;invert(node.left);invert(node.right);}
}