目录
Leetcode 39. 组合总和
Leetcode 40.组合总和II
Leetcode 131.分割回文串
Leetcode 39. 组合总和
题目链接:Leetcode 39. 组合总和
题目描述:给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
思路:因为这是一道组合问题,因此可以想到用回溯算法。
代码如下:
这里需要注意的是可以无限重复选取,因此递归过程中不能像之前一样传入i+1,而需要传入i。
class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int start) {if (sum > target)return;if (sum == target) {result.push_back(path);return;}for (int i = start; i < candidates.size(); i++) {sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i);//这里不用i+1的原因是因为可以读取相同元素//回溯sum -= candidates[i];path.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtracking(candidates, target, 0, 0);return result;}
};- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(target)
Leetcode 40.组合总和II
题目链接:Leetcode 40.组合总和II
题目描述:给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。解集不能包含重复的组合。
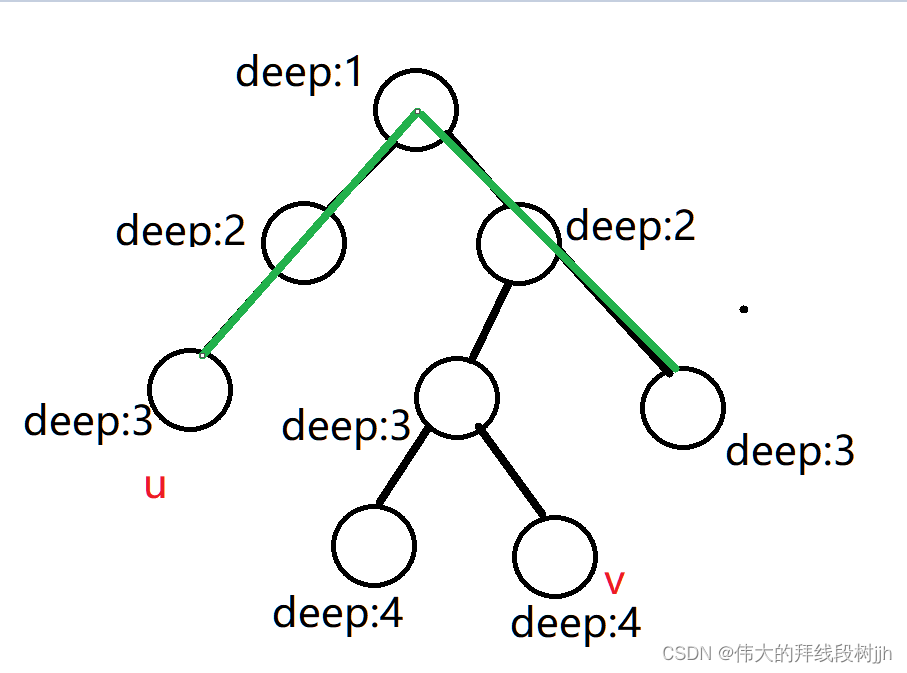
思路:本题和上道题类似,也是组合问题,只不过上道题可以选重复元素,本题不能重复选取使用过的元素。注意:我们要去重的是同一树层上的“使用过”,同一树枝上的都是一个组合里的元素,不用去重,并且需要将数组提前排序。

注,以上图片来源于《代码随想录》
代码如下:
class Solution {
public:vector<vector<int>> result;vector<int> path;void backtracking(vector<int>& candidates, int target, int sum, int start) {if (sum > target)return;if (sum == target) {result.push_back(path);return;}for (int i = start; i < candidates.size(); i++) {//去重if (i > start && candidates[i] == candidates[i - 1]) {continue;}sum += candidates[i];path.push_back(candidates[i]);backtracking(candidates, target, sum, i + 1);sum -= candidates[i];path.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());//只有排序之后才可以让相同元素挨在一起backtracking(candidates, target, 0, 0);return result;}
};- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n)
Leetcode 131.分割回文串
题目链接:Leetcode 131.分割回文串
题目描述:给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。回文串是正着读和反着读都一样的字符串。
思路:本题属于切割问题,因此也可以使用回溯算法;同时需要判断回文串,这个可以使用双指针法判断。对回溯算法的使用范围不太了解的可以看这里
代码如下:(回溯)
class Solution {
public:vector<vector<string>> result;vector<string> path;//判断是否是回文串bool isPalindrome(const string& s, int start, int end) { //双指针法for (int i = start, j = end; i < j; i++, j--) {if (s[i] !=s[j]) {return false;}}return true;}void backtracking(const string& s, int start) {if (start >= s.size()) {result.push_back(path);return;}for (int i = start; i < s.size(); i++) {if (isPalindrome(s, start, i)) {//获取[start,i]的子串string str = s.substr(start, i - start + 1);path.push_back(str);} else {continue;}backtracking(s, i + 1); //不能重复寻找path.pop_back(); //回溯}}vector<vector<string>> partition(string s) {backtracking(s, 0);return result;}
};- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n^2)
当然也可以利用动态规划不需要每次利用双指针重复判断。
代码如下:(回溯+动态规划优化)
class Solution {
private:vector<vector<string>> result;vector<string> path; // 放已经回文的子串vector<vector<bool>> isPalindrome; // 放事先计算好的是否回文子串的结果void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {if (isPalindrome[startIndex][i]) { // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else { // 不是回文,跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程,弹出本次已经添加的子串}}void computePalindrome(const string& s) {// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串 isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小for (int i = s.size() - 1; i >= 0; i--) { // 需要倒序计算, 保证在i行时, i+1行已经计算好了for (int j = i; j < s.size(); j++) {if (j == i) {isPalindrome[i][j] = true;}else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}}}}
public:vector<vector<string>> partition(string s) {result.clear();path.clear();computePalindrome(s);backtracking(s, 0);return result;}
};总结:感觉回溯算法很好理解hhh,不过最后一道题利用动态规划优化这块还是不太好想。
最后,如果文章有错误,请在评论区或私信指出,让我们共同进步!