首先，我们得分清楚子序列和子串的区别：
1、最长子串是指在字符串中连续的一段最长的字符串
2、最长子序列是指在字符串中不一定连续的最长字符串
了解到这两个概念之后我们来看一个比较基础的最长子序列问题，此处以蓝桥杯练习题第一题为例：题库 - 蓝桥云课 (lanqiao.cn)
https://www.lanqiao.cn/problems/?first_category_id=1&second_category_id=8&sort=difficulty&asc=1
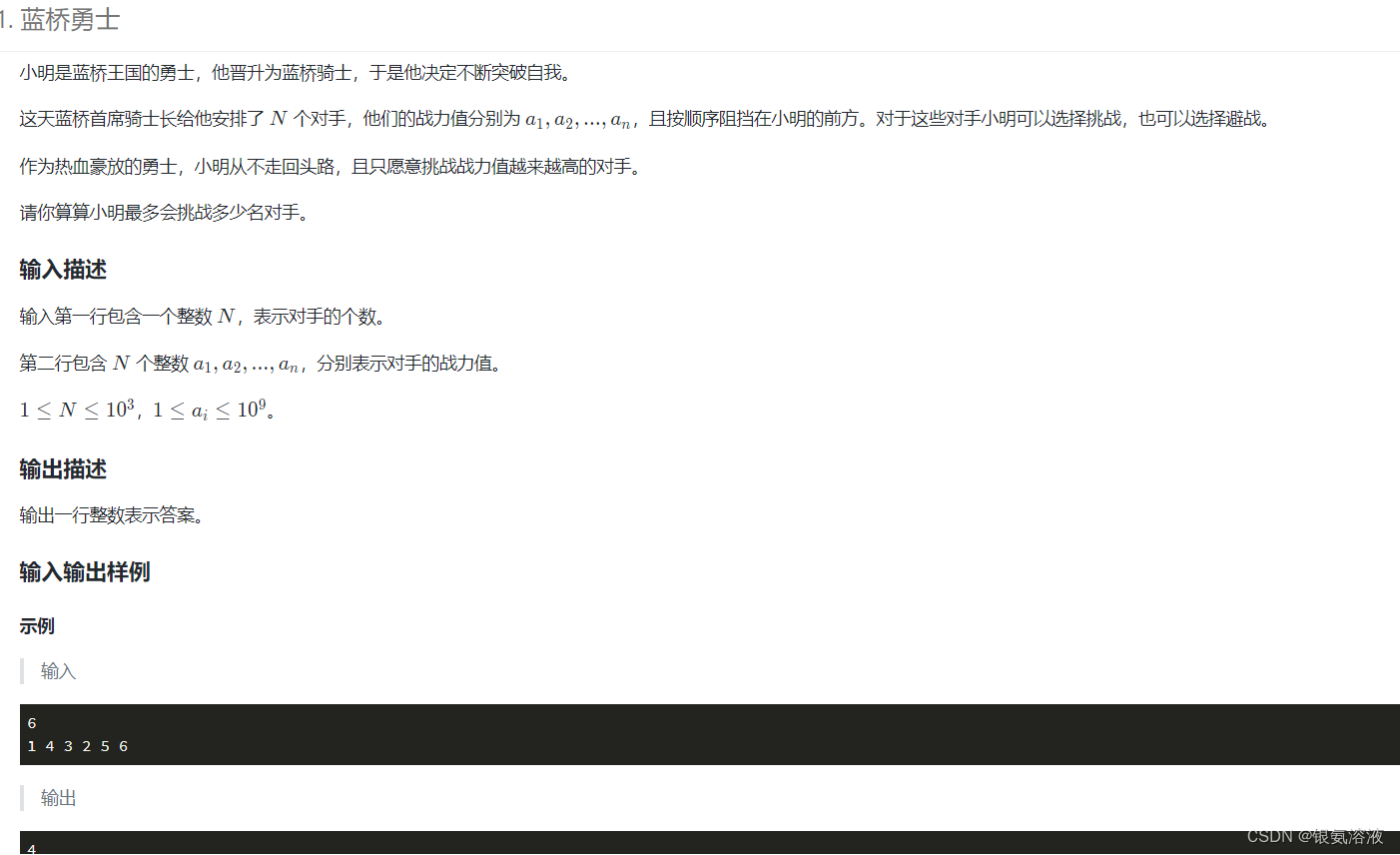
那接下来我们先看代码吧：
#include <bits/stdc++.h>
using namespace std;
int a[1001],dp[1001];//dp[i]表示存放当前位之前最大的子序列
int main()
{
int n,temp;
cin>>n;
for(int i=1;i<=n;i++){cin>>a[i];dp[i]=1;//将初始值设置为1
}
for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){//遍历i以及i之前的最长子序列if(a[i]>a[j]){//如果当前值小于i值，则判断当前值的子序列长度dp[i]=max(dp[i],dp[j]+1);//当前值的子序列长度+1和i值子序列大小作比较}}
}
int re=0;
for(int i=1;i<=n;i++)
re=max(re,dp[i]);//找到子序列中最大子序列
cout<<re;return 0;
}分析此题，我们可以设数组dp[i]表示以 a[i] 这个数结尾的最⻓递增⼦序列的⻓度。且dp[i] 初始值为 1，因为以 a[i] 结尾的最⻓递增⼦序列起码要包含它⾃⼰。
那如何来求dp数组呢？
假设dp[0....n-1]我们都知道(针对此题dp[1]=1,dp[2]=2,dp[3]=2,dp[4]=2,dp[5]=3)，那接下来求dp[n]，针对此题我们只要找到前⾯那些结尾⽐ 6⼩的⼦序列，然后把 6 接到这些⼦序列末尾，就可以形成⼀个新的递增⼦序列，⽽且这个新的⼦序列⻓度加⼀，即dp[6]=dp[5]+1，此处的+1表示加上dp[6]本身。
知道了如何求dp[6]，其实求dp[0....n-1]也就不难了，即以下代码为求dp数组：
for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){//遍历i以及i之前的最长子序列if(a[i]>a[j]){//如果当前值小于i值，则判断当前值的子序列长度dp[i]=max(dp[i],dp[j]+1);//当前值的子序列长度+1和i值子序列大小作比较}}
}以上便是简单地最长子序列求解方式，以下提供几道题供读者练习：
P8697 [蓝桥杯 2019 国 C] 最长子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
B3637 最长上升子序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
354. 俄罗斯套娃信封问题 - 力扣（LeetCode）
