题意

给定一个整数 n ，返回 n! 结果中尾随零的数量。提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1

//题解
class Solution {
public:int trailingZeroes(int n) {
// ...*(1*5)*...*(x*5)*...*(1*5*5)*...*(x*5*5)*...*n 然后倒过来    	//...∗(1∗5)∗...∗(1∗5∗5∗5)∗...∗(2∗5∗5∗5)∗...∗(3∗5∗5∗5)∗...∗nreturn n == 0 ? 0 : n / 5 + trailingZeroes(n / 5);}
};

已经有热线网友 给了白话 题解过程
我们先以n=7举个例子，看一下7!7!7!末尾有几个0。我们把7!7!7!展开来看下：7!=1∗2∗3∗4∗5∗6∗77! = 1 * 2 * 3 * 4 * 5 * 6 * 7
7!=1∗2∗3∗4∗5∗6∗7
我们知道，只有2∗52*52∗5才可以得到一个000，那我们只需要看7!7!7!可以分解为多少个2∗52*52∗5就可以。222出现的频率肯定是高于555的，因为:每隔 2 个数就会包含因子222，比如2,4,6,..2,4,6,..2,4,6,..，
而每个 5 个数才会出现一个包含因子555的数，比如5,10,15,..5,10,15,..5,10,15,..
那我们的题目就可以转换为，n!n!n!最多可以分解出多少个因子555。对于n!n!n!，5 的因子一定是每隔 5 个数出现一次，也就是下边的样子。n!=1∗2∗3∗4∗(1∗5)∗...∗(2∗5)∗...∗(3∗5)∗...∗nn! = 1 * 2 * 3 * 4 * (1 * 5) * ... * (2 * 5) * ... * (3 * 5) *... * n
n!=1∗2∗3∗4∗(1∗5)∗...∗(2∗5)∗...∗(3∗5)∗...∗n
但我们还会发现，每隔 25(5*5) 个数字，出现的是 2 个 5，如下：...∗(1∗5)∗...∗(1∗5∗5)∗...∗(2∗5∗5)∗...∗(3∗5∗5)∗...∗n... * (1 * 5) * ... * (1 * 5 * 5) * ... * (2 * 5 * 5) * ... * (3 * 5 * 5) * ... * n
...∗(1∗5)∗...∗(1∗5∗5)∗...∗(2∗5∗5)∗...∗(3∗5∗5)∗...∗n
比如1∗5∗51*5*51∗5∗5，2∗5∗52*5*52∗5∗5，里面包含了 2 个 5。同理，每隔 125(5*5*5)个数字，出现的是 3 个 5，如下:...∗(1∗5)∗...∗(1∗5∗5∗5)∗...∗(2∗5∗5∗5)∗...∗(3∗5∗5∗5)∗...∗n... * (1 * 5) * ... * (1 * 5 * 5 * 5) * ... * (2 * 5 * 5 * 5) * ... * (3 * 5 * 5 * 5) * ... * n
...∗(1∗5)∗...∗(1∗5∗5∗5)∗...∗(2∗5∗5∗5)∗...∗(3∗5∗5∗5)∗...∗n
那么，我们要计算n!中一共有多少个因子5的话，计算方法方式就应该是：每隔5个数出现一次的因子5的次数+每隔25个数出现一次的因子5的次数+...每隔5个数出现一次的因子5的次数 + 每隔25个数出现一次的因子5的次数 + ...
每隔5个数出现一次的因子5的次数+每隔25个数出现一次的因子5的次数+...
也就是:n/5+n/(5∗5)+n/(5∗5∗5)+...n/5 + n/(5*5) + n/(5*5*5) + ...
n/5+n/(5∗5)+n/(5∗5∗5)+...

碰到一个很有意思的事情

我问GPT ，然后GPT立马就找出阶乘的相关原题
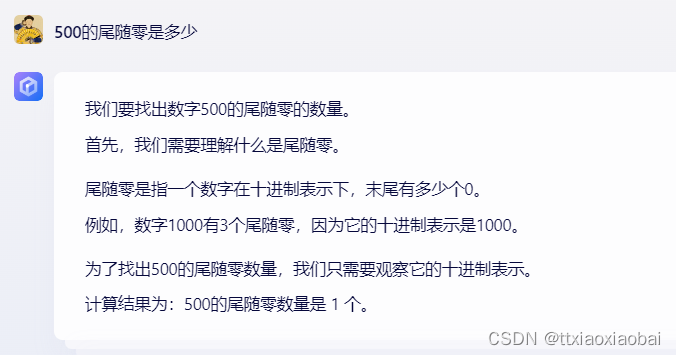
但我在想500 = （25）（2*5）*5
如果不是500阶乘的话，那就只有两个5和仅有的两个2配对，那500的末尾零应该是2

事实上，如果直接上结果，而不给出正确的推导过程，GPT会一直无脑给结果，只有当你给出正确的逻辑推导之后，他会顺着你的思路走，然后形成结果，当你再去测试，这回他变聪明了。

当然测试怎么能忘了百度
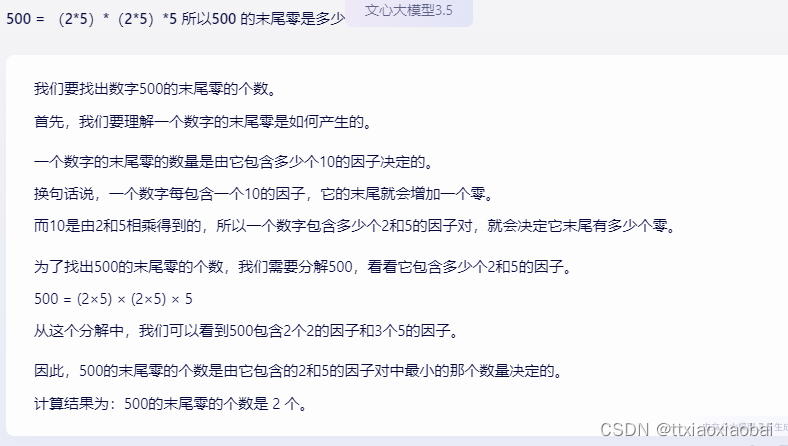
然后就在文心一言上测试

当给出 正确的逻辑过程，百度也学聪明了

后面，再忽悠他，也忽悠不住

总结来说，当只是主观给出一个结论，然后GPT也会给一个主观回复（也就是胡说八道）当，你喂一些正确的逻辑推导过程，他就立马学以致用，然后再去忽悠，也就忽悠不住了。