13 冒泡排序和快速排序-编程知识

1. 冒泡排序

1.1 基本思想

数据中相邻的两数不断比较，找出最大的数进行交换，不断往后相比，找到整个数列中的最值，第二轮找到次值

void BubblingSort(int ary[], int len)
{int flag = 1;for (int i = 0; i < len - 1; i++){for (int j = 0; j < len - i - 1; j++){if (ary[j] > ary[j + 1]){flag = 0;int temp = ary[j];ary[j] = ary[j + 1];ary[j + 1] = temp;}}//未发生交换,原数据有序if (flag == 1){break;}}
}

1.2 特性

1.冒泡排序是一种很容易理解的排序
2.时间复杂度：O(N²)
3.空间复杂度: O(1)
4.稳定性: 稳定

2. 快速排序

2.1 基本思想

快速排序是hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想是：任取某待排序中某元素为基准值，按照排序码将待排序集合分割成左右子序列，左子序列所有元素均小于基准值，右子序列均大于基准值，然后在左右子序列中重复此过程

在这里插入图片描述

快速排序分为子序列分割的方法和调用，，以key值分割左右区间，下面先写出递归左右序列的框架

void Qsort(int ary[], int left, int right)
{//区间错误,返回if (left >= right){return;}int keyi = QSplit(ary, left, right);//递归左右区间,keyi处除外Qsort(ary, left, keyi - 1);Qsort(ary, keyi + 1, right);}

2.1.1 hoare版

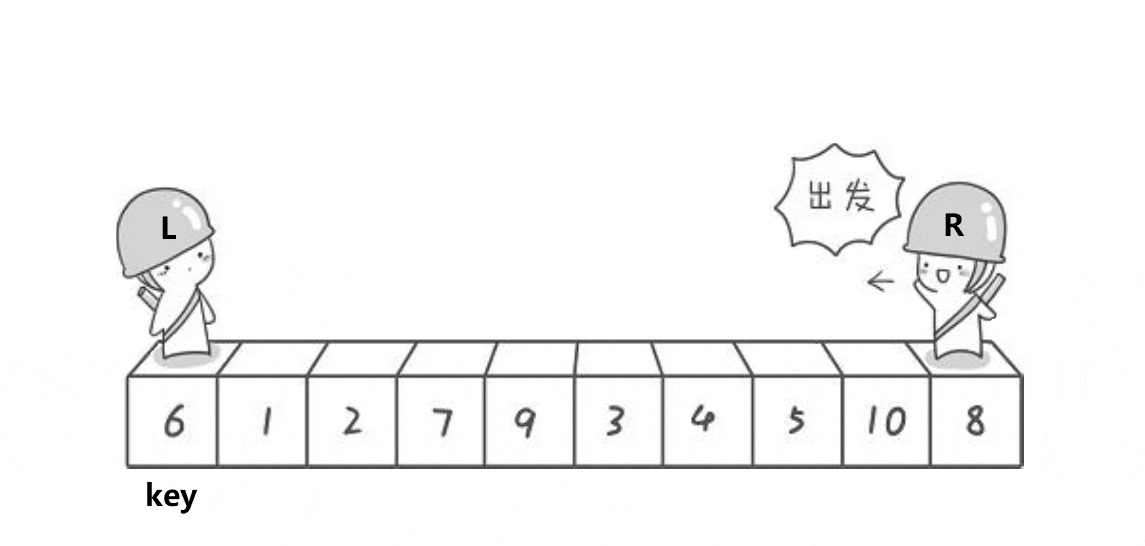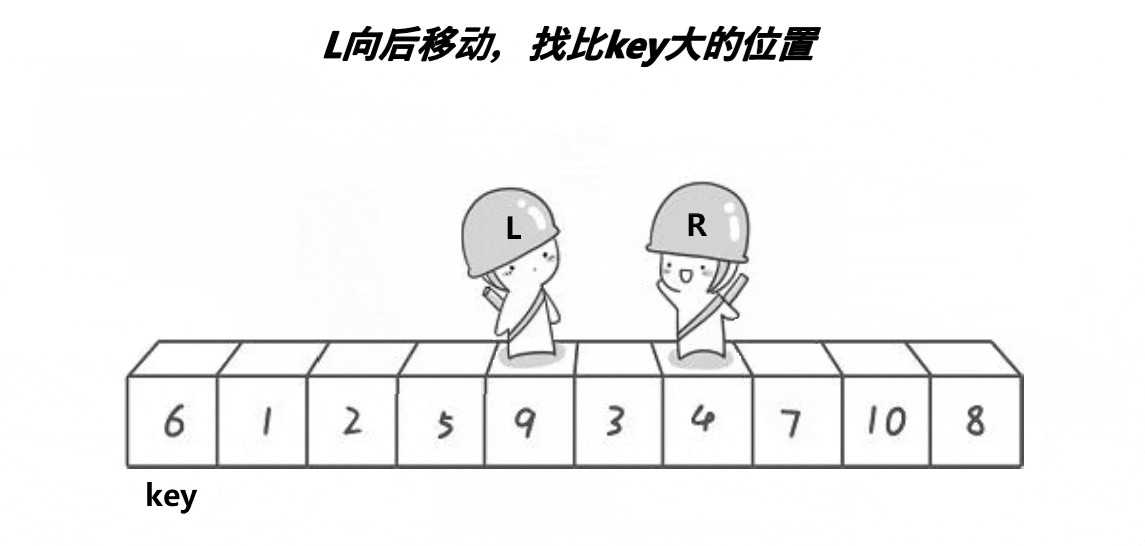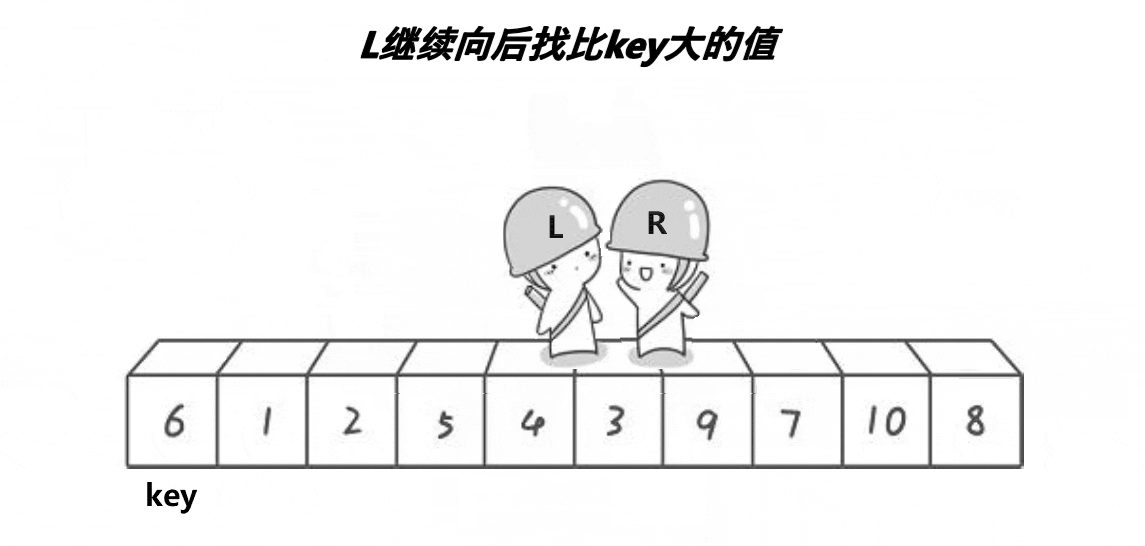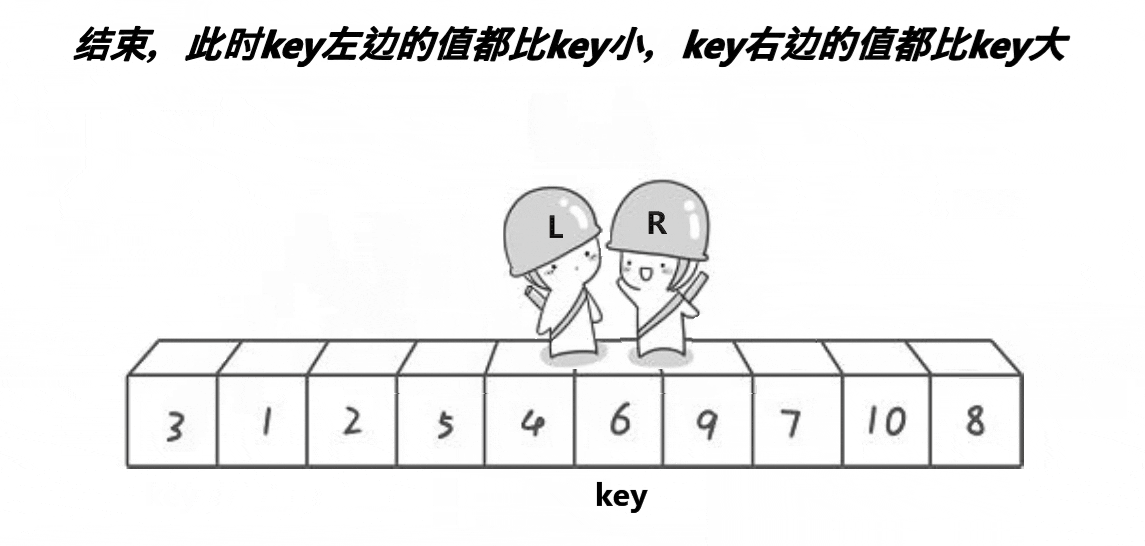
在这里插入图片描述
上面的过程，首先6是key值，R小人往左走，找到比6小的数字停下来。然后L小人往右走，找到比6大的，然后交换两个数。继续走，直到两个小人相遇，就交换key值和相遇位置

根据上述过程写出简单的单趟过程

void QSplit(int ary[], int left, int right)
{int keyi = left;while (left < right){//右边找大while (ary[right] > ary[keyi]){right--;}//左边找小while (ary[left] < ary[keyi]){left++;}Swap(&ary[left], ary[right]);}Swap(&ary[left], &ary[keyi]);
}

上面的代码有三个问题：
死循环
在找大和找小的过程中如果相等也会退出，交换后还是两个相等值，就会不断进入循环
越界
如果寻找的key值是一个最值，寻找过程没有找到比它小的，就会一直找下去，会造成数组越界

int QSplit(int ary[], int left, int right)
{int keyi = left;while (left < right){//右边找大while (left < right && ary[right] >= ary[keyi]){right--;}//左边找小while (left < right && ary[left] <= ary[keyi]){left++;}Swap(&ary[left], ary[right]);}Swap(&ary[left], &ary[keyi]);return left;
}

针对上面两个问题修改，同时返回最后的keyi值

为什么left从0处开始找，如果从1处找，遇到下面的极端场景，会出现错误
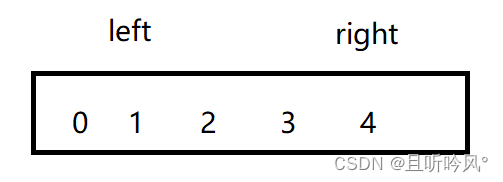
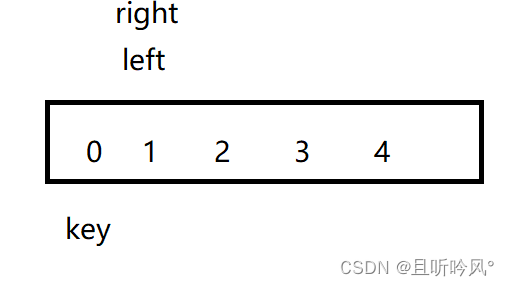
在这里插入图片描述

在这里插入图片描述
这样，到最后交换的时候key值就会换到1去，顺序就会变反。从0下标开始找，0和自己交换不会产生错误

保证相遇位置正确
如果left和right相遇的位置比keyi处值大,交换后也会出错误

1.左边做key,右边先走,保障了相遇位置比key小
2.右边做k,左边先走,保证了相遇位置比key大

以1的方法举例,R先走,就是R遇到L,有两种情况，第一种，L有比key大的值，这时R遇到L肯定是比key大的值交换。第二种，L没移动，R一直往左走遇到了L，相遇位置就是key的位置。这时，就是自己和自己交换

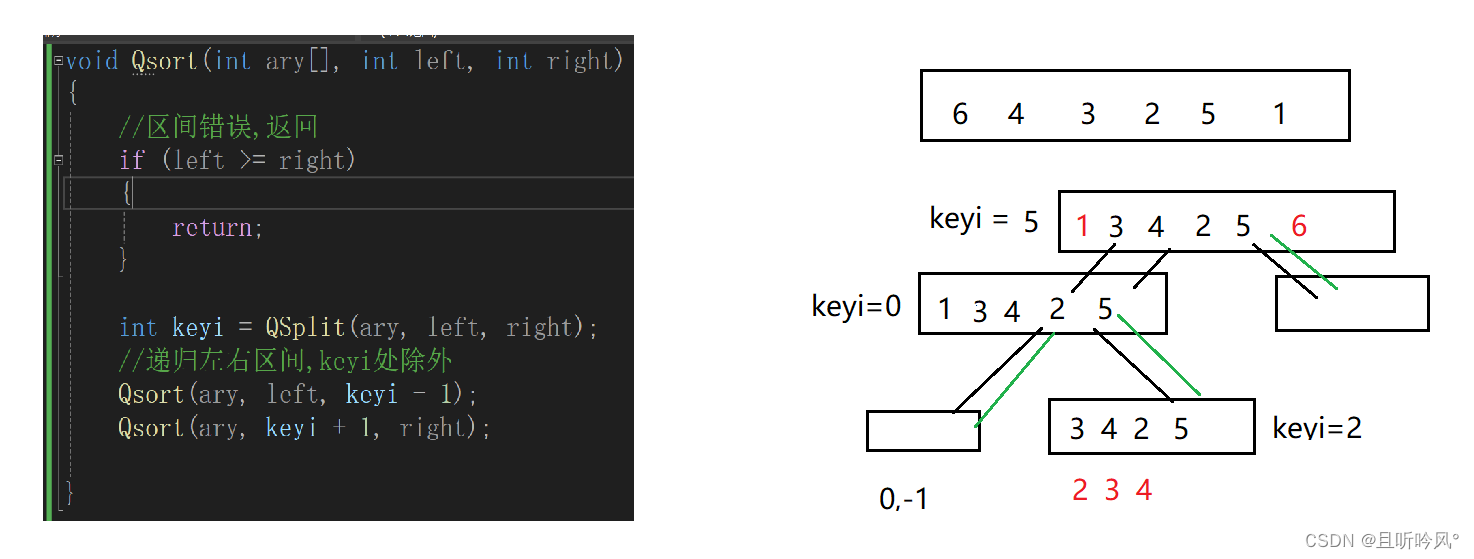
在这里插入图片描述

2.1.2 挖坑版

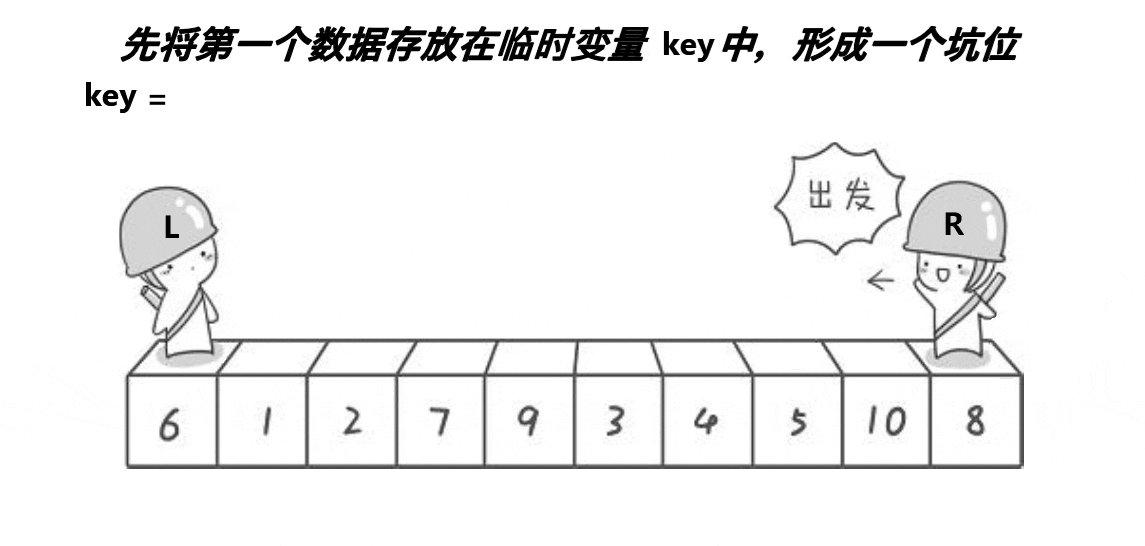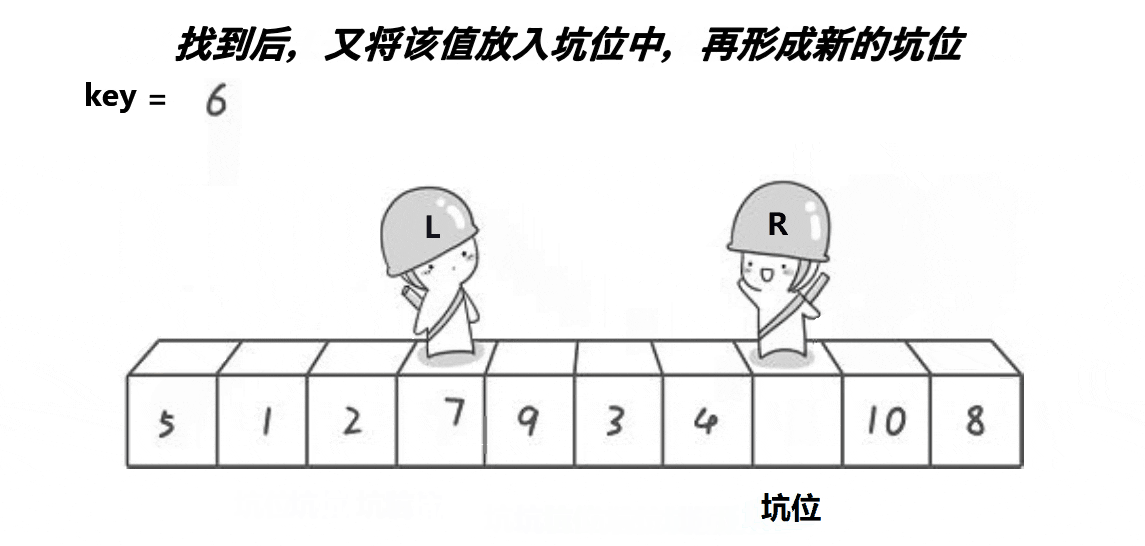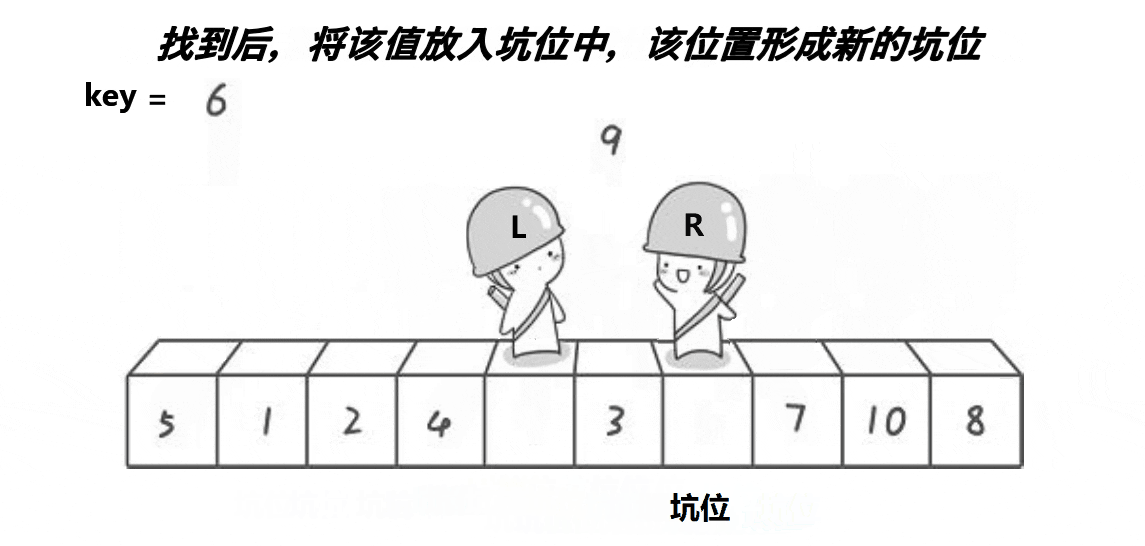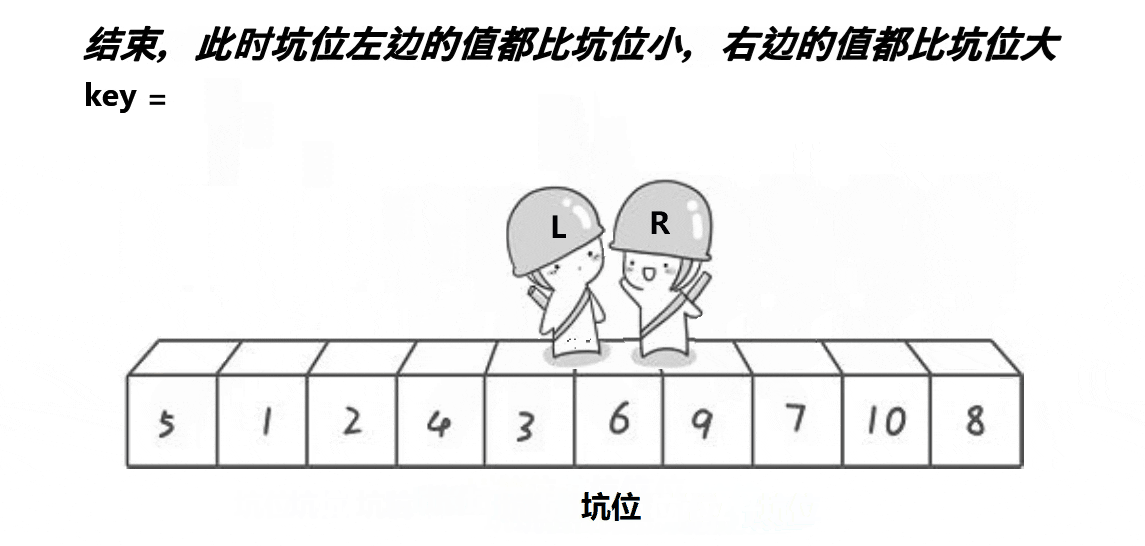
在这里插入图片描述

key为初始设定的坑位的值，R先走，遇到比key小的数将该数填到坑的位置，设定当前位置为坑。然后L走，找到大的数填为新坑，这样下去直到两个相遇，将key值填过来

挖坑法和hoare的几轮的结果可能不一样

int QSplit2(int ary[], int left, int right)
{
//key值和坑位int key = ary[left];int hole = left;while (left < right){//右边找小while (left < right && ary[right] >= key){right--;}ary[hole] = ary[right];hole = right;//左边找大while (left < right && ary[left] <= key){left++;}ary[hole] = ary[left];hole = left;}ary[hole] = key;return hole;
}

2.1.3 前后下标版

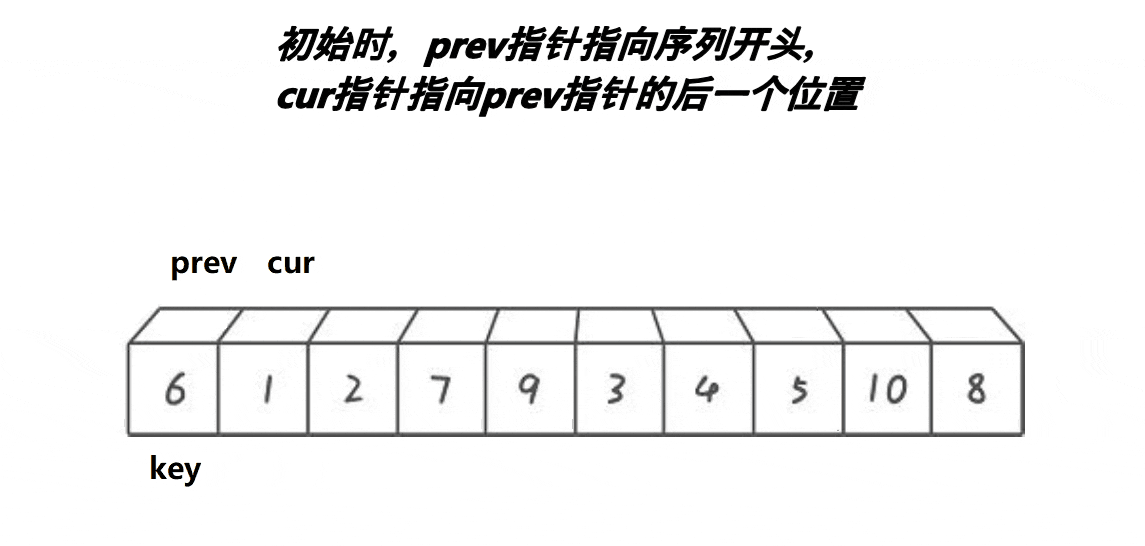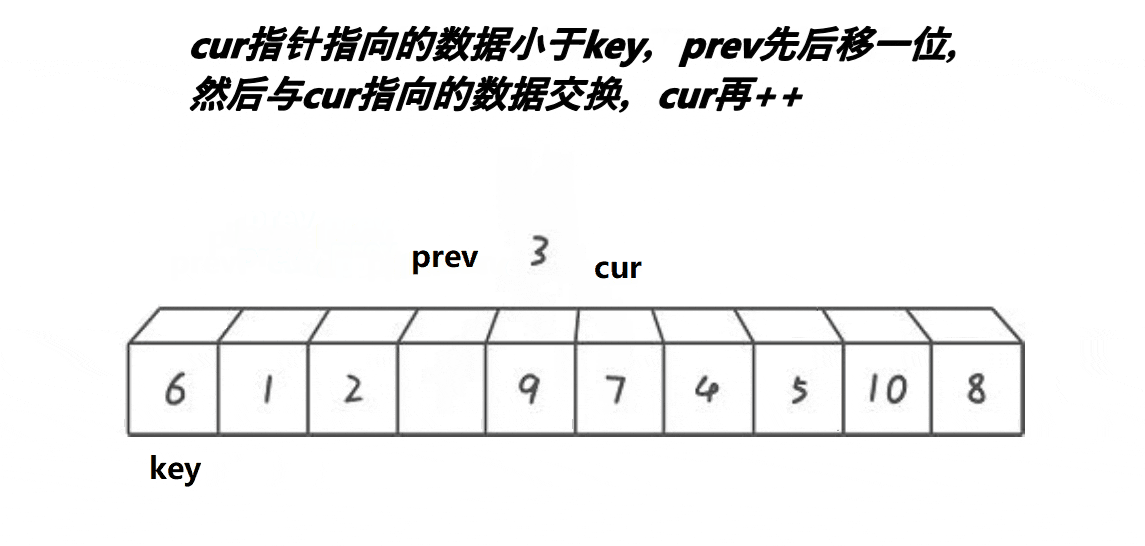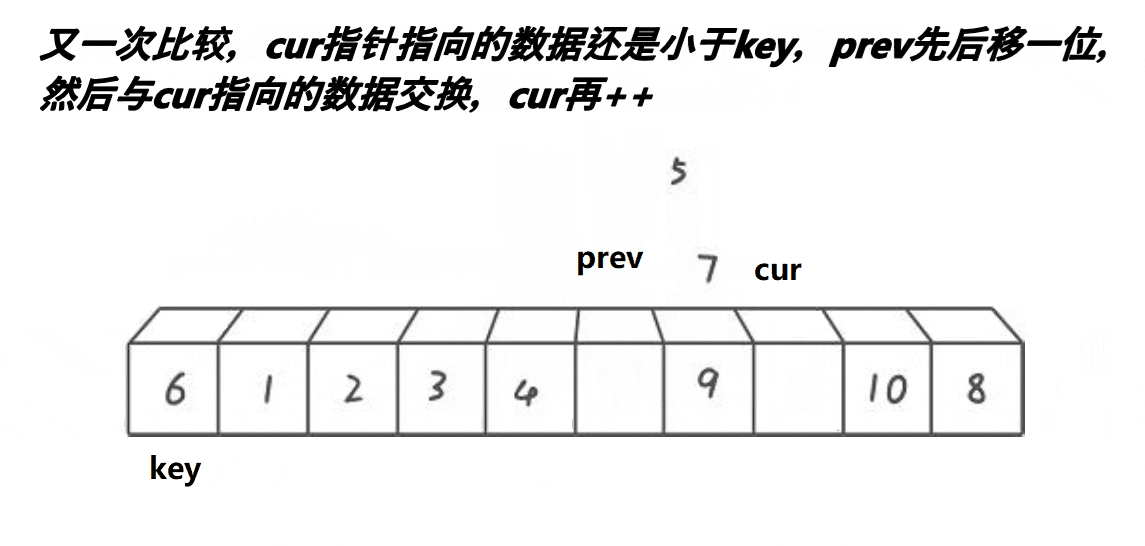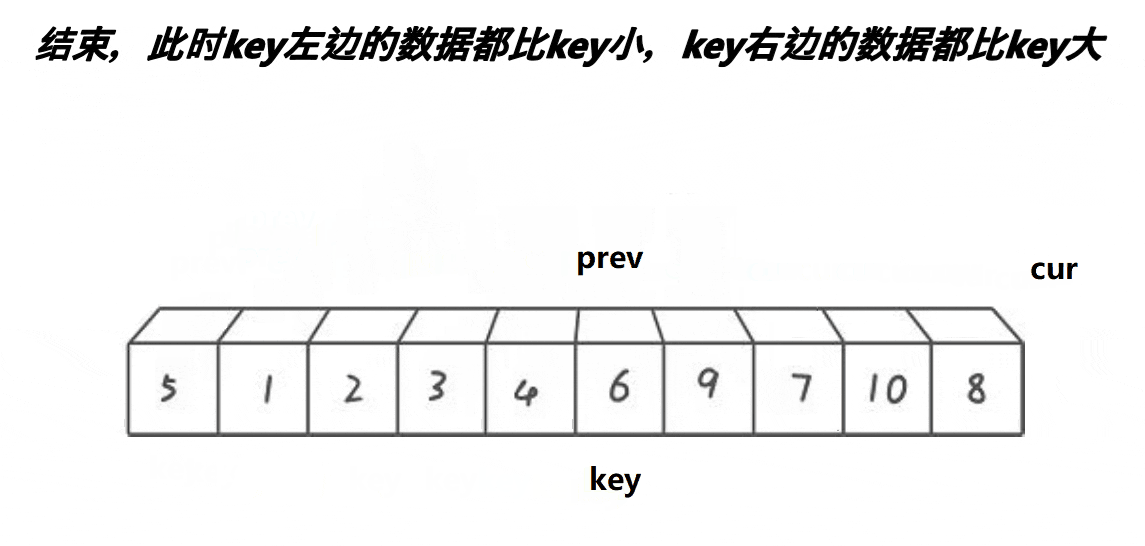
在这里插入图片描述

cur不断向后走,当cur处的值小于key处值时，pre先++，pre和cur的值交换，如果是自身就不用交换。直到cur超出数组，将pre处的值和key值交换。这种方法当cur和pre拉开差距后，中间间隔的值都是比key值大的，可以快速将这些值滚到最后

//前后下标
int QSplit3(int ary[], int left, int right)
{int pre = left;int cur = left + 1;int keyi = left;while (cur <= right){//cur值小于keyi时,且不等于自己if (ary[cur] < ary[keyi] && ++pre != cur){Swap(&ary[pre], &ary[cur]);}cur++;}Swap(&ary[pre], &ary[keyi]);keyi = pre;return keyi;
}

2.1.4 循环

替换递归过程，可以用栈，利用栈的先进后出，将左右区间先压进去。每次走一遍单趟可以吧新的区间按顺序压进去，处理不断处理栈顶的区间，区间不存在就返回。就可以模拟递归过程

下面是左边区间的栈过程
在这里插入图片描述

void CirculQsort(int ary[], int left, int right)
{Stk st;Init(&st);//压入左右下标Push(&st, left);Push(&st, right);while (!Empty(&st)){//取的时候相反int right = Top(&st);Pop(&st);int left = Top(&st);Pop(&st);int keyi = QSplit(ary, left, right);//区间存在压入if (keyi + 1 < right){Push(&st, keyi + 1);Push(&st, right);}if (left < keyi - 1){Push(&st, left);Push(&st, keyi - 1);}}Destory(&st);
}

2.2 特性

1.综合性能和使用场景都是比较好的，所以才叫快速排序
2.时间复杂度：最好,O(N*logN),取决于key的取值,如果key取值刚好是中位数,每次可以将数据正好分为两半。最差O(N²),有序的数列选出的key值
3.空间复杂度: O(logN)
4.稳定性: 不稳定

2.3 优化

2.3.1 key值优化

对于有序的数据快速排序的效率是很低的，因为key值每次取的是最值，划分出的区间作用很小，每次只能排一个数。所以对key值的取法优化可以解决有序数据的排序

三数取中

mid取left和right的中间位置，取三个下标的中间值

//三数取中
int GetIndex(int ary[], int left, int right)
{int mid = (left + right) / 2;if (ary[mid] > ary[left]){if (ary[mid] < ary[right]){return mid;}else if (ary[left] > ary[right]){return left;}else{return right;}}//ary[mid] < ary[left]else{if (ary[mid] > ary[right]){return mid;}else if (ary[left] > ary[right]){return right;}else{return left;}}
}int QSplit(int ary[], int left, int right)
{//三数取中int mid = GetIndex(ary, left, right);Swap(&ary[left], &ary[mid]);int keyi = left;while (left < right){//右边找小while (left < right && ary[right] >= ary[keyi]){right--;}//左边找大while (left < right && ary[left] <= ary[keyi]){left++;}Swap(&ary[left], &ary[right]);}Swap(&ary[left], &ary[keyi]);return left;
}