难度参考
难度:中等
分类:二叉树
难度与分类由我所参与的培训课程提供,但需要注意的是,难度与分类仅供参考。且所在课程未提供测试平台,故实现代码主要为自行测试的那种,以下内容均为个人笔记,旨在督促自己认真学习。
题目
给定一个二叉搜索树的根节点root和一个值ky,删除二叉搜索树中的key对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
示例1:
输入:root=[5,3,6,2,4,null,7],key=3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是3,所以我们首先找到3这个节点,然后删除它。
一个正确的答案是[5,4,6,2,null,nul,7]
示例2:
输入:root=[5,3,6,2,4,null,7],key=0
输出:[5,3,6,2,4,nu,7]
解释:二叉树不包含值为0的节点
思路
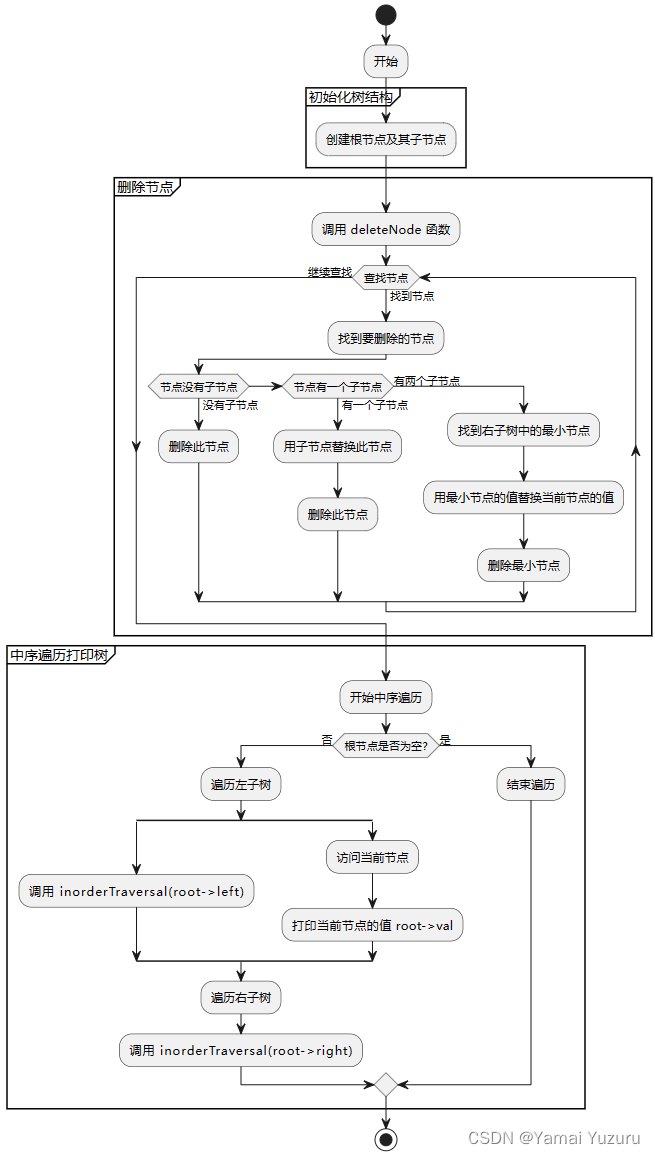
为了执行删除操作,我们需要遵循以下步骤:
- 首先找到需要删除的节点,即其值等于
key的节点。 - 如果节点未找到,即不存在值为
key的节点,则不需要删除操作,直接返回根节点。 - 如果节点找到了,则有几种情况:
- 节点是叶子节点(没有孩子节点):直接删除它,返回
nullptr。 - 节点有一个孩子节点:删除节点,并用其孩子节点代替自己。
- 节点有两个孩子节点:找到右子树中的最小值节点(或左子树中的最大值节点),替换当前节点的值,然后在相应的子树中删除该最小值节点(或最大值节点)。
- 节点是叶子节点(没有孩子节点):直接删除它,返回
示例
假设有以下的二叉搜索树:
5/ \3 6/ \ \2 4 7
我们想要删除值为 3 的节点。因此:
-
初始化和调用函数: 主程序创建了上述的二叉搜索树,并且呼叫了
deleteNode()函数,命令它删除值为 3 的节点。 -
开始查找要删除的节点:
deleteNode()函数开始在树中递归搜索值为 3 的节点。- 因为 3 小于根节点的值 5,它移动到根节点的左子节点,并且继续在该子树中查找。
-
找到要删除的节点: 节点 3 被找到了,由于它有两个子节点,我们必须采取特殊步骤去删除它。
- 先找到需要替代当前节点的节点。这个节点是当前节点右子树中的最小值节点,或者是当前节点左子树中的最大值节点。在我们的例子中,这个替代节点是值为 4 的节点,因为它是值为 3 的节点右子树中的最小值。
-
替代和删除:
- 我们将值为 4 的节点值放到值为 3 的节点。
5/ \4 6/ \ \2 4 7 - 然后,我们删除原本值为 4 的节点位置。
5/ \4 6/ \2 7 - 在这个特定情况下,由于值为 4 的节点没有子节点,它可以直接被移除。
- 我们将值为 4 的节点值放到值为 3 的节点。
-
调整树结构:
- 我们移除了值为 4 的节点,这造成值为 3 的原节点现在变成了值为 4。所以现在树的结构是这样的:
5/ \4 6/ \2 7
- 我们移除了值为 4 的节点,这造成值为 3 的原节点现在变成了值为 4。所以现在树的结构是这样的:
-
进行确认: 主程序中,我们再次通过中序遍历来确认树的结构。
- 中序遍历是这样的:2, 4, 5, 6, 7。可以确认值为 3 的节点已经被删除,并且二叉搜索树的属性仍然得到保持。
-
程序结束: 树已更新,程序也随之结束。
梳理
删除二叉搜索树(BST)中的节点需要考虑保持BST的特性,即对于任何节点,其左子树中的所有节点都比它小,右子树中的所有节点都比它大。对于删除操作,通常有三种情况需要处理:
-
删除没有子节点的节点:这是最简单的情况,可以直接将该节点移除,然后将其父节点对应的指针置为 null。
-
删除有一个子节点的节点:在这种情况下,需要删除节点,并将其子节点连接到该节点的父节点上。这样可以保证BST的特性不被破坏。
-
删除有两个子节点的节点:这是最复杂的情况,需要更多步骤来确保树的完整性。我们通常采用以下方法:
- 用继承者替换要删除的节点:继承者可以是要删除节点的右子树中的最小值节点(称为后继),或左子树中的最大值节点(称为前驱)。以后继为例,它是右子树上最接近我们要删除节点的那个值,但又比它大的最小节点。
- 删除继承者节点:由于找到的继承者是右子树中最小的节点,它不会有左子节点(如果有左子节点,那么这个左子节点将会比它更小,这与“是最小值”矛盾)。因此,我们可以轻易地将继承者节点提升为替换原节点位置的新节点,并处理好它的右子节点链接(如果有的话)。
删除过程中替换继承者的原因是我们希望删除操作之后BST的特性依然被保留。后继是右子树中最小的节点,它满足在左子树中的任何节点的值都比它小,在右子树中的任何节点的值都比它大的条件。当我们用后继替换掉要删除的节点后,就可以保证整个树仍然保持BST的所有特性,进行中序遍历时节点的值仍然是有序的。
这样操作能确保二叉搜索树在删除节点后仍然是有效的,即保持了二叉搜索树中序遍历结果为有序序列的特点。
代码
#include <iostream> // 包含输入输出流库
using namespace std; // 使用标准命名空间// 定义二叉树节点结构
struct TreeNode {int val; // 节点值TreeNode *left; // 左子节点指针TreeNode *right; // 右子节点指针// 初始化构造函数TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 删除节点函数定义
TreeNode* deleteNode(TreeNode* root, int key) {if (!root) return root; // 如果节点为空,则直接返回if (key < root->val) { // 如果要删除的值小于根节点的值,则在左子树中删除root->left = deleteNode(root->left, key);} else if (key > root->val) { // 如果要删除的值大于根节点的值,则在右子树中删除root->right = deleteNode(root->right, key);} else { // 找到要删除的节点// 如果节点同时拥有左右子节点if (root->left && root->right) {TreeNode* temp = root->right;while (temp->left) temp = temp->left; // 找到右子树中最小的节点root->val = temp->val; // 将该节点的值赋给根节点root->right = deleteNode(root->right, temp->val); // 删除右子树中的最小节点} else { // 节点最多只有一个子节点TreeNode* temp = root->left ? root->left : root->right; // 获得非空的子节点(如果有的话)delete root; // 删除当前节点root = temp; // 用非空的子节点替换当前节点}}return root; // 返回修改后的树的根节点
}// 中序遍历辅助函数定义
void inorderTraversal(TreeNode* root) {if (root) { // 如果节点非空inorderTraversal(root->left); // 遍历左子树cout << root->val << " "; // 访问当前节点,打印节点值inorderTraversal(root->right); // 遍历右子树}
}// 主函数
int main() {// 创建并初始化一个 BSTTreeNode* root = new TreeNode(5); // 根节点值为 5root->left = new TreeNode(3); // 根节点左子节点的值为 3root->right = new TreeNode(6); // 根节点右子节点的值为 6root->left->left = new TreeNode(2); // 左子节点的左子节点的值为 2root->left->right = new TreeNode(4); // 左子节点的右子节点的值为 4root->right->right = new TreeNode(7); // 右子节点的右子节点的值为 7// 打印初始 BSTcout << "Initial BST (inorder traversal): ";inorderTraversal(root); // 以中序遍历方式打印cout << endl;int key = 3; // 要删除的节点值root = deleteNode(root, key); // 调用删除函数// 打印删除特定节点后的 BSTcout << "BST after deleting node with key " << key << " (inorder traversal): ";inorderTraversal(root); // 以中序遍历方式打印cout << endl;return 0; // 主函数正确结束返回 0
}打卡


![洛谷C++简单题小练习day9—[AHOI2017]寻找探监点](https://img-blog.csdnimg.cn/direct/9e48c2a831ed4b75b553eab4cec4720a.jpeg)