为什么要示例演绎?
既然有了官方指南,咱们在官方指南上看看就可以了,为什么还要写示例演绎的文章呢?
其实对于初步了解TensorFlow的小伙伴们而言,示例演绎才是最重要的。
官方文档已经假定了您已经具备了相当合适的基础知识以及工作/学习环境,而这两点恰恰是很多小伙伴们的差异所在。

作者政安晨的工作生涯涉猎很广泛:从半导体芯片设计到硬件与射频通信电路开发,再从汇编语言的片上系统开发,C语言的Linux系统及其它嵌入式系统开发,中间件和应用开发,以及基于Python的数据抓取及分析业务开发(Python Web开发),还有go和nodejs的云平台产品开发,也包括图形编程、Arduino、智能硬件、传感器物联网、游戏产品、智能算法等等。
(有小伙伴可能会问了:你怎么可以做这么多东西,能精通得了吗?其实这里面有些根本逻辑是一直不会变的,每个人都有自己的内核,就像系统一样,内核要逐步加强而不能散乱,这样在职业技能的应用上才能千姿百态,向着一法通乃至万法通的状态探索。希望小伙伴们都能找到自己的内核。这个以后有机会给大家分享。)
顺着上面说,由此,老晨对官方文档的演绎不会只停留在单一维度上,在帮助大家踩坑的同时,也让大家看到直观地执行,希望这些文章成为大家的蹋脚石,让小伙伴们踩着我的理解继续前进!呵呵。
好,咱们开始!
Eager Execution
TensorFlow 的 Eager Execution 是一种命令式编程环境,可立即评估运算,无需构建计算图:运算会返回具体的值,而非构建供稍后运行的计算图。这样能使您轻松入门 TensorFlow 并调试模型,同时也减少了样板代码。要跟随本指南进行学习,请在交互式 python 解释器中运行以下代码示例。
Eager Execution 是用于研究和实验的灵活机器学习平台,具备以下特性:
- 直观的界面 - 自然地组织代码结构并使用 Python 数据结构。快速迭代小模型和小数据。
- 更方便的调试功能 - 直接调用运算以检查正在运行的模型并测试更改。使用标准 Python 调试工具立即报告错误。
- 自然的控制流 - 使用 Python 而非计算图控制流,简化了动态模型的规范。
Eager Execution 支持大部分 TensorFlow 运算和 GPU 加速。
官方有个注释:
{注:启用 Eager Execution 后可能会增加某些模型的开销。我们正在持续改进其性能,如果您遇到问题,请提交错误报告并分享您的基准。}
老晨:
与传统的TensorFlow方式不同,Eager Execution不需要显式地创建图,而是将操作应用于具体的张量数据并立即返回结果。
Eager Execution的工作原理如下:
- 张量表示:使用Eager Execution时,张量数据以普通的多维数组(numpy数组)的形式表示。
- 自动微分:Eager Execution支持自动计算梯度,使得在模型训练过程中能够方便地进行梯度下降等优化操作。
- 操作执行:在Eager Execution模式下,操作会立即执行并返回结果。这样可以方便地进行调试和验证。
- 动态模型构建:通过使用Python控制流语句,可以动态地构建模型,灵活地定义各种复杂的模型结构。
Eager Execution的主要优势是实时性和简洁性。它减少了构建静态计算图的复杂性,使得模型开发和调试过程更加直观和高效。在研究和探索新的模型架构时,Eager Execution可以帮助快速迭代和实验,而不需要考虑图构建的复杂性。同时,Eager Execution与TensorFlow的其他功能(如TensorBoard可视化和分布式训练)也可以无缝集成使用。
设置和基本用法
在这篇演绎中,我是基于本地环境运行TensorFLow的(CPU版本),对于这样指南性质的示例来说,足够了。
我照例打开了Jupyter Notebook,并加载了TensorFlow的虚拟环境,不清楚的小伙伴看我机器学习笔记里的文章:
政安晨的机器学习笔记——跟着演练快速理解TensorFlow(适合新手入门)![]() https://blog.csdn.net/snowdenkeke/article/details/135950931
https://blog.csdn.net/snowdenkeke/article/details/135950931
import osimport tensorflow as tfimport cProfile在 Tensorflow 2.0 中,默认启用 Eager Execution。
tf.executing_eagerly()老晨执行:

现在您可以运行 TensorFlow 运算,结果将立即返回:
x = [[2.]]
m = tf.matmul(x, x)
print("hello, {}".format(m))老晨执行:

启用 Eager Execution 会改变 TensorFlow 运算的行为方式 - 现在它们会立即评估并将值返回给 Python。tf.Tensor 对象会引用具体值,而非指向计算图中节点的符号句柄。由于无需构建计算图并稍后在会话中运行,可以轻松使用 print() 或调试程序检查结果。评估、输出和检查张量值不会中断计算梯度的流程。
Eager Execution 可以很好地配合 NumPy 使用。NumPy 运算接受 tf.Tensor 参数。TensorFlow tf.math 运算会将 Python 对象和 NumPy 数组转换为 tf.Tensor 对象。tf.Tensor.numpy 方法会以 NumPy ndarray 的形式返回该对象的值。
a = tf.constant([[1, 2],[3, 4]])
print(a)老晨执行:

老晨:
这个例子定义了一个二阶张量(也称二维张量),它的形状是(2, 2),类型是32位整型。
咱们人类的大脑其实更容易理解具象的东西,婴幼儿时期主要是具象思维,后来慢慢长大,逐步有了抽象思维(逻辑、推理等等)能力。所以在机器学习的领域中,您看到的很多现象的背后隐含方式都是要把抽象的东西转换成具象的表达,比如我们这里说的张量和形状。其实这没有什么好神秘的,大家不要被各种技术词儿给吓到了,技术词儿也是一些人说出来给另一些人听的(也包括我,呵呵)。
官方指南中接下来就是用张量做个运算。
# Broadcasting support
b = tf.add(a, 1)
print(b)老晨执行:

老晨:
小伙伴们仔细观察,张量b是在a张量的基础上各元素加1得来的。
# Operator overloading is supported
print(a * b)老晨执行:

老晨:
张量的乘法小伙伴们学过离散数学的就会清楚一点,这个就是矩阵乘法,因为a和b都是二阶张量,所以,张量a乘以张量b,就是张量a中对应位置与张量b中对应位置相乘,得出的新张量就是您看到的[[2 6] [12 20]],形状当然还是(2,2)。
接下来,官方指南中又演示了一些运算例子(基于NumPy库):
# Use NumPy values
import numpy as npc = np.multiply(a, b)
print(c)# Obtain numpy value from a tensor:
print(a.numpy())
# => [[1 2]
# [3 4]]老晨执行:

动态控制流
Eager Execution 的一个主要优势是,在执行模型时,主机语言的所有功能均可用。因此,编写下面这类(FIZZBUZZ)的代码会很容易:
def fizzbuzz(max_num):counter = tf.constant(0)max_num = tf.convert_to_tensor(max_num)for num in range(1, max_num.numpy()+1):num = tf.constant(num)if int(num % 3) == 0 and int(num % 5) == 0:print('FizzBuzz')elif int(num % 3) == 0:print('Fizz')elif int(num % 5) == 0:print('Buzz')else:print(num.numpy())counter += 1fizzbuzz(15)老晨执行(定义函数,传参执行):

这段代码具有依赖于张量值的条件语句并会在运行时输出这些值。
Eager 训练
计算梯度
自动微分在对实现机器学习算法(例如用于训练神经网络的反向传播)十分有用。在 Eager Execution 期间,请使用 tf.GradientTape 跟踪运算以便稍后计算梯度。
您可以在 Eager Execution 中使用 tf.GradientTape 来训练和/或计算梯度。这对复杂的训练循环特别有用。
由于在每次调用期间都可能进行不同运算,所有前向传递的运算都会记录到“条带”中。要计算梯度,请反向播放条带,然后丢弃。特定 tf.GradientTape 只能计算一个梯度;后续调用会引发运行时错误。
政安晨:先了解两个术语
自动微分(Automatic Differentiation)是一种计算导数的方法,它在机器学习中起着重要的作用。在机器学习中,我们经常需要计算模型参数对于损失函数的梯度,以便使用梯度下降等优化算法来更新参数。
传统的数值微分方法往往需要使用数值近似的方式来计算导数,这样会引入舍入误差,并且计算效率较低。自动微分通过利用计算图的方式,可以有效地计算出精确的导数值,而且计算效率较高。
具体而言,自动微分通过将复杂的计算过程拆解为一系列基本的运算操作,然后利用链式法则计算相应的导数,从而得到每个操作的导数值。这种方式可以避免传统数值微分方法中存在的误差累积问题,并且可以高效地计算出所有参数的导数。
在机器学习中,自动微分被广泛应用于各种模型的训练过程中,包括神经网络、支持向量机、决策树等。通过自动微分,我们可以方便地计算出模型参数对于损失函数的梯度,并根据梯度来更新参数,从而提高模型的性能和准确度。
总之,自动微分是机器学习中计算导数的一种高效而准确的方法,它在模型训练和参数优化中起着重要的作用。
反向传播(backpropagation)是一种机器学习中用于训练神经网络的算法。它通过计算损失函数对网络中每个参数的梯度来更新参数的值,从而使网络的输出接近于预期的目标。
具体来说,反向传播通过两个步骤来计算梯度。首先,它根据网络的输入和当前参数的值来计算网络的输出。然后,它根据损失函数来计算输出与目标值之间的差异,并将误差通过网络向后传播。在这个过程中,反向传播通过链式法则计算每个参数对于损失函数的梯度。最后,使用计算出的梯度来更新参数的值,以降低损失函数的值。
反向传播具有以下几个重要的特点和优势:
- 反向传播是一种自动化的方法,可以直接计算网络中每个参数对于整个网络的输出的影响,而不需要手动推导导数。
- 反向传播可以高效地计算网络中大量参数的梯度,使得神经网络的训练更加快速和高效。
- 反向传播可以用于训练深度神经网络,使得神经网络可以学习更复杂、更抽象的特征和模式。
总之,反向传播在机器学习中扮演着重要的角色,为神经网络的训练提供了一种高效而自动化的方法,使得神经网络可以学习和逼近复杂的函数关系。
w = tf.Variable([[1.0]])
with tf.GradientTape() as tape:loss = w * wgrad = tape.gradient(loss, w)
print(grad) # => tf.Tensor([[ 2.]], shape=(1, 1), dtype=float32)老晨执行:

训练模型
以下示例创建了一个多层模型,该模型会对标准 MNIST 手写数字进行分类(政安晨:我有篇文章专门讲这个手写数字的数据集,是美国80年代训练的,在机器学习领域里经常用)。
政安晨的机器学习笔记——基于Anaconda安装TensorFlow并尝试一个神经网络小实例![]() https://blog.csdn.net/snowdenkeke/article/details/135841281好,我们接着下面的示例说,该示例演示了在 Eager Execution 环境中构建可训练计算图的优化器和层 API。
https://blog.csdn.net/snowdenkeke/article/details/135841281好,我们接着下面的示例说,该示例演示了在 Eager Execution 环境中构建可训练计算图的优化器和层 API。
# Fetch and format the mnist data
(mnist_images, mnist_labels), _ = tf.keras.datasets.mnist.load_data()dataset = tf.data.Dataset.from_tensor_slices((tf.cast(mnist_images[...,tf.newaxis]/255, tf.float32),tf.cast(mnist_labels,tf.int64)))
dataset = dataset.shuffle(1000).batch(32)# Build the model
mnist_model = tf.keras.Sequential([tf.keras.layers.Conv2D(16,[3,3], activation='relu',input_shape=(None, None, 1)),tf.keras.layers.Conv2D(16,[3,3], activation='relu'),tf.keras.layers.GlobalAveragePooling2D(),tf.keras.layers.Dense(10)
])即使没有训练,也可以在 Eager Execution 中调用模型并检查输出:
for images,labels in dataset.take(1):print("Logits: ", mnist_model(images[0:1]).numpy())政安晨执行:

虽然 Keras 模型有内置训练循环(使用 fit 方法),但有时您需要进行更多自定义。下面是一个使用 Eager Execution 实现训练循环的示例:
optimizer = tf.keras.optimizers.Adam()
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True)loss_history = []注:请在 tf.debugging 中使用断言函数检查条件是否成立。这在 Eager Execution 和计算图执行中均有效。
def train_step(images, labels):with tf.GradientTape() as tape:logits = mnist_model(images, training=True)# Add asserts to check the shape of the output.tf.debugging.assert_equal(logits.shape, (32, 10))loss_value = loss_object(labels, logits)loss_history.append(loss_value.numpy().mean())grads = tape.gradient(loss_value, mnist_model.trainable_variables)optimizer.apply_gradients(zip(grads, mnist_model.trainable_variables))def train(epochs):for epoch in range(epochs):for (batch, (images, labels)) in enumerate(dataset):train_step(images, labels)print ('Epoch {} finished'.format(epoch))train(epochs = 3)政安晨:有时候您执行Jupyter单元格的时候,可能会遇到执行后没有反应,不要慌,重启内核!
应该是您执行某段代码的时候让内核异常而部分不响应。
其实,我在演绎到这里的时候,已经发现我的CPU版内核(TensorFlow)开始出现不稳定的情况,所以,我切换到在线Colab继续为大家演绎。
政安晨执行:

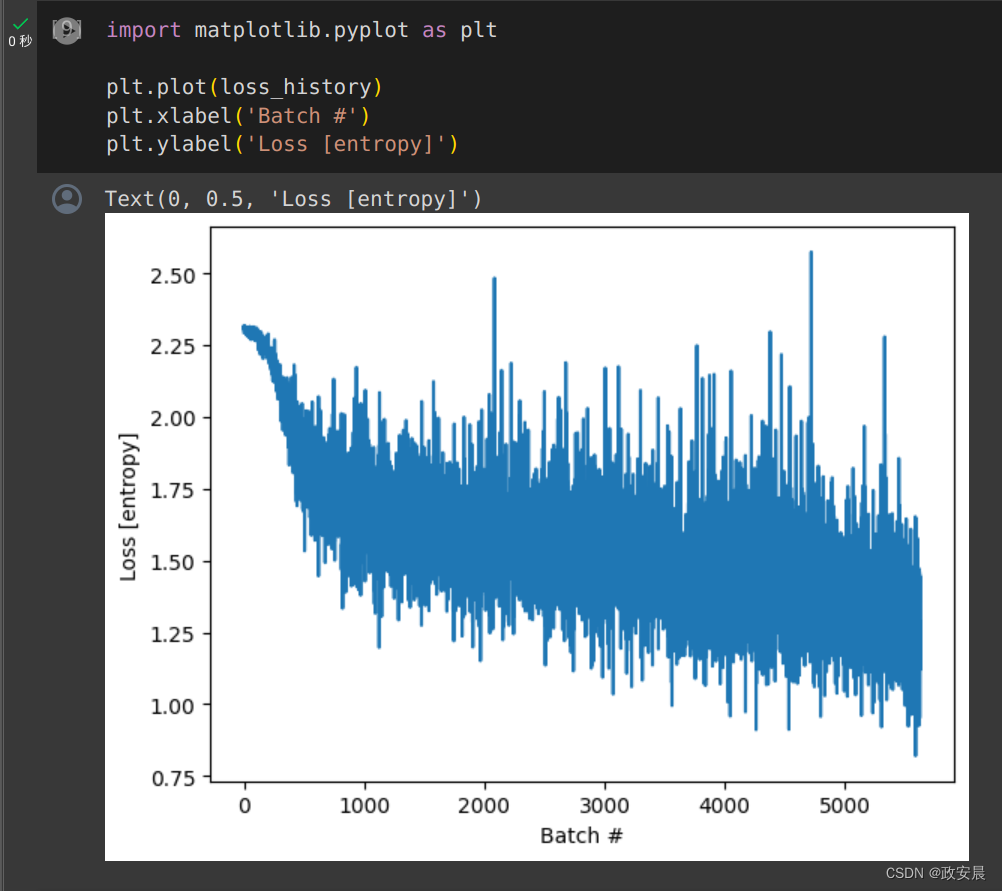
import matplotlib.pyplot as pltplt.plot(loss_history)
plt.xlabel('Batch #')
plt.ylabel('Loss [entropy]')图表显示:
变量和优化器
tf.Variable 对象会存储在训练期间访问的可变、类似于 tf.Tensor 的值,以更简单地实现自动微分。
变量的集合及其运算方法可以封装到层或模型中。有关详细信息,请参阅自定义 Keras 层和模型。层和模型之间的主要区别在于模型添加了如下方法:Model.fit、Model.evaluate 和 Model.save。
例如,上面的自动微分示例可以改写为:
class Linear(tf.keras.Model):def __init__(self):super(Linear, self).__init__()self.W = tf.Variable(5., name='weight')self.B = tf.Variable(10., name='bias')def call(self, inputs):return inputs * self.W + self.B# A toy dataset of points around 3 * x + 2
NUM_EXAMPLES = 2000
training_inputs = tf.random.normal([NUM_EXAMPLES])
noise = tf.random.normal([NUM_EXAMPLES])
training_outputs = training_inputs * 3 + 2 + noise# The loss function to be optimized
def loss(model, inputs, targets):error = model(inputs) - targetsreturn tf.reduce_mean(tf.square(error))def grad(model, inputs, targets):with tf.GradientTape() as tape:loss_value = loss(model, inputs, targets)return tape.gradient(loss_value, [model.W, model.B])下一步:
- 创建模型。
- 损失函数对模型参数的导数。
- 基于导数的变量更新策略。
model = Linear()
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)print("Initial loss: {:.3f}".format(loss(model, training_inputs, training_outputs)))steps = 300
for i in range(steps):grads = grad(model, training_inputs, training_outputs)optimizer.apply_gradients(zip(grads, [model.W, model.B]))if i % 20 == 0:print("Loss at step {:03d}: {:.3f}".format(i, loss(model, training_inputs, training_outputs)))政安晨执行:

print("Final loss: {:.3f}".format(loss(model, training_inputs, training_outputs)))print("W = {}, B = {}".format(model.W.numpy(), model.B.numpy()))政安晨执行:

注:变量将一直存在,直至删除对 Python 对象的最后一个引用,并删除该变量。
基于对象的保存
tf.keras.Model 包括一个方便的 save_weights 方法,您可以通过该方法轻松创建检查点:
model.save_weights('weights')
status = model.load_weights('weights')您可以使用 tf.train.Checkpoint 完全控制此过程。
x = tf.Variable(10.)
checkpoint = tf.train.Checkpoint(x=x)x.assign(2.) # Assign a new value to the variables and save.
checkpoint_path = './ckpt/'
checkpoint.save('./ckpt/')政安晨执行:

x.assign(11.) # Change the variable after saving.# Restore values from the checkpoint
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_path))print(x) # => 2.0政安晨执行:

要保存和加载模型,tf.train.Checkpoint 会存储对象的内部状态,而无需隐藏变量。要记录 model、optimizer 和全局步骤的状态,请将它们传递到 tf.train.Checkpoint:
model = tf.keras.Sequential([tf.keras.layers.Conv2D(16,[3,3], activation='relu'),tf.keras.layers.GlobalAveragePooling2D(),tf.keras.layers.Dense(10)
])
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
checkpoint_dir = 'path/to/model_dir'
if not os.path.exists(checkpoint_dir):os.makedirs(checkpoint_dir)
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
root = tf.train.Checkpoint(optimizer=optimizer,model=model)root.save(checkpoint_prefix)
root.restore(tf.train.latest_checkpoint(checkpoint_dir))政安晨执行:

注:在许多训练循环中,会在调用 tf.train.Checkpoint.restore 后创建变量。这些变量将在创建后立即恢复,并且可以使用断言来确保检查点已完全加载。
面向对象的指标
tf.keras.metrics 会被存储为对象。可以通过将新数据传递给可调用对象来更新指标,并使用 tf.keras.metrics.result 方法检索结果,例如:
m = tf.keras.metrics.Mean("loss")
m(0)
m(5)
m.result() # => 2.5
m([8, 9])
m.result() # => 5.5政安晨执行:

摘要和 TensorBoard
TensorBoard 是一种可视化工具,用于了解、调试和优化模型训练过程。它使用在执行程序时编写的摘要事件。
您可以在 Eager Execution 中使用 tf.summary 记录变量摘要。例如,要每 100 个训练步骤记录一次 loss 的摘要,请运行以下代码:
logdir = "./tb/"
writer = tf.summary.create_file_writer(logdir)steps = 1000
with writer.as_default(): # or call writer.set_as_default() before the loop.for i in range(steps):step = i + 1# Calculate loss with your real train function.loss = 1 - 0.001 * stepif step % 100 == 0:tf.summary.scalar('loss', loss, step=step)ls tb/政安晨执行:

自动微分高级主题
动态模型
tf.GradientTape 也可以用于动态模型。下面这个回溯线搜索算法示例看起来就像普通的 NumPy 代码,但它的控制流比较复杂,存在梯度且可微分:
def line_search_step(fn, init_x, rate=1.0):with tf.GradientTape() as tape:# Variables are automatically tracked.# But to calculate a gradient from a tensor, you must `watch` it.tape.watch(init_x)value = fn(init_x)grad = tape.gradient(value, init_x)grad_norm = tf.reduce_sum(grad * grad)init_value = valuewhile value > init_value - rate * grad_norm:x = init_x - rate * gradvalue = fn(x)rate /= 2.0return x, value自定义梯度
自定义梯度是重写梯度的一种简单方法。在前向函数中,定义相对于输入、输出或中间结果的梯度。例如,下面是在后向传递中裁剪梯度范数的一种简单方法:
@tf.custom_gradient
def clip_gradient_by_norm(x, norm):y = tf.identity(x)def grad_fn(dresult):return [tf.clip_by_norm(dresult, norm), None]return y, grad_fn自定义梯度通常用来为运算序列提供数值稳定的梯度:
def log1pexp(x):return tf.math.log(1 + tf.exp(x))def grad_log1pexp(x):with tf.GradientTape() as tape:tape.watch(x)value = log1pexp(x)return tape.gradient(value, x)# The gradient computation works fine at x = 0.
grad_log1pexp(tf.constant(0.)).numpy()政安晨执行:

# However, x = 100 fails because of numerical instability.
grad_log1pexp(tf.constant(100.)).numpy()政安晨执行:

在此例中,log1pexp 函数可以通过自定义梯度进行分析简化。下面的实现重用了在前向传递期间计算的 tf.exp(x) 值,通过消除冗余计算使其变得更加高效:
@tf.custom_gradient
def log1pexp(x):e = tf.exp(x)def grad(dy):return dy * (1 - 1 / (1 + e))return tf.math.log(1 + e), graddef grad_log1pexp(x):with tf.GradientTape() as tape:tape.watch(x)value = log1pexp(x)return tape.gradient(value, x)# As before, the gradient computation works fine at x = 0.
grad_log1pexp(tf.constant(0.)).numpy()# And the gradient computation also works at x = 100.
grad_log1pexp(tf.constant(100.)).numpy()政安晨执行:

性能
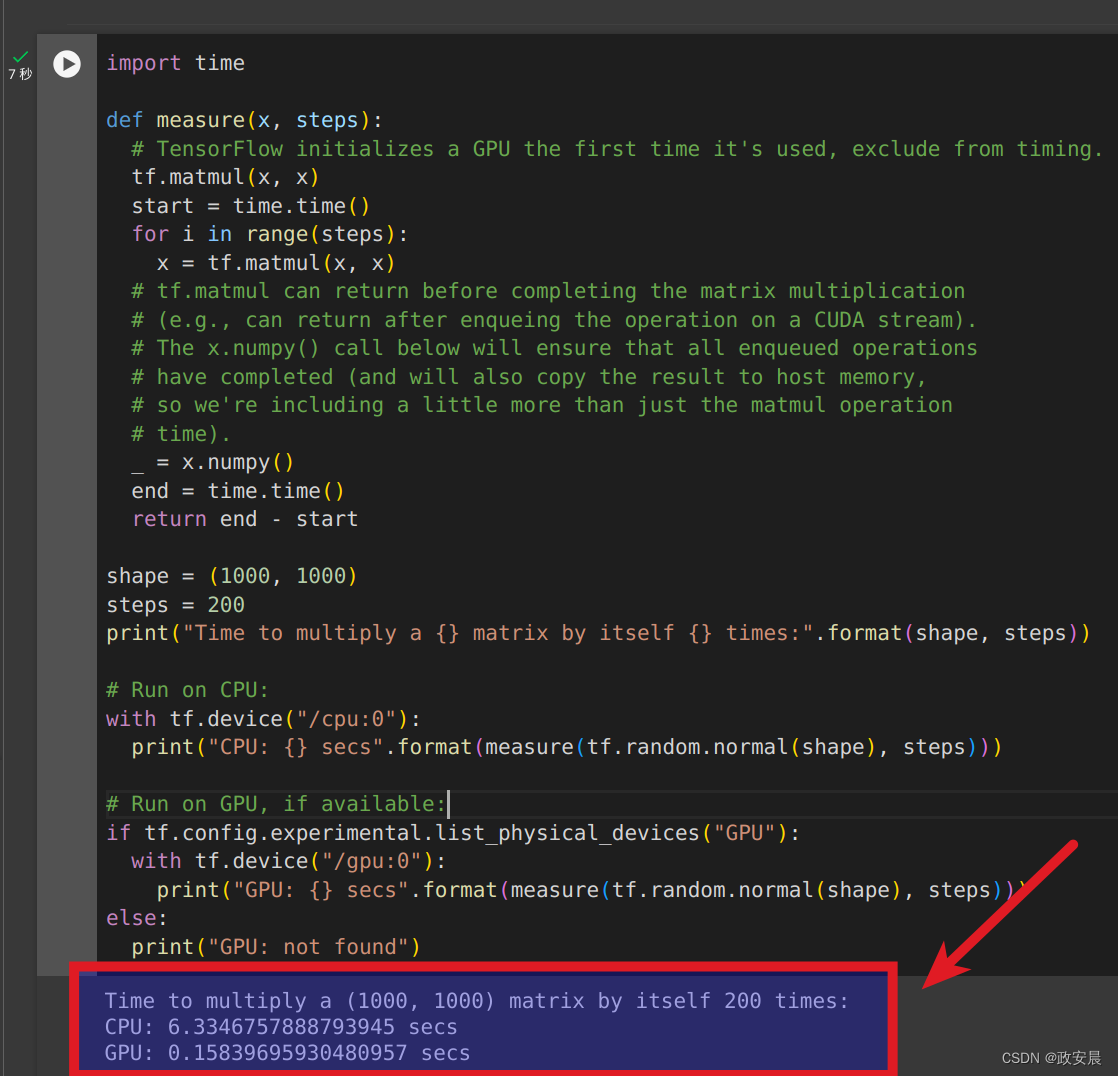
在 Eager Execution 期间,计算会自动分流到 GPU。如果想控制计算运行的位置,可将其放在 tf.device('/gpu:0') 块(或 CPU 等效块)中:
import timedef measure(x, steps):# TensorFlow initializes a GPU the first time it's used, exclude from timing.tf.matmul(x, x)start = time.time()for i in range(steps):x = tf.matmul(x, x)# tf.matmul can return before completing the matrix multiplication# (e.g., can return after enqueing the operation on a CUDA stream).# The x.numpy() call below will ensure that all enqueued operations# have completed (and will also copy the result to host memory,# so we're including a little more than just the matmul operation# time)._ = x.numpy()end = time.time()return end - startshape = (1000, 1000)
steps = 200
print("Time to multiply a {} matrix by itself {} times:".format(shape, steps))# Run on CPU:
with tf.device("/cpu:0"):print("CPU: {} secs".format(measure(tf.random.normal(shape), steps)))# Run on GPU, if available:
if tf.config.experimental.list_physical_devices("GPU"):with tf.device("/gpu:0"):print("GPU: {} secs".format(measure(tf.random.normal(shape), steps)))
else:print("GPU: not found")政安晨执行:
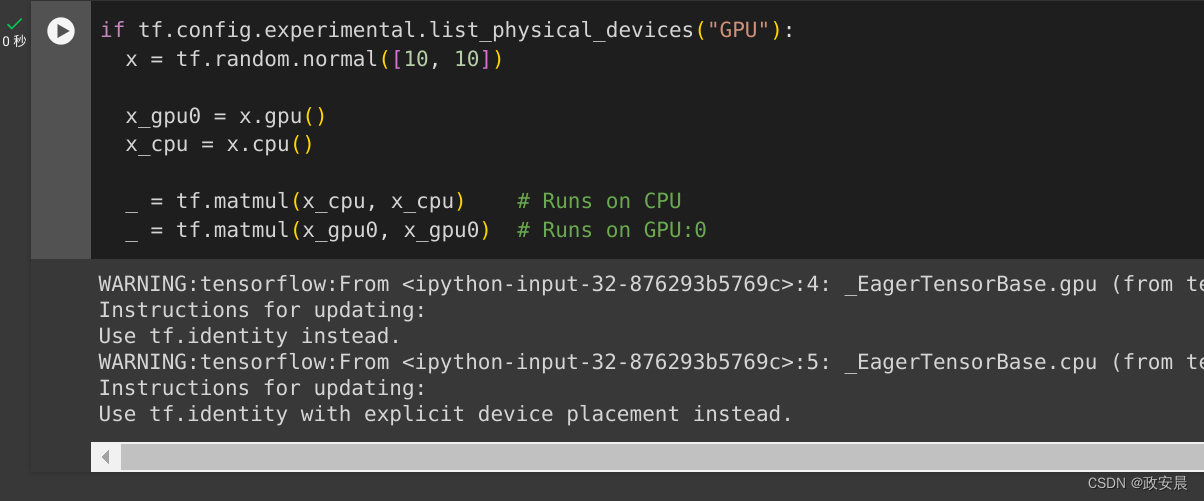
可以将 tf.Tensor 对象复制到不同设备来执行其运算:
if tf.config.experimental.list_physical_devices("GPU"):x = tf.random.normal([10, 10])x_gpu0 = x.gpu()x_cpu = x.cpu()_ = tf.matmul(x_cpu, x_cpu) # Runs on CPU_ = tf.matmul(x_gpu0, x_gpu0) # Runs on GPU:0政安晨执行:
基准
对于计算量繁重的模型(如在 GPU 上训练的 ResNet50),Eager Execution 性能与 tf.function 执行相当。但是对于计算量较小的模型来说,这种性能差距会越来越大,并且在为有大量小运算的模型优化热代码路径方面,其性能还有待提升。
使用函数
虽然 Eager Execution 增强了开发和调试的交互性,但 TensorFlow 1.x 样式的计算图执行在分布式训练、性能优化和生产部署方面具有优势。为了弥补这一差距,TensorFlow 2.0 通过 tf.function API 引入了 function。
写在最后
咱们匆匆忙忙完成了这篇指南的演绎,其实这里面很多知识点,这个篇幅已经很长了(12000余字),我就不在这里讲解了,这篇文章里就做为完整演绎的留档吧。(以供大家参考)