目录

递归遍历的三步骤：

DFS/回溯模板 

 练习

1.三角形路径和最大搜索

 （一）前序DFS（从上至下搜索，实际是暴力解法，测试超时）

（二）后序DFS（自底向上搜索，设置memory数组记录各节点子树的最大路径和，相同子树剪枝优化，AC）

（1）递归无返回值

（2）递归有返回值

---

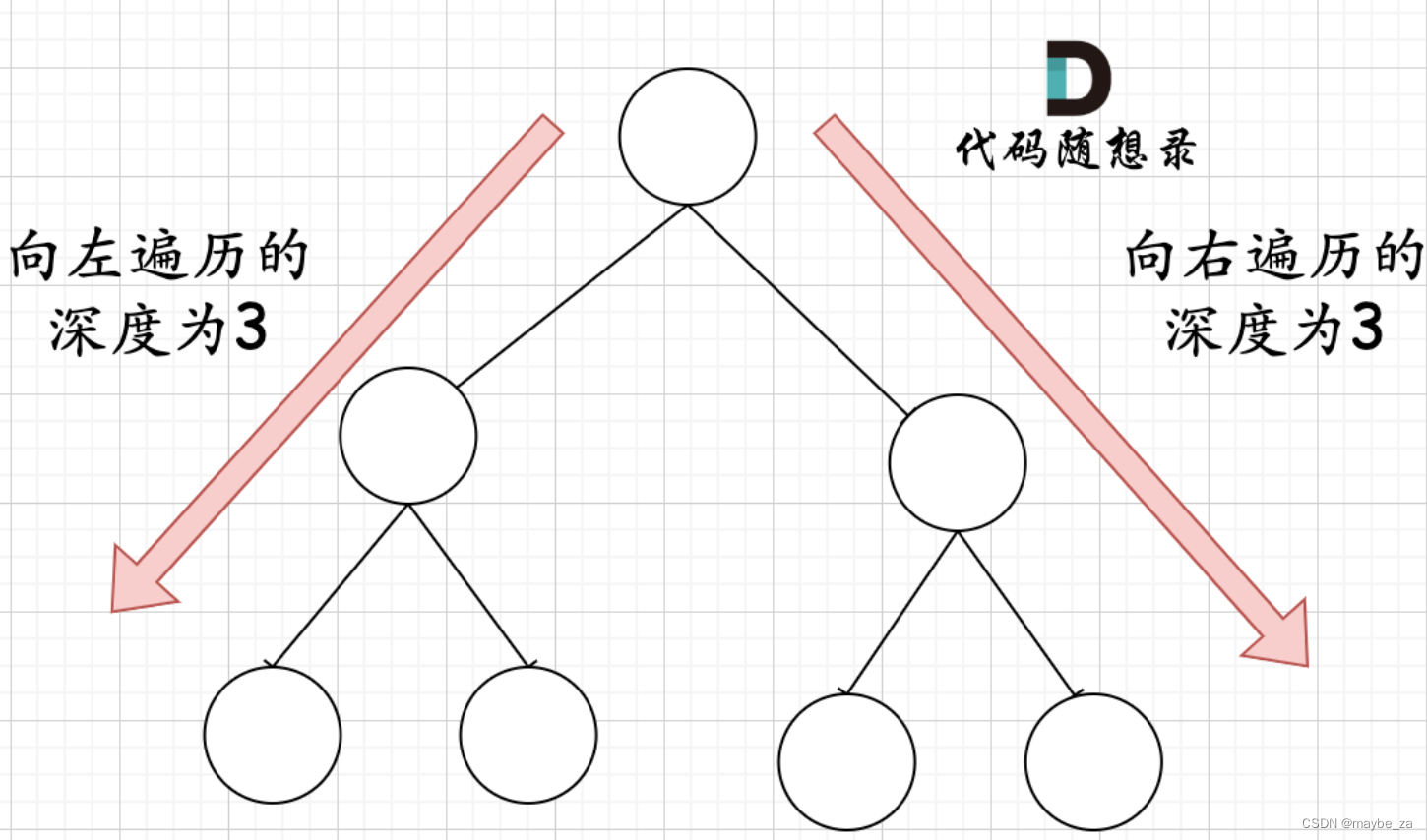
         DFS是一种遍历/搜索树和图的算法，感觉和回溯算法类似，思想都是沿着树的深度进行（按照前序/中序/后序）递归搜索，直至搜索到某一路径的叶节点（或满足某终止条件），后沿深度进行回溯，搜索其余路径。访问完所有可能路径后，返回目标任务最优解或所有满足条件的路径。

        这实际就是一种暴力解法，时间复杂度高，为了提高算法效率，可分析题目，结合记忆法等对树进行剪枝优化。

递归遍历的三步骤：

1.递归函数的参数、返回值（每层递归需要处理的数据）

2.递归终止条件（终止条件错误总会导致操纵系统的内存栈溢出错误）

3.单层递归逻辑（每层递归需要执行的操作）

DFS/回溯模板 

void dfs(参数) {if (终止条件) {存放结果;return;}for (选择：本节点所连接的其他节点) {处理节点;dfs(图，选择的节点); // 递归回溯，撤销处理结果}
}

 练习

1.三角形路径和最大搜索

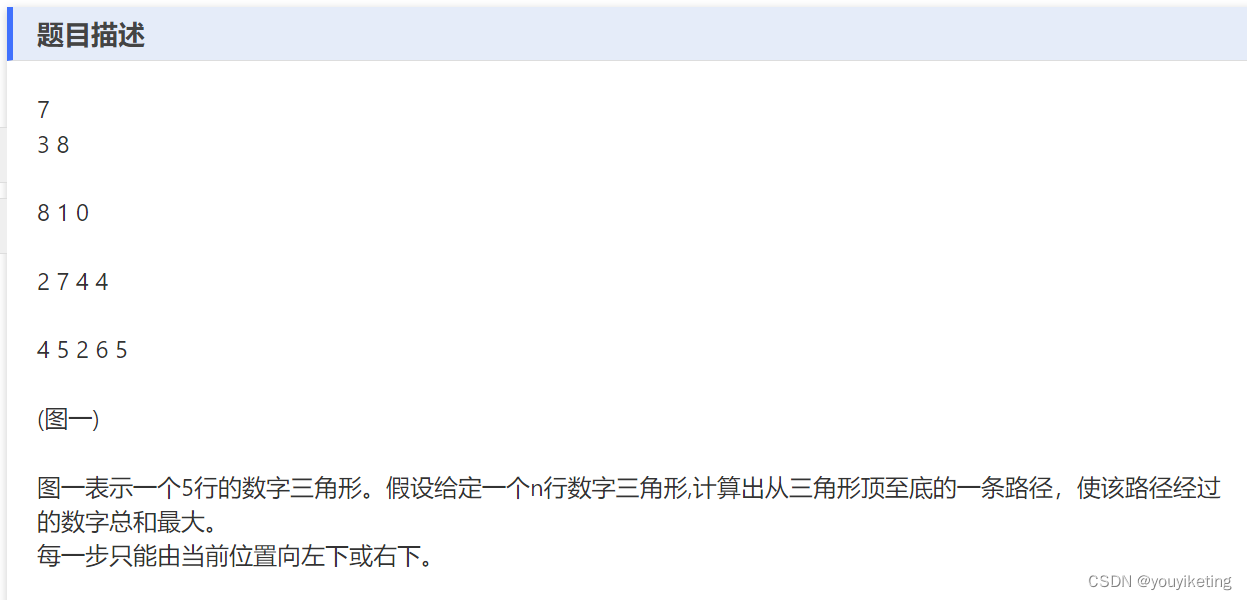
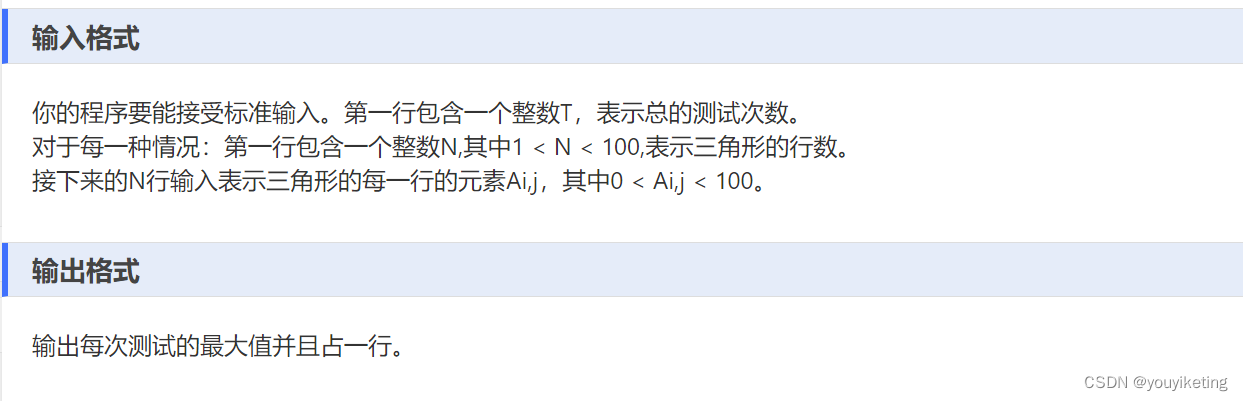
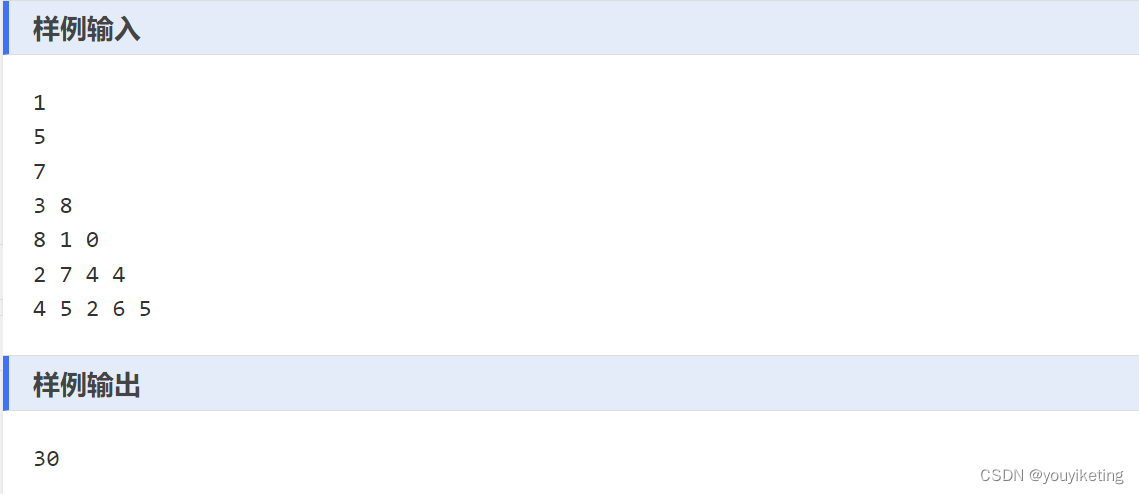
 （一）前序DFS（从上至下搜索，实际是暴力解法，测试超时）

#include<iostream>
#include<vector>
using namespace std;void output(vector<vector<int>>& input){for(int i=0; i<input.size(); i++){for(auto it=input[i].begin(); it!= input[i].end(); it++){cout<<*it<<" ";}cout<<endl;}
}struct TreeNode{int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};class solution
{
private:int maxSum;// 前序深度遍历void traversal(vector<vector<int>>& tree, int depth, int width, int sum){//if(depth >= tree.size()){if(sum > maxSum) maxSum = sum;return;}// midsum += tree[depth][width];// lefttraversal(tree, depth+1, width, sum);// righttraversal(tree, depth+1, width+1, sum);}
public:int getMaxPathSum(vector<vector<int>>& input_tree){maxSum = -1;traversal(input_tree, 0, 0, 0);return maxSum;}
};int main()
{// input;int num;cin>>num;while(num--){vector<vector<int>> input_tree;int depth;cin>>depth;for(int i=1; i<=depth; i++){vector<int> tmp;int input;for(int j=0; j<i; j++){cin>>input;tmp.push_back(input);}input_tree.push_back(tmp);}// // debug_input// output(input_tree);solution mySolve;int res = mySolve.getMaxPathSum(input_tree);cout<<res<<endl;}return 0;
}

（二）后序DFS（自底向上搜索，设置memory数组记录各节点子树的最大路径和，相同子树剪枝优化，AC）

（1）递归无返回值

#include<iostream>
#include<vector>
using namespace std;void debug_input(vector<vector<int>>& input){for(int i=0; i<input.size(); i++){for(auto it=input[i].begin(); it!=input[i].end(); it++){cout<<*it<<" ";}cout<<endl;}
}class solution
{
private:vector<vector<int>> memory;// 记录每个子树maxSum// 从下至上遍历->后序->相同子树剪枝void traversal(vector<vector<int>>& input, int depth, int width){// 终止条件->遇叶节点if(depth == input.size()-1){memory[depth][width] = input[depth][width];return;}// 遇相同子树->剪枝if(memory[depth][width]) return;// 后序遍历// lefttraversal(input, depth+1, width);// righttraversal(input, depth+1, width+1);// midmemory[depth][width] = input[depth][width] + max(memory[depth+1][width], memory[depth+1][width+1]);}
public:int getMaxPathSum(vector<vector<int>>& input){vector<int> vec(input.size(), 0);memory.resize(input.size(), vec);traversal(input, 0, 0);return memory[0][0];}
};int main()
{int num;cin>>num;while(num--){vector<vector<int>> input;int depth;cin>>depth;for(int i=1; i<=depth; i++){vector<int> tmp;for(int j=0; j<i; j++){int in;cin>>in;tmp.push_back(in);}input.push_back(tmp);}// debug_input(input);solution my_solve;int res = my_solve.getMaxPathSum(input);cout<<res<<endl;}return 0;
}

（2）递归有返回值

#include<iostream>
#include<vector>
using namespace std;void debug_input(vector<vector<int>>& input){for(int i=0; i<input.size(); i++){for(auto it=input[i].begin(); it!=input[i].end(); it++){cout<<*it<<" ";}cout<<endl;}
}class solution
{
private:vector<vector<int>> memory;// 记录每个子树maxSum// 从下至上遍历->后序->相同子树剪枝int traversal(vector<vector<int>>& input, int depth, int width){// 终止条件->遇叶节点if(depth >= input.size()-1){return input[depth][width];}// 遇相同子树->剪枝if(memory[depth][width]) return memory[depth][width];// 后序遍历// leftint left_sum = traversal(input, depth+1, width);// rightint right_sum = traversal(input, depth+1, width+1);// midmemory[depth][width] = input[depth][width] + max(left_sum, right_sum);return memory[depth][width];}
public:int getMaxPathSum(vector<vector<int>>& input){vector<int> vec(input.size(), 0);memory.resize(input.size(), vec);int res = traversal(input, 0, 0);return res;}
};int main()
{int num;cin>>num;while(num--){vector<vector<int>> input;int depth;cin>>depth;for(int i=1; i<=depth; i++){vector<int> tmp;for(int j=0; j<i; j++){int in;cin>>in;tmp.push_back(in);}input.push_back(tmp);}// debug_input(input);solution my_solve;int res = my_solve.getMaxPathSum(input);cout<<res<<endl;}return 0;
}