让我们再次考虑二阶线性系统
d Y d t = A Y \frac{d\mathbf{Y}}{dt}=A\mathbf{Y} dtdY=AY
我们已经知道,分析这种二阶系统。最主要的是注意它的特征值情形。
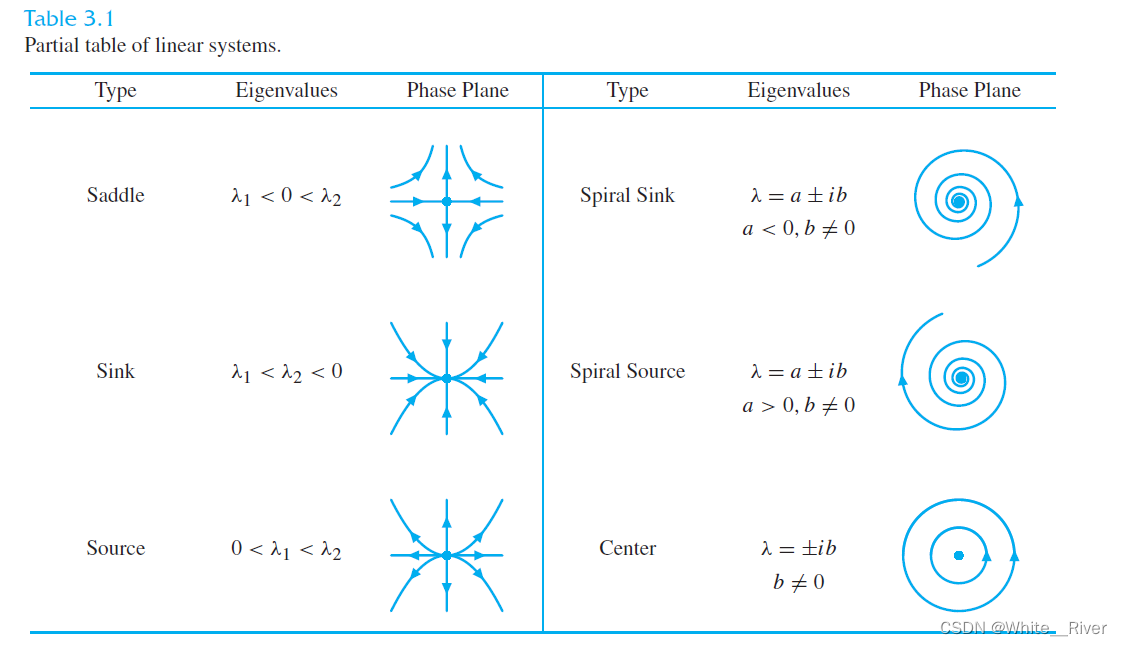
(此处没有重根的情形,所有是partial)
而特征值,也就是系统矩阵特征方程的根,和而系统矩阵是直接相关的。
我们知道,在线性代数理论中,矩阵A的迹Trace(A)(简称Tr)是A的各个特征值之和,而矩阵A的行列式determinant(A)(简称det)为特征值的积。
这里我们只考虑二阶系统。
1. 利用矩阵的迹-行列式求特征值
因此若A的特征值为 λ 1 , λ 2 \lambda_1, \lambda_2 λ1,λ2 则有
λ 1 + λ 2 = T r ( A ) λ 1 ∗ λ 2 = d e t ( A ) \lambda_1 + \lambda_2= Tr(A)\\ \lambda_1 * \lambda_2=det(A) λ1+λ2=Tr(A)λ1∗λ2=det(A)
上过初中的朋友,如果考虑到特征值就是系统矩阵特征方程的根,会不会让你回忆起韦达定理: 对于方程 a λ 2 + b λ + c = 0 a \lambda^2+b\lambda+c=0 aλ2+bλ+c=0:
λ 1 + λ 2 = − b a λ 1 ∗ λ 2 = c a \lambda_1 + \lambda_2= -\frac{b}{a}\\ \lambda_1 * \lambda_2=\frac{c}{a} λ1+λ2=−abλ1∗λ2=ac
利用 T r ( A ) 和 d e t ( A ) 和 a , b , c Tr(A)和det(A)和a, b, c Tr(A)和det(A)和a,b,c的关系, 再根据二次方程求根公式, 有
λ 1 , 2 = T r ± T r 2 − 4 ∗ d e t 2 \lambda_{1,2} = \frac{Tr±\sqrt{Tr^2-4*det}}{2} λ1,2=2Tr±Tr2−4∗det
A被省略掉了
因此, 我们利用矩阵A的迹-行列式, 直接求系统特征值, 进而判断系统解的形态, 而不必列出特征方程, 这是一个比较巧妙的方法.
下面, 我们介绍一个必杀技, 如何一眼秒杀解的形态.
2. 利用矩阵的迹-行列式直接分析系统解的形态
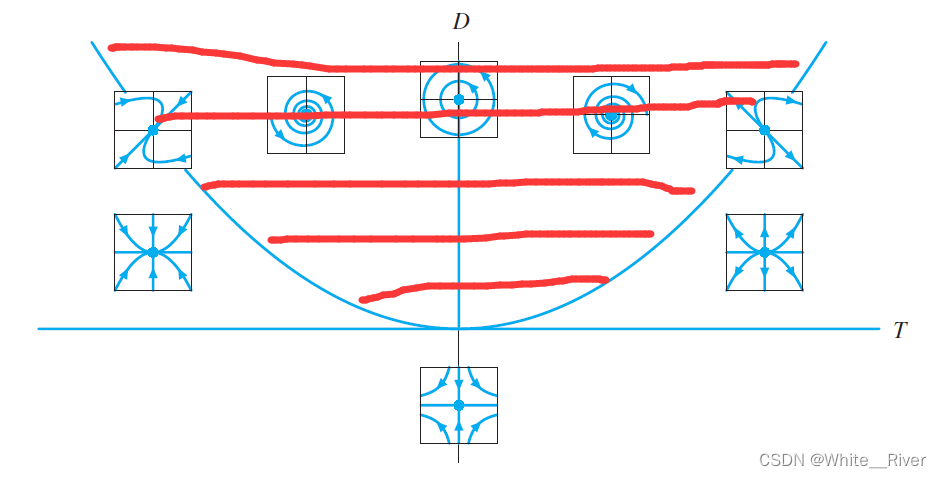
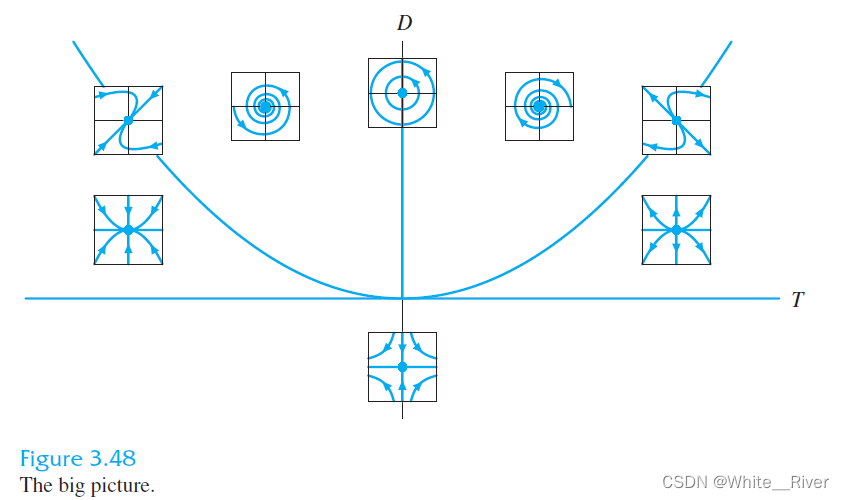 T代表trace,D代表行列式.
T代表trace,D代表行列式.
这个图你一看1应该有点感觉了,下面我来讲一下这个图.
回顾上面的公式
λ 1 , 2 = T ± T 2 − 4 ∗ D 2 \lambda_{1,2} = \frac{T±\sqrt{T^2-4*D}}{2} λ1,2=2T±T2−4∗D
2.1 两个不同实根 T 2 − 4 ∗ D > 0 T^2-4*D>0 T2−4∗D>0
我们看到 T 2 − 4 ∗ D > 0 T^2-4*D>0 T2−4∗D>0的情况,也就像下面图的红色区域,代表系统有两个不一样的实特征值
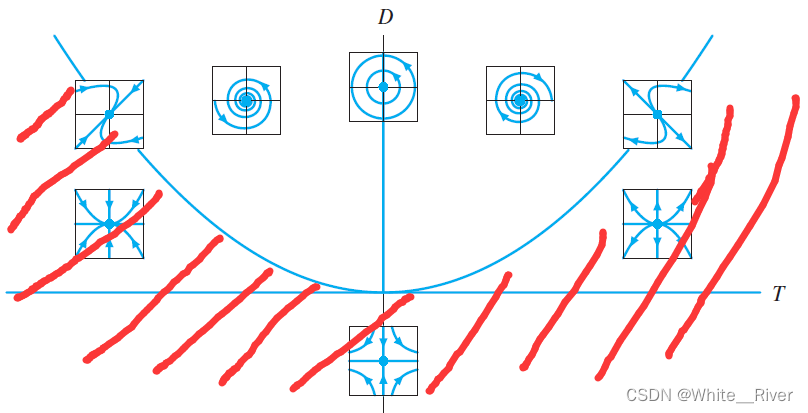 由于
由于
λ 1 + λ 2 = T λ 1 ∗ λ 2 = D \lambda_1 + \lambda_2= T\\ \lambda_1 * \lambda_2=D λ1+λ2=Tλ1∗λ2=D
因此当 T < 0 , D > 0 T<0, D>0 T<0,D>0,代表系统两个负特征值,此时平衡点为sink
当 T < 0 , D < 0 T<0, D<0 T<0,D<0,代表系统两个特征值一正一负,此时平衡点为saddle
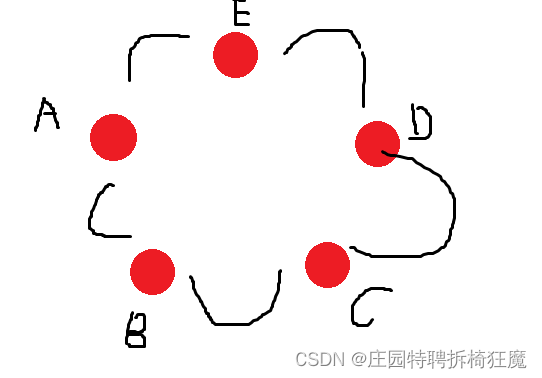
当 T < 0 , D = 0 T<0, D=0 T<0,D=0,代表系统两个特征值一个负一个0,此时平衡点为node, 系统只有一个直线解, 相图的形状大概长这样
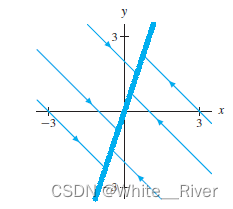 负特征值对应的一个特征空间 0特征值对应另外一个特征空间
负特征值对应的一个特征空间 0特征值对应另外一个特征空间
这两个特征空间的直和构成整个相平面
如果系统的初始状态落在负特征值对应的特征空间上,则会沿着特征向量的方向趋近于原点/平衡点
如果系统的初始状态落在0特征值对应的特征空间上,它就不动了,换言之, 0特征值对应的特征空间构成了系统的一个不变集,每个点都是平衡点(学过非线性系统的同学们!)
如果初始状态落在其他地方,由于线性代数告诉我们,初始状态可以在两个分量上投影,对应负特征值方向的分量会收敛为0, 而对应0特征值方向的分量则不动了。
T > 0 T>0 T>0的情况也可以类似的推出来
2.2 一对纯虚根 T 2 − 4 ∗ D < 0 T^2-4*D<0 T2−4∗D<0
 这个就不用多说了吧
这个就不用多说了吧
由于两个根实部相同
T > 0 T>0 T>0必定是不稳定的spiral source
T < 0 T<0 T<0必定是稳定的spiral sink
T = 0 T=0 T=0则是无阻尼振荡的螺旋center
2.3 最抽象的情况 重根 T 2 − 4 ∗ D = 0 T^2-4*D=0 T2−4∗D=0
这在迹-行列式平面中表现为一条二次曲线
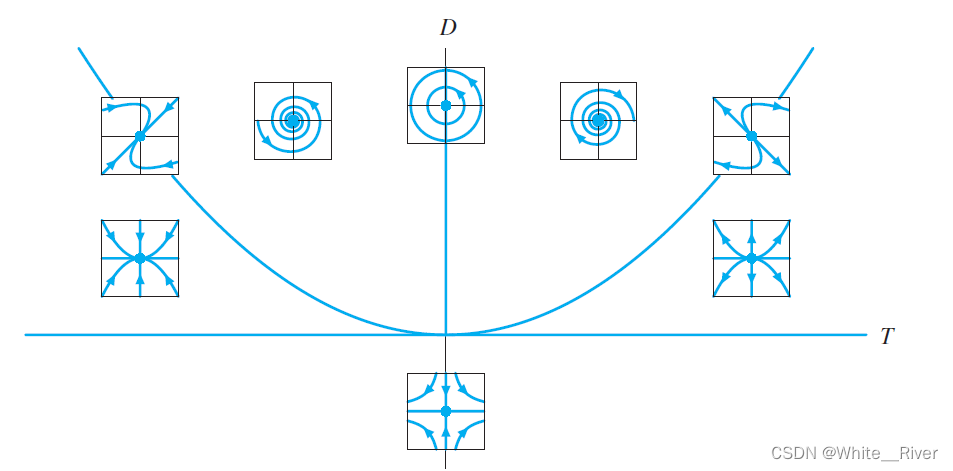 显然, T > 0 T>0 T>0必定是不稳定的node
显然, T > 0 T>0 T>0必定是不稳定的node
T < 0 T<0 T<0必定是稳定的node
T = 0 T=0 T=0就是原点,啥也没有
综上所述,你学会trace-determinant method了吗?



![C语言辨析——声明int a[3][6], a[0][9]越界吗?](https://img-blog.csdnimg.cn/img_convert/31ee1f99ef84f30b513d55069f3f04f5.png)