本专题主要介绍在求序列的经典问题上dp的应用。
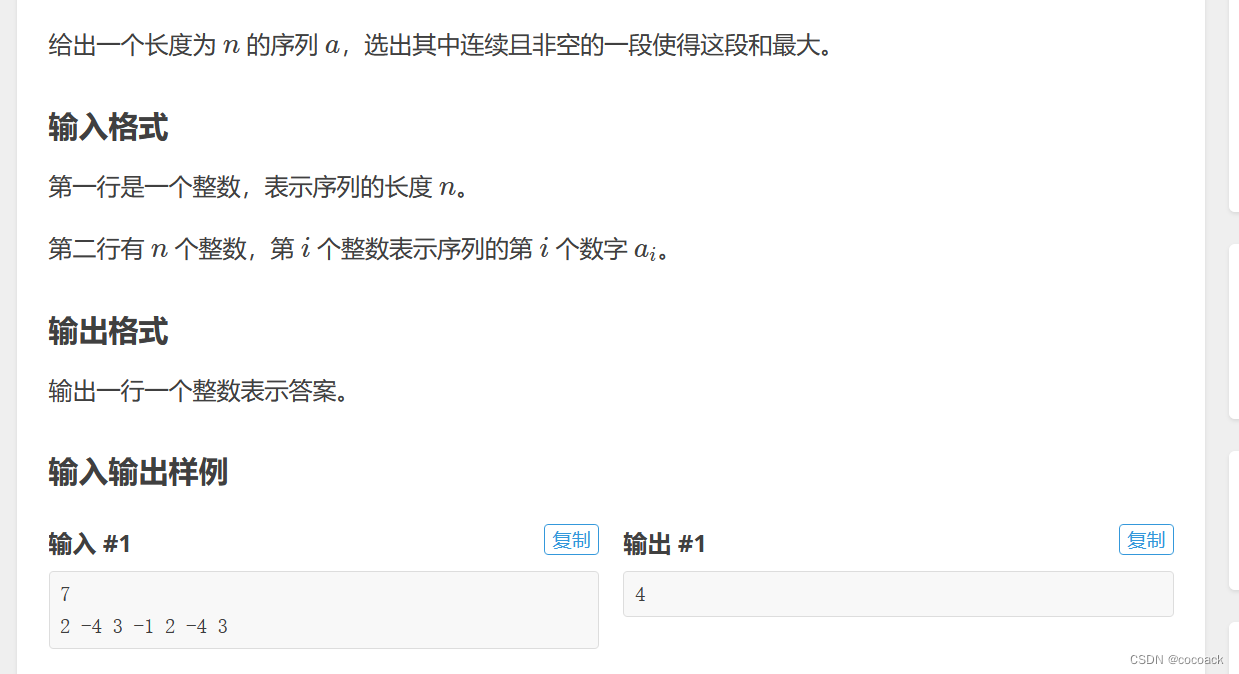
我们上次用前缀和来解决,这次让我们用dp解决把
我们参考不下降子序列的思路,可以令f[i]为以i结尾的最大字段和,易得:
f[i]=max(a[i],a[i]+f[i-1]);
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int a[200010],dp[200010],n,ans=-9999999;
int main(){cin>>n;for(int i=1;i<=n;i++) scanf("%d",&a[i]);dp[1]=a[1];for(int i=2;i<=n;i++){dp[i]=max(a[i],a[i]+dp[i-1]);ans=max(ans,dp[i]);}ans=max(ans,dp[1]);cout<<ans;
}接题:

因为是求两个序列,我们把dp弄成二维。
我们令f[i][j]为第一个序列前i个与第二个序列前j个的最长公共子序列。
我们可以得出:当两个序列后面加了一个数,那么如果用到了其中一个,那么那个子序列一定就结束了,因为如果后面还有的话其中一个序列一定不符合(因为它后面已经没数了)
根据这个,我们知道如果加的数不同,相当于只有其中一个发挥作用,我们取两个max即可
于是,当s1[i]==s2[j]时f[i][j]=1+f[i-1][j-1];
当s1[i]!=s2[j]时 f[i][j]=max(f[i-1][j],f[i][j-1])
对于初始条件
s1[1]==s2[1] f[1][1]=1;
s1[1]!=s2[1] f[1][1]=0;
下面是AC代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
using namespace std;
string s1,s2;
int dp[1000][1000];
int main(){while(cin>>s1>>s2){memset(dp,0,sizeof(dp));for(int i=1;i<=s1.length();i++){for(int j=1;j<=s2.length();j++){if(s1[i-1]==s2[j-1]) dp[i][j]=1+dp[i-1][j-1];else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}printf("%d\n",dp[s1.length()][s2.length()]);}
}