一、引言
在图论和树形结构中,搜索算法是寻找从起点到终点的路径的关键。其中,深度优先搜索(DFS)和广度优先搜索(BFS)是最常用且最基础的两种搜索算法。本文将详细介绍广度优先搜索(BFS)的原理、应用场景,并通过代码示例来展示其实现。

二、广度优先搜索(BFS)简介
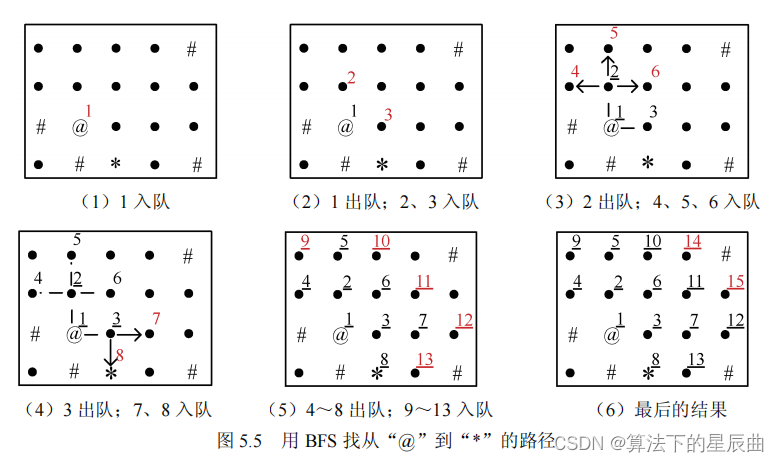
广度优先搜索(BFS)是一种用于遍历或搜索树或图的算法。它从根(或任意节点)开始,探索最近的节点,然后进行下一层的邻居节点,逐层向外扩展。这种策略使得BFS能够首先找到从起始点到目标点的最短路径(如果存在的话)。
三、BFS算法步骤
- 创建一个队列,并将起始节点入队。
- 从队列中取出一个节点,并检查它是否为目标节点。如果是,则搜索结束,返回路径。
- 如果不是目标节点则将其所有未访问过的邻居节点入队并标记这些邻居节点为已访问。
- 重复步骤2和3,直到队列为空或者找到目标节点。
四、BFS的应用场景
- 最短路径问题:在图中查找从源点到目标点的最短路径。
- 图的遍历:访问图中的所有节点。
- 迷宫求解:在迷宫中找到从起点到终点的路径。
五、BFS代码示例(Python)
下面是一个简单的BFS实现,用于在无向图中搜索路径:
from collections import deque def bfs(graph, start, end): visited = set() queue = deque([start]) while queue: vertex = queue.popleft() if vertex == end: return True for neighbour in graph[vertex]: if neighbour not in visited: visited.add(neighbour) queue.append(neighbour) return False # 示例图(使用邻接表表示)
graph = { 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E'],
} # 测试BFS函数
print(bfs(graph, 'A', 'F')) # 输出: True
print(bfs(graph, 'A', 'D')) # 输出: True
print(bfs(graph, 'A', 'G')) # 输出: False在这个示例中,我们定义了一个
bfs函数,它接受一个图(以邻接表形式表示)、一个起始节点和一个目标节点作为输入。函数使用队列来存储待访问的节点,并使用一个集合来跟踪已访问的节点。如果找到目标节点,函数返回True;否则,返回False。