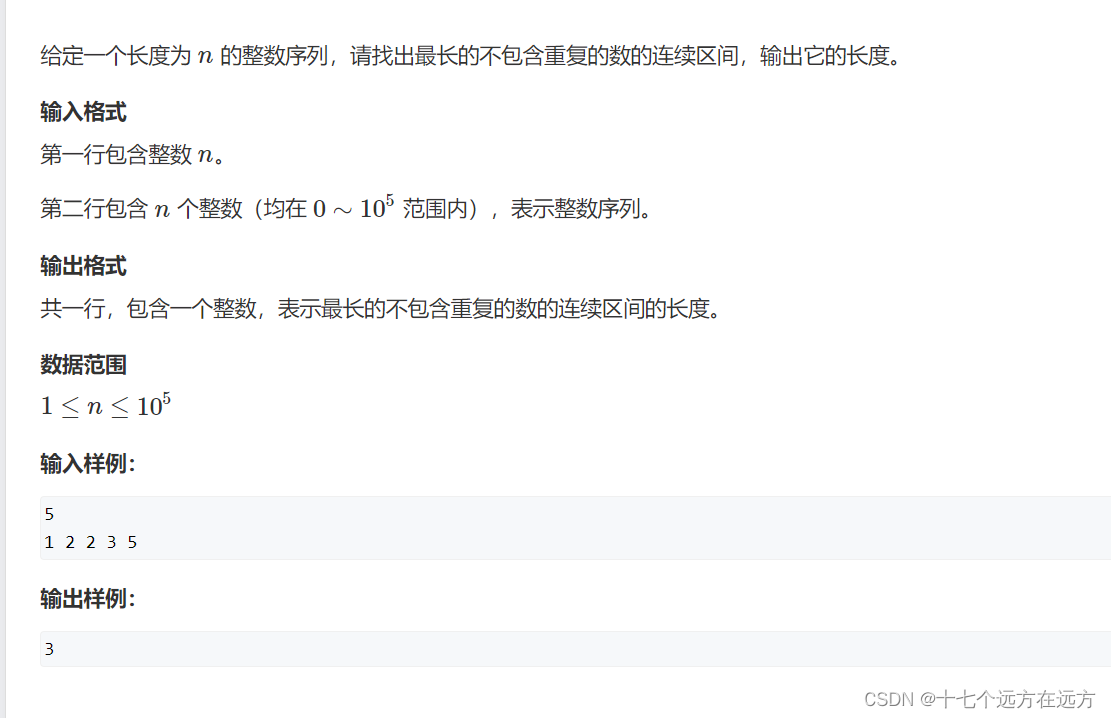
对于几种常用的排序算法,无论是归并排序、快速排序、以及更加常见的冒泡排序等,这些排序算法的时间复杂度都是大于等于O(n*lg(n))的,而这些排序算法存在一个共同的行为,那就是这些算法在对元素进行排序的时候,都会进行同一个操作,也就是对数组中取出文件,然后会对取出来的这两个元素进行相互比较。
而针对这个,我们是可以从理论上进行证明,也就是任何的排序算法,只要这个排序算法会存在一个取出元素的动作,那就会存在以上的结论,时间复杂度大于等于O(n*lg(n)),例如在冒泡排序中,依次取出 两个元素,对这个元素进行比较大小,然后调整被比较元素的位置。在归并排序中,将数组分为两个子数组进行排序,然后依次从两个排好序的数组中取出元素进行比较以便将他们合并成为一个元素。在堆排序中,每次往堆中增加一个新元素的时候,它都必须与父节点比较,然后根据比较之后的大小来和父节点进行位置的调换。而在快速排序中,选中一个pivot元素的话,其他元素就需要与该元素进行比较,以此来进行位置调换。
只要将两个元素进行比较,那必然会执行三个测试,也即是a<b,a>b,a=b的行为,由此会得出两个元素的相对位置,如果将等于这个行为与其中一个行为合并之后,该测试行为会被简化为两个行为,也就是a<=b或者是a>b,也就是说,元素比较的的结果会产生两个可能,大于或者小于等于,类比为比较行为当成是一个父节点,可能会产生的两个孩子节点:

添加图片注释,不超过 140 字(可选)
而如果将排序算法中每一次的比较用图表示,那么就会得到一个二叉树结构,冒泡排序的结果:

添加图片注释,不超过 140 字(可选)

添加图片注释,不超过 140 字(可选)
将所有可能性展开之后,就会得到如上图所示的二叉树模型,改模型也叫作决策树模型,在叶子节点中列出了元素排列的所有可能性,因此数组排序之后,其元素的排列一定属于叶子节点所表示的某一种情况。
由此基于元素比较的排序算法,本质上是从顶层根节点开始,沿着左边或者右边的某个分支一直走到底层某个节点。
分析叶子节点的数量与高度的关系,由于一个父节点可以衍生出来两个孩子节点,因此每下降一层的话,节点的数量就是上一层的两倍,如果决策树的高度使用h表示的话,就可以得出叶子节点数量是最多是2的h次方个。
每个节点对应元素的一种排列方式的话,那如果数组会有n个节点,那么节点排列的可能性总共有n的阶乘中,也就是说,决策树底层会有n的阶乘个叶子结点,由于决策树底层叶子结点对应的元素排好序之后的排列,依次决策树的叶子节点必须大于等于n的阶乘。
从这里就可以得出结论,时间复杂度大于等于O(n*lg(n))。