n 位格雷码序列 是一个由 2n 个整数组成的序列,其中:
- 每个整数都在范围
[0, 2n - 1]内(含0和2n - 1) - 第一个整数是
0 - 一个整数在序列中出现 不超过一次
- 每对 相邻 整数的二进制表示 恰好一位不同 ,且
- 第一个 和 最后一个 整数的二进制表示 恰好一位不同
给你一个整数 n ,返回任一有效的 n 位格雷码序列 。
示例 1:
输入:n = 2 输出:[0,1,3,2] 解释: [0,1,3,2] 的二进制表示是 [00,01,11,10] 。 - 00 和 01 有一位不同 - 01 和 11 有一位不同 - 11 和 10 有一位不同 - 10 和 00 有一位不同 [0,2,3,1] 也是一个有效的格雷码序列,其二进制表示是 [00,10,11,01] 。 - 00 和 10 有一位不同 - 10 和 11 有一位不同 - 11 和 01 有一位不同 - 01 和 00 有一位不同
示例 2:
输入:n = 1 输出:[0,1]
解法一 动态规划
按照动态规划或者说递归的思路去想,也就是解决了小问题,怎么解决大问题。
我们假设我们有了 n = 2 的解,然后考虑怎么得到 n = 3 的解。
n = 2 的解
00 - 0
10 - 2
11 - 3
01 - 1
如果再增加一位,无非是在最高位增加 0 或者 1,考虑先增加 0。由于加的是 0,其实数值并没有变化。
n = 3 的解,最高位是 0
000 - 0
010 - 2
011 - 3
001 - 1
再考虑增加 1,在 n = 2 的解基础上在最高位把 1 丢过去?
n = 3 的解
000 - 0
010 - 2
011 - 3
001 - 1
------------- 下面的是新增的
100 - 4
110 - 6
111 - 7
101 - 5
似乎没这么简单哈哈,第 4 行 001 和新增的第 5 行 100,有 3 个 bit 位不同了,当然不可以了。怎么解决呢?
很简单,第 5 行新增的数据最高位由之前的第 4 行的 0 变成了 1,所以其它位就不要变化了,直接把第 4 行的其它位拉过来,也就是 101。
接下来,为了使得第 6 行和第 5 行只有一位不同,由于第 5 行拉的第 4 行的低位,而第 4 行和第 3 行只有一位不同。所以第 6 行可以把第 3 行的低位拿过来。其他行同理,如下图。
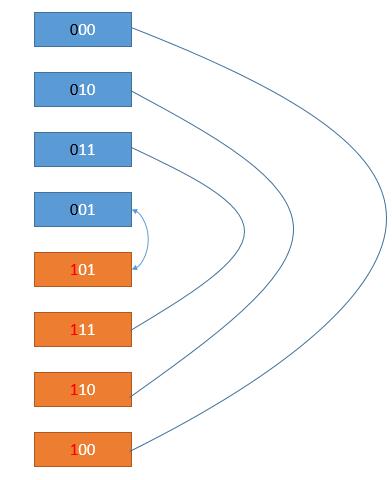
蓝色部分由于最高位加的是 0 ,所以它的数值和 n = 2 的所有解的情况一样。而橙色部分由于最高位加了 1,所以值的话,就是在其对应的值上加 4,也就是 2222,即23−123−1,也就是 1 << ( n - 1) 。所以我们的算法可以用迭代求出来了。
所以如果知道了 n = 2 的解的话,如果是 { 0, 1, 3, 2},那么 n = 3 的解就是 { 0, 1, 3, 2, 2 + 4, 3 + 4, 1 + 4, 0 + 4 },即 { 0 1 3 2 6 7 5 4 }。之前的解直接照搬过来,然后倒序把每个数加上 1 << ( n - 1) 添加到结果中即可。
public List<Integer> grayCode(int n) {List<Integer> gray = new ArrayList<Integer>();gray.add(0); //初始化 n = 0 的解for (int i = 0; i < n; i++) {int add = 1 << i; //要加的数//倒序遍历,并且加上一个值添加到结果中for (int j = gray.size() - 1; j >= 0; j--) {gray.add(gray.get(j) + add);}}return gray;
}
时间复杂度:O(2n),因为有这么多的结果。
空间复杂度:O(1)。
解法二 直接推导
解法一我觉得,在不了解格雷码的情况下,还是可以想到的,下边的话,应该是之前了解过格雷码才写出来的。看下维基百科提供的一个生成格雷码的思路。
以二进制为 0 值的格雷码为第零项,第一项改变最右边的位元,第二项改变右起第一个为1的位元的左边位元,第三、四项方法同第一、二项,如此反复,即可排列出n个位元的格雷码。
以 n = 3 为例。
0 0 0 第零项初始化为 0。
0 0 1 第一项改变上一项最右边的位元
0 1 1 第二项改变上一项右起第一个为 1 的位元的左边位
0 1 0 第三项同第一项,改变上一项最右边的位元
1 1 0 第四项同第二项,改变最上一项右起第一个为 1 的位元的左边位
1 1 1 第五项同第一项,改变上一项最右边的位元
1 0 1 第六项同第二项,改变最上一项右起第一个为 1 的位元的左边位
1 0 0 第七项同第一项,改变上一项最右边的位元
思路有了,代码自然也就出来了。
public List<Integer> grayCode2(int n) {List<Integer> gray = new ArrayList<Integer>();gray.add(0); //初始化第零项for (int i = 1; i < 1 << n; i++) {//得到上一个的值int previous = gray.get(i - 1);//同第一项的情况if (i % 2 == 1) {previous ^= 1; //和 0000001 做异或,使得最右边一位取反gray.add(previous);//同第二项的情况} else {int temp = previous;//寻找右边起第第一个为 1 的位元for (int j = 0; j < n; j++) {if ((temp & 1) == 1) {//和 00001000000 类似这样的数做异或,使得相应位取反previous = previous ^ (1 << (j + 1));gray.add(previous);break;}temp = temp >> 1;}}}return gray;
}
解法三 公式
二进制转成格雷码有一个公式。
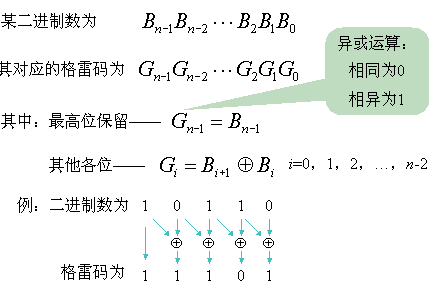
所以我们遍历 0 到 2�−12n−1,然后利用公式转换即可。即最高位保留,其它位是当前位和它的高一位进行异或操作。
public List<Integer> grayCode(int n) {List<Integer> gray = new ArrayList<Integer>();for(int binary = 0;binary < 1 << n; binary++){gray.add(binary ^ binary >> 1);}return gray;
}