【计算几何】给定一组点的多边形面积-编程知识

【计算几何】给定一组点的多边形面积

一、说明

计算多边形面积的方法有很多种。众所周知的多边形（如三角形、矩形、正方形、梯形等）的面积可以使用简单的数学公式计算。在这篇文章中，我将讨论如何计算给定顶点集的多边形面积。这里讨论的方法适用于大多数没有孔的多边形。

二、有序顶点集

如果多边形的顶点按顺时针或逆时针方向排列，则可以使用鞋带算法计算面积。该公式可以用表达式表示

$\frac{1}{2}\left|\sum_{i = 1}^{n-1}x_iy_{i+1}+x_ny_1 - \sum_{i = 1}^{n - 1}x_{i + 1}y_i - x_1y_n\right|$

使用此公式的唯一条件是顶点必须按顺时针或逆时针方向排序，否则面积将不正确。这是该算法的Python实现。

# Shoelace formula to calculate the area of a polygon
# the points must be sorted anticlockwise (or clockwise)def polygon_area(vertices):psum = 0nsum = 0for i in range(len(vertices)):sindex = (i + 1) % len(vertices)prod = vertices[i].x * vertices[sindex].ypsum += prodfor i in range(len(vertices)):sindex = (i + 1) % len(vertices)prod = vertices[sindex].x * vertices[i].ynsum += prodreturn abs(1/2*(psum - nsum))

列表顶点包含 Point 类型的对象列表。点是表示 2D 平面中的点的数据结构。表示一个点的Python代码是

class Point:def __init__(self, x, y):self.x = xself.y = ydef __str__(self):return '(' + str(self.x) + ', ' + str(self.y) + ')'

下面的代码片段测试了上面的代码。

if __name__ == '__main__':points = [Point(0, 0), Point(5, 0), Point(5, 5), Point(0, 5)]print polygon_area(points) # prints 25

三、无序顶点集

如果顶点不是顺时针或逆时针排列的，那么计算面积可能会有点棘手。这意味着，在调用之前，我们需要按顺时针或逆时针polygon_area(points)排序。points为了对顶点进行排序，我们需要一个完全位于多边形内部的参考点。有了参考点后，我们计算参考点与每个顶点之间的角度，并按升序或降序对它们进行排序。现在的问题是，我们如何找到参考点呢？答案很简单“这取决于多边形的类型”。

3.1 凸多边形

如果多边形是凸多边形，即所有内角都小于或等于的多边形18001800，多边形内的任何点都可以是给出完全相同面积的参考点，即无论参考点位于多边形内的哪个位置，面积在所有情况下都是相同的。这是因为参考点的选择不会改变凸多边形的形状。在这种情况下，我们可以简单地平均X 和y 坐标来找到参考点。这可以很容易地计算出来，如下面的代码所示。

# returns the average x and y coordinates of all the points
def average_point_inside(points):x = 0y = 0for point in points:x += point.xy += point.yreturn Point(x / len(points), y / len(points))

3.2 非凸多边形

对于非凸多边形，参考点的选择会改变多边形的形状，因此不同的参考点可能会得到不同的面积。因此，如果多边形不是凸多边形，那么在顶点未排序的情况下求面积没有任何意义。

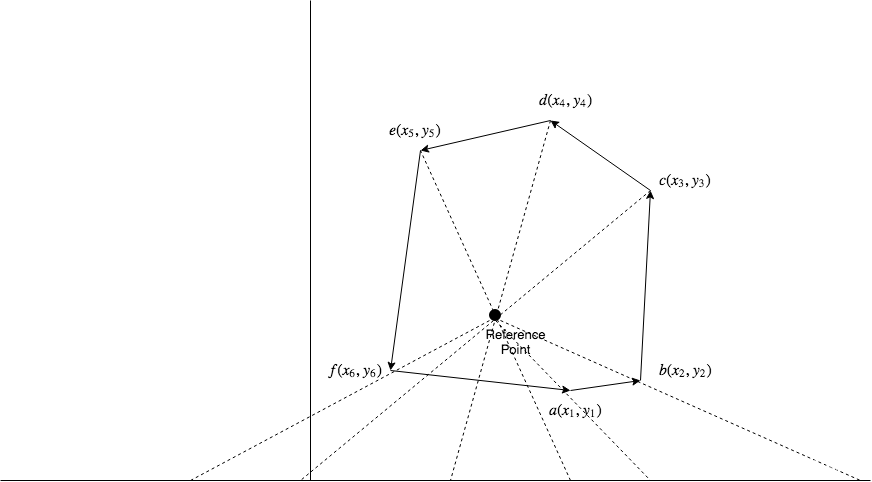
一旦我们有了参考点（仅对凸多边形有意义），我们就可以根据参考点与每个顶点与 x 轴逆时针方向连接的线段所成的角度对所有顶点进行排序如下图所示，下面的代码计算参考点和顶点与x轴的连线之间的角度（以弧度为单位）。
在这里插入图片描述

# returns the angle made by a line segment
# connecting p1 and p2 with x-axis in the anticlockwise direction
def angle(p1, p2):k = (p2.y - p1.y) / distance(p1, p2)x2 = p2.xx1 = p1.xif k >= 0:if x2 >= x1: # First Quadrantreturn (2.0 * math.pi - math.asin(k))else: # Second Quadrantreturn (math.pi + math.asin(k))else:if x2 >= x1: # Fourth Quadrantreturn math.asin(-k)else: # Third Quadrantreturn (math.pi - math.asin(-k))

sorted我们可以使用标准Python库的方法对顶点进行排序。这里的技巧是我们传递根据角度比较点的比较器。

# angularly sort the points anticlockwise
def sort_angular(points, reference_point):return sorted(points, key = lambda point: -angle(point, reference_point))

现在我们完成了。我们将排序后的点传递到polygon_area给出正确面积的函数中。下面的代码片段测试了上面的代码。

if __name__ == '__main__':points = [Point(0,3), Point(2, 4), Point(3,1), Point(4,3), Point(3, 5), Point(1, 1)]reference_point = average_point_inside(points)spoints =  sort_angular(points, reference_point)print polygon_area(spoints) # prints 9