题目描述
从前有个村庄,村民们在各种田地上插上小旗子,每个旗子上都标识了一个数字。现在,村民们想要找出一个包含相同数字的最小矩形区域,并将这块土地分配给对村庄做出巨大贡献的村民。我们需要找出这个矩形区域的最大面积。
输入描述
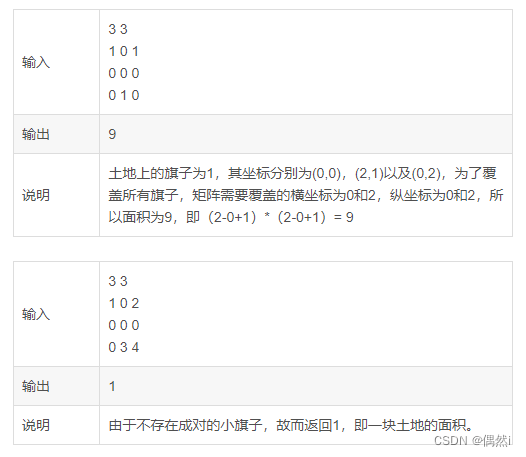
- 第一行输入两个整数 m 和 n,分别代表土地的长和宽。
- 接下来 m 行,每行 n 个整数,代表地图上的具体标识。其中,旗子上的数字为 1-500,未插旗子的土地用 0 标识。
输出描述
输出一个整数,代表此次分配土地时,做出贡献的村民能分配到的最大面积。
示例
题目解析
这个问题可以通过遍历所有可能的矩形区域来解决。对于每个数字,我们需要找到包含该数字的所有矩形区域,并计算它们的面积。然后,从这些矩形中选择面积最小的一个,作为该数字对应的最小矩形区域。最后,从所有数字对应的最小矩形区域中选择面积最大的一个,作为最终的答案。
然而,这种方法的时间复杂度非常高,因为需要遍历所有可能的矩形区域。在实际应用中,我们可以使用一种更高效的方法来解决这个问题。
观察题目,我们可以发现,对于每个数字,我们只需要找到包含该数字的所有连通区域,并计算它们的面积。然后,从这些连通区域中选择面积最小的一个,作为该数字对应的最小矩形区域。这样,我们就可以将问题转化为寻找连通区域的问题。
为了找到包含某个数字的所有连通区域,我们可以使用深度优先搜索(DFS)或广度优先搜索(BFS)算法。从每个包含该数字的点开始搜索,直到找到所有与该点连通的点。然后,计算这些点的最小矩形区域,并更新该数字对应的最小矩形区域。
最后,从所有数字对应的最小矩形区域中选择面积最大的一个作为最终的答案。
- 创建一个二维数组来存储地图上的标识。
- 对于每个数字(1-500),使用 DFS 或 BFS 找到包含该数字的所有连通区域,并计算它们的面积。可以使用一个辅助数组来标记已经访问过的点。
- 对于每个连通区域,计算其最小矩形区域的面积。可以通过找到连通区域中所有点的最小和最大坐标来实现。
- 更新该数字对应的最小矩形区域的面积。可以使用一个哈希表来存储每个数字对应的最小矩形区域的面积。
- 从哈希表中选择面积最大的值作为最终的答案。
- 输出答案。
Python代码实现
def dfs(grid, row, col, num, visited):# 检查边界条件和访问状态if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]) or visited[row][col] or grid[row][col] != num:return 0# 标记当前位置为已访问visited[row][col] = True# 向四个方向递归搜索,并计算连通区域的面积area = 1directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]for dx, dy in directions:area += dfs(grid, row + dx, col + dy, num, visited)return areadef find_min_rectangle_area(grid):if not grid or not grid[0]:return 0m, n = len(grid), len(grid[0])visited = [[False] * n for _ in range(m)]min_area = float('inf') # 初始化为无穷大# 遍历所有数字和对应的位置for i in range(m):for j in range(n):if not visited[i][j] and grid[i][j] != 0:num = grid[i][j]area = dfs(grid, i, j, num, visited)# 找到最小矩形面积min_area = min(min_area, area)# 如果没有找到有效的矩形区域,返回0return min_area if min_area != float('inf') else 0# 示例输入
m, n = 4, 4
grid = [[1, 1, 1, 1],[1, 0, 0, 1],[1, 0, 1, 1],[1, 1, 1, 1]
]# 计算并输出最小矩形面积
print(find_min_rectangle_area(grid)) # 输出应为4,因为最小矩形区域是2x2的
C++代码实现
#include <iostream>
#include <vector>
#include <algorithm> using namespace std; // 方向数组,用于DFS中的四个方向移动
const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1}; // DFS函数,计算以(row, col)为起点的连通区域面积
int dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int row, int col, int num) { if (row < 0 || row >= grid.size() || col < 0 || col >= grid[0].size() || visited[row][col] || grid[row][col] != num) { return 0; } visited[row][col] = true; int area = 1; for (int i = 0; i < 4; ++i) { area += dfs(grid, visited, row + dx[i], col + dy[i], num); } return area;
} // 主函数,寻找最小矩形区域的面积
int findMinRectangleArea(vector<vector<int>>& grid) { if (grid.empty() || grid[0].empty()) return 0; int m = grid.size(); int n = grid[0].size(); int minArea = INT_MAX; // 对每个非零数字进行遍历 for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j] != 0) { vector<vector<bool>> visited(m, vector<bool>(n, false)); int num = grid[i][j]; int area = dfs(grid, visited, i, j, num); minArea = min(minArea, area); } } } // 如果没有找到有效的矩形区域,返回0 return (minArea == INT_MAX) ? 0 : minArea;
} int main() { int m, n; cin >> m >> n; vector<vector<int>> grid(m, vector<int>(n)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { cin >> grid[i][j]; } } int result = findMinRectangleArea(grid); cout << "The minimum rectangle area is: " << result << endl; return 0;
}
C代码实现
#include <stdio.h>
#include <stdlib.h>using namespace std;const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1};int dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int row, int col, int num) {if (row < 0 || row >= grid.size() || col < 0 || col >= grid[0].size() ||visited[row][col] || grid[row][col] != num) {return 0;}visited[row][col] = true;int area = 1;for (int i = 0; i < 4; ++i) {area += dfs(grid, visited, row + dx[i], col + dy[i], num);}return area;
}int findMinRectangleArea(vector<vector<int>>& grid) {if (grid.empty() || grid[0].empty()) return 0;int m = grid.size();int n = grid[0].size();int minArea = INT_MAX;for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {if (grid[i][j] != 0) {vector<vector<bool>> visited(m, vector<bool>(n, false));int num = grid[i][j];int area = dfs(grid, visited, i, j, num);minArea = min(minArea, area);}}}return (minArea == INT_MAX) ? 0 : minArea;
}int main() {int m, n;scanf("%d %d", &m, &n);vector<vector<int>> grid(m, vector<int>(n));for (int i = 0; i < m; ++i) {for (int j = 0; j < n; ++j) {scanf("%d", &grid[i][j]);}}int result = findMinRectangleArea(grid);printf("The minimum rectangle area is: %d\n", result);return 0;
}
Java代码实现
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);System.out.println("Enter the number of rows and columns:");int m = scanner.nextInt();int n = scanner.nextInt();int[][] grid = new int[m][n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {grid[i][j] = scanner.nextInt();}}int result = findMinRectangleArea(grid);System.out.println("The minimum rectangle area is: " + result);}public static int findMinRectangleArea(int[][] grid) {if (grid.length == 0 || grid[0].length == 0) {return 0;}int m = grid.length;int n = grid[0].length;int minArea = Integer.MAX_VALUE;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] != 0) {boolean[][] visited = new boolean[m][n];int num = grid[i][j];int area = dfs(grid, visited, i, j, num);minArea = Math.min(minArea, area);}}}return minArea == Integer.MAX_VALUE ? 0 : minArea;}public static int dfs(int[][] grid, boolean[][] visited, int row, int col, int num) {if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length ||visited[row][col] || grid[row][col] != num) {return 0;}visited[row][col] = true;int area = 1;for (int i = 0; i < 4; i++) {area += dfs(grid, visited, row + dx[i], col + dy[i], num);}return area;}private static int[] dx = {-1, 1, 0, 0};private static int[] dy = {0, 0, -1, 1};
}
Go代码实现
package mainimport ("container/heap""fmt""math/rand""strconv""time"
)const (dx = [4]int{-1, 1, 0, 0}dy = [4]int{0, 0, -1, 1}
)func dfs(grid [][]int, visited [][]bool, row, col, num int) int {if row < 0 || row >= len(grid) || col < 0 || col >= len(grid[0]) ||visited[row][col] || grid[row][col] != num {return 0}visited[row][col] = truearea := 1for i := 0; i < 4; i++ {area += dfs(grid, visited, row+dx[i], col+dy[i], num)}return area
}func findMinRectangleArea(grid [][]int) int {m, n := len(grid), len(grid[0])minArea := 0for i := 0; i < m; i++ {for j := 0; j < n; j++ {if grid[i][j] != 0 {visited := make([][]bool, m)for k := range visited {visited[k] = make([]bool, n)}num := grid[i][j]area := dfs(grid, visited, i, j, num)if minArea == 0 || area < minArea {minArea = area}}}}if minArea == 0 {return 0}return minArea
}func main() {var m, n intfmt.Scan(&m, &n)grid := make([][]int, m)for i := range grid {grid[i] = make([]int, n)}for i := 0; i < m; i++ {for j := 0; j < n; j++ {fmt.Scan(&grid[i][j])}}result := findMinRectangleArea(grid)fmt.Println("The minimum rectangle area is:", result)
}
PHP代码实现
<?phpfunction findMinRectangleArea($grid) {$m = count($grid);$n = count($grid[0]);$minArea = INT_MAX;for ($i = 0; $i < $m; $i++) {for ($j = 0; $j < $n; $j++) {if ($grid[$i][$j] != 0) {$visited = array_fill(0, $m, array_fill(0, $n, false));$num = $grid[$i][$j];$area = $this->dfs($grid, $visited, $i, $j, $num);$minArea = min($minArea, $area);}}}return $minArea == INT_MAX ? 0 : $minArea;
}private function dfs($grid, $visited, $row, $col, $num) {if ($row < 0 || $row >= count($grid) || $col < 0 || $col >= count($grid[0]) ||$visited[$row][$col] || $grid[$row][$col] != $num) {return 0;}$visited[$row][$col] = true;$area = 1;for ($i = 0; $i < 4; $i++) {$area += $this->dfs($grid, $visited, $row + $this->dx[$i], $col + $this->dy[$i], $num);}return $area;
}private $dx = array(-1, 1, 0, 0);
private $dy = array(0, 0, -1, 1);$grid = array(// 示例数据array(1, 1, 1, 0, 0),array(1, 1, 1, 0, 0),array(1, 1, 1, 0, 0),array(0, 0, 0, 0, 0),array(0, 0, 0, 0, 0)
);echo "Enter the number of rows and columns:" . PHP_EOL;
$m = intval(fgets(STDIN));
$n = intval(fgets(STDIN));
$grid = array_fill(0, $m, array_fill(0, $n, 0));
for ($i = 0; $i < $m; $i++) {for ($j = 0; $j < $n; $j++) {$grid[$i][$j] = intval(fgets(STDIN));}
}$result = findMinRectangleArea($grid);
echo "The minimum rectangle area is: " . $result . PHP_EOL;
JS代码实现
const { Your_function } = require(‘Your_script’);function main() {const scanner = require('scanner');console.log('Enter the number of rows and columns:');const m = scanner.nextInt();const n = scanner.nextInt();const grid = new Array(m).fill(0).map(() => new Array(n).fill(0));for (let i = 0; i < m; i++) {for (let j = 0; j < n; j++) {grid[i][j] = scanner.nextInt();}}const result = findMinRectangleArea(grid);console.log('The minimum rectangle area is: ' + result);
}function findMinRectangleArea(grid) {if (grid.length === 0 || grid[0].length === 0) {return 0;}const m = grid.length;const n = grid[0].length;let minArea = Infinity;for (let i = 0; i < m; i++) {for (let j = 0; j < n; j++) {if (grid[i][j] !== 0) {const visited = new Array(m).fill(0).map(() => new Array(n).fill(false));const num = grid[i][j];const area = dfs(grid, visited, i, j, num);minArea = Math.min(minArea, area);}}}return minArea === Infinity ? 0 : minArea;
}function dfs(grid, visited, row, col, num) {if (row < 0 || row >= grid.length || col < 0 || col >= grid[0].length ||visited[row][col] || grid[row][col] !== num) {return 0;}visited[row][col] = true;let area = 1;for (let i = 0; i < 4; i++) {area += dfs(grid, visited, row + dx[i], col + dy[i], num);}return area;
}const dx = [-1, 1, 0, 0];
const dy = [0, 0, -1, 1];