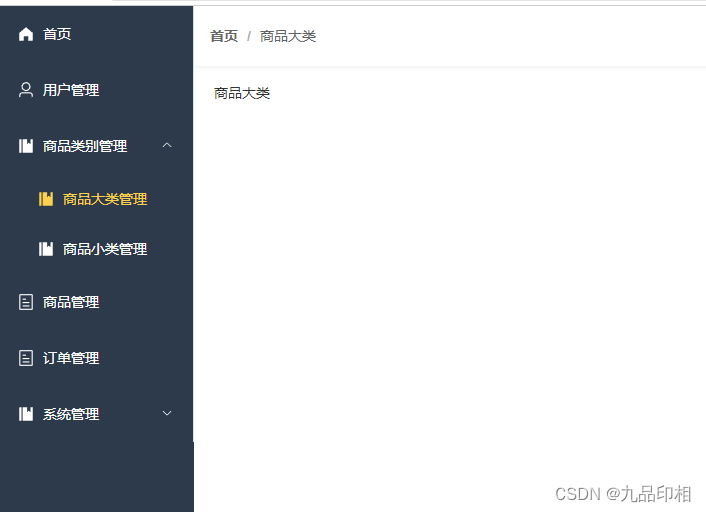
Breadcrumb 面包屑实现

为了实现二级路由，我们搞成搞个子路由，对于二级菜单

const routes = [{path: '/',name: '首页',component: () => import('../views/layout'),redirect:'/home',children:[{path: '/home',name: '首页',component: () => import('../views/home/index')},{path: '/bigType',name: '商品大类',component: () => import('../views/bigType/index')}]},{path: '/login',name: 'login',component: () => import('../views/login')}
]

views/layout/header/breadcrumb.vue

<template><el-breadcrumb separator="/"><el-breadcrumb-item v-for="(item,index) in breadcrumbList" :key="index"><span class="no-redirect" v-if="index==breadcrumbList.length-1">{{item.name}}</span><span class="redirect" v-else @click="handleRedirect(item.path)">{{item.name}}</span></el-breadcrumb-item></el-breadcrumb>
</template><script setup>
import {ref, watch} from 'vue'
import { useRoute,useRouter } from 'vue-router'
const route=useRoute();
const router=useRouter();
console.log(route.matched)const breadcrumbList=ref([]);const handleRedirect=(path)=>{router.push(path)
}const initBreadcrumbList=()=>{breadcrumbList.value=route.matched;
}watch(route,()=>{initBreadcrumbList();
},{deep:true,immediate:true})</script><style lang="scss" scoped>
.no-redirect{cursor:text;
}
.redirect{color:#666;font-weight:600;cursor:pointer;&:hover{color:#304156}
}
</style>

layout index.vue修改：

<template><div class="app-wrapper"><el-container><el-aside width="200px" class="sidebar-container"><Menu/></el-aside><el-container><el-header><div class="navbar"><Breadcrumb/></div></el-header><el-main><router-view/></el-main></el-container></el-container></div>
</template><script setup>
import Menu from '@/views/layout/menu'
import Breadcrumb from '@/views/layout/header/breadcrumb'
</script><style lang="scss" scoped>.app-wrapper {position: relative;width: 100%;height: 100%;
}.navbar {width: 100%;height: 60px;overflow: hidden;background-color: #fff;box-shadow: 0 1px 4px rgba(0, 21, 41, 0.08);padding: 0 16px;display: flex;align-items: center;box-sizing: border-box;position: relative;
}:deep(.el-header){padding: 0px;
}.sidebar-container {background-color: #2d3a4b;height: 100%;
}:deep(.el-container){height: 100%;
}</style>

views/home/index.vue

<template>后台管理首页
</template><script>
export default {name: "index"
}
</script><style scoped></style>

views/bigType/index

<template>
商品大类
</template><script>
export default {name: "index"
}
</script><style scoped></style>