1. 岭回归和Lasso回归的基本原理
1.1 岭回归:
岭回归(Ridge Regression) 是一种用于共线性数据分析的技术。共线性指的是自变量之间存在高度相关关系。岭回归通过在损失函数中添加一个L2正则项( λ ∑ j = 1 n β j 2 \lambda \sum_{j=1}^{n} \beta_j^2 λ∑j=1nβj2)来减小回归系数的大小,从而控制模型的复杂度和防止过拟合。这里的 λ \lambda λ是正则化强度参数。
1.2 Lasso回归:
Lasso回归(Least Absolute Shrinkage and Selection Operator) 通过在损失函数中添加一个L1正则项( λ ∑ j = 1 n ∣ β j ∣ \lambda \sum_{j=1}^{n} |\beta_j| λ∑j=1n∣βj∣)来进行变量选择和复杂度调控。Lasso回归倾向于产生一些精确为零的系数,从而实现了变量的自动选择,有助于提高模型的解释能力。
2. MATLAB中岭回归和Lasso回归的实现
岭回归实现:
MATLAB使用ridge函数实现岭回归。此函数要求自变量矩阵进行中心化和标准化。
Lasso回归实现:
MATLAB通过lasso函数实现Lasso回归,提供了一个方便的接口来执行变量选择和正则化。
3. 实例分析
假设我们有一组数据,包括多个自变量(X1, X2, …, Xn)和一个因变量(Y),我们将使用岭回归和Lasso回归来建模,并比较结果。
3.1 岭回归分析代码
clc,clear
% 设置随机数种子以保证结果的可复现性
rng(0);% 生成模拟数据
n_samples = 100;
n_features = 5;
X = randn(n_samples, n_features);
true_coeffs = [3.5; -2; 0; 4; -1]; % 真实系数
Y = X * true_coeffs + randn(n_samples, 1) * 1.5; % 添加噪声% 继续进行岭回归分析
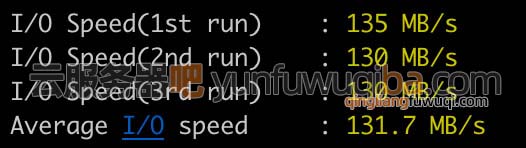
lambda = 0.1:0.1:10; % 设置一系列的正则化强度参数
ridgeCoeffs = ridge(Y, X, lambda, 0)% 绘制岭回归系数随lambda变化的图
figure;
plot(lambda, ridgeCoeffs(2:end, :)); % 从第二行开始绘制,因为ridge函数的第一行是截距项
xlabel('Lambda');
ylabel('Coefficients');
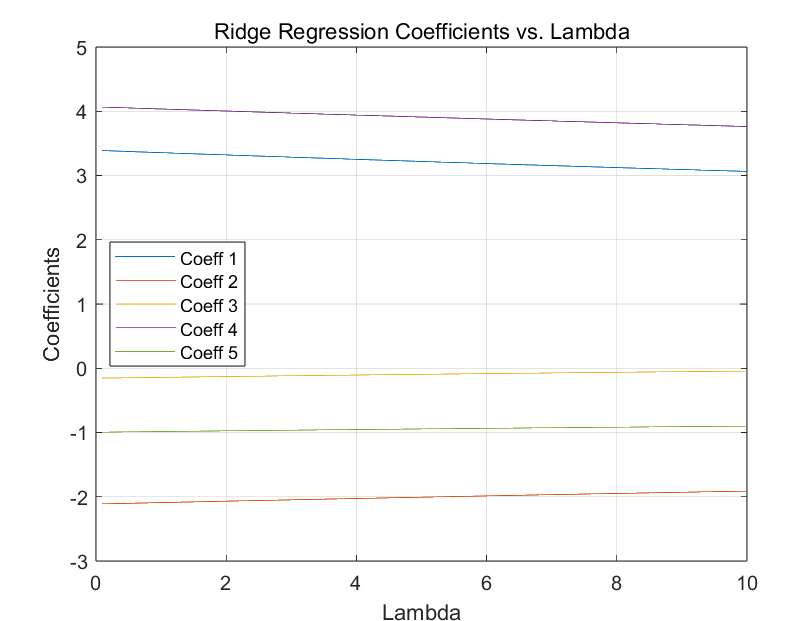
title('Ridge Regression Coefficients vs. Lambda');
legend(arrayfun(@(n) sprintf('Coeff %d', n), 1:n_features, 'UniformOutput', false), 'Location', 'Best');
grid on;
3.2 Lasso回归分析代码
clc,clear
% 设置随机数种子以保证结果的可复现性
rng(0);% 生成模拟数据
n_samples = 100;
n_features = 5;
X = randn(n_samples, n_features);
true_coeffs = [3.5; -2; 0; 4; -1]; % 真实系数
Y = X * true_coeffs + randn(n_samples, 1) * 1.5; % 添加噪声% Lasso回归分析
[B, FitInfo] = lasso(X, Y, 'CV', 10); % 进行Lasso回归,并使用10折交叉验证% 选取最佳Lambda值对应的系数
idxLambda1SE = FitInfo.Index1SE;
coef = B(:, idxLambda1SE);%最佳Lambda值对应的系数
coef0 = FitInfo.Intercept(idxLambda1SE);%最佳Lambda值对应的截距项
disp('最佳Lambda值对应的系数:')
disp(coef)
disp('最佳Lambda值对应的截距项:')
disp(coef0)
lassoPlot(B, FitInfo, 'PlotType', 'Lambda', 'XScale', 'log');%绘制系数路径
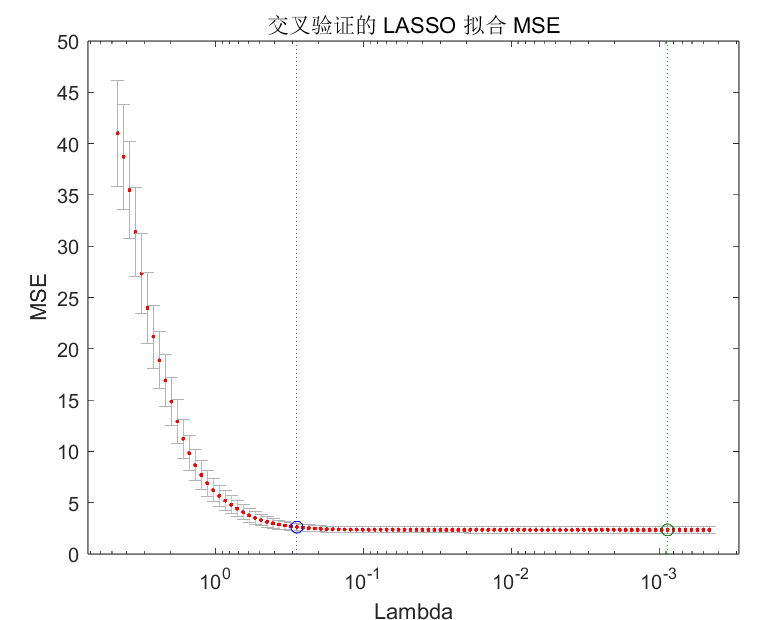
lassoPlot(B, FitInfo, 'PlotType', 'CV');%绘制交叉验证误差
4. 求解结果
4.1 岭回归:
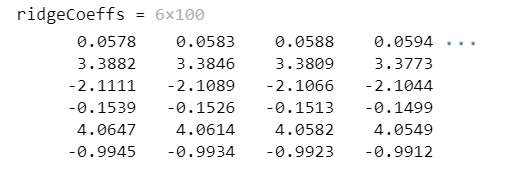
绘制每个系数随 λ \lambda λ变化的图:
4.2 Lasso回归:


5. 结果解释和应用
- 岭回归:通过调整 λ \lambda λ值,可以观察不同正则化强度对模型系数的影响。较大的 λ \lambda λ值会使系数更小,有助于减少过拟合。
- Lasso回归:Lasso回归结果可以帮助我们识别哪些变量对预测最重要,因为不重要的变量系数会被压缩到0。
6. 结论
岭回归和Lasso回归都是处理高维数据和防止过拟合的有效方法。岭回归通过L2正则化减小系数值,而Lasso回归既可以通过L1正则化减小系数值,又可以实现变量选择。在实际应用中,选择哪一种方法取决于具体问题和数据集的特点。