来源

题目

Tokitsukaze 有一个长度为 n 的序列 a1,a2,…,an和一个整数 k。

她想知道有多少种序列 b1,b2,…,bm满足：
 

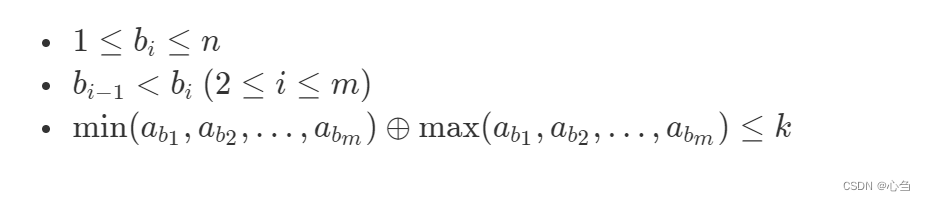
其中 ⊕\oplus⊕ 为按位异或，具体参见 百度百科：异或 

答案可能很大，请输出  mod1e9+7 后的结果。

输入描述:

第一行包含一个整数 T(1≤T≤2e5)，表示 T 组测试数据。对于每组测试数据：第一行包含两个整数 n, k (1≤n≤2⋅e5; 0≤k≤1e9)。第二行包含 nnn 个整数 a1,a2,…,an (0≤ai≤1e9)。

输出描述:

对于每组测试数据，输出一个整数，表示答案   mod1e9+7  后的结果。

输入

3
3 2
1 3 2
5 3
1 3 5 2 4
5 0
0 0 0 0 0

输出

6
10
31

思路

       容易知道 b1,…,bm 实际上是 a 的一个子序列，并且由于我们只关注子序列中的最大值和最小值，因此可以先对 a 从小到大排序，再选择子序列。接着对子序列中的最大值进行分类，可以分成 n 类。即从左到右依次枚举 ai 作为子序列中的最大值，那么最小值就会在 aj, j∈[0,i] 中选。当满足 ai⊕aj≤k，那么以 ai 为最大值，aj 为最小值的子序列的数量就是 2的max{0,i−j−1}次方，特别的当 i=j 时答案为 1。

       暴力的做法就是逐个枚举 aj 判断是否满足条件，时间复杂度是 O() 的。由于涉及到异或运算所以尝试能不能用 trie 来维护 aj 的信息。如果 aj 满足条件，那么对答案的贡献是 ，也就是 ，因此在把 aj 按位插入 trie 中时，同时在对应节点加上。

       枚举到 ai 时，此时已经往 trie 中插入了 a0∼ai−1，枚举 ai 的每一位，用 xi 和 ki 分别表示 ai 和 k 在二进制下第 i 位上的值，s表示累加和。

        1.当xi=1，ki=1时，显然另一数aj这一位是1的情况都是可以的，因为 1⊕1=0<1，所以s加上这一位为1的节点的值了，下一步走0节点。

        2.当xi=0，ki=1时，同理s加上0节点的值，下一步走1节点.

        3.当xi=1，ki=0时，0节点必然不成立，因为 1⊕0=1>0，下一步走1节点。

        4.当xi=0，ki=0时，同理，1节点必然不成立，下一步走0节点。

最后以 ai 为最大值的子序列的数量就是。

代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
//#define double long double
typedef long long ll;
const int N = 2e5+100;
const int mod = 1e9+7;
const int INF = 0x3f3f3f3f3f3f3f;
//ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);int a[N];
int to[N * 35][2];
int val[N * 35];
int tot = 0;void insert(int x,int c) {int p = 0;for (int i = 30; i >= 0; i--) {int v = (x >> i & 1);if (!to[p][v]) {to[p][v] = ++tot;}val[to[p][v]] = (val[to[p][v]] + c) % mod;p = to[p][v];}
}int sum(int x,int k) {int p = 0, res = 0;for (int i = 30; i >= 0; i--) {int vx = (x >> i & 1), vk = (k >> i & 1);if (vk == 1 && vx == 1) {res = (res + val[to[p][1]]) % mod;p = to[p][0];} else if (vk == 1 && vx == 0) {res = (res + val[to[p][0]]) % mod;p = to[p][1];} else {p = to[p][vx];}if (!p) break;if (!i) res = (res + val[p]) % mod;}return res;
}int ksm(int x,int n) {int res = 1;while (n) {if (n & 1) res = res * x % mod;x = x * x % mod;n >>= 1;}return res;
}void solve() {int n,k;cin >> n >> k;for(int i=0;i<n;i++)cin>>a[i];sort(a,a+n);tot = 0;for (int i = 0; i <= n * 32; i++) {val[i] = 0;to[i][0] = to[i][1] = 0;}int ans = 0;for (int i = 1; i <= n; i++) {ans = (ans + 1 + ksm(2,i - 1) * sum(a[i - 1],k) % mod) % mod;insert(a[i - 1],ksm(ksm(2,i),mod - 2));}cout << ans << '\n';
}signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t=1;cin>>t;while(t--)solve();return 0;
}