剑指offer——旋转数组的最小数字-编程知识

1. 题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3.4,5,1.2}为{1.2,3,4,5}的一个旋转，该数组的最小值为 1。

2. 分析思路

这道题最直观的解法并不难，从头到尾遍历数组一次，我们就能找出最小的元素。
这种思路的时间复杂度显然是O(n)。但是这个思路没有利用输入的旋转数组的特性，肯定达不到面试官的要求。
我们注意到旋转之后的数组实际上可以划分为两个排序的子数组，而且前面的子数组的元素都大于或者等于后面子数组的元素。
我们还注意到最小的元素刚好是这两个子数组的分界线。
在排序的数组中我们可以用二分查找法实现 O(logn)的查找。
本题给出的数组在一定程度上是排序的，因此我们可以试着用二分查找法的思路来寻找这个最小的元素。
和二分查找法一样，我们用两个指针分别指向数组的第一个元素和最后一个元素。
按照题目中旋转的规则，第一个元素应该是大于或者等于最后一个元素的(这其实不完全对，还有特例，后面再加以讨论)。

接着我们可以找到数组中间的元素。
如果该中间元素位于前面的递增子数组，那么它应该大于或者等于第一个指针指向的元素。
此时数组中最小的元素应该位于该中间元素的后面。
我们可以把第一个指针指向该中间元素，这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。
同样，如果中间元素位于后面的递增子数组，那么它应该小于或者等于第二个指针指向的元素。
此时该数组中最小的元素应该位于该中间元素的前面。
我们可以把第二个指针指向该中间元素，这样也可以缩小寻找的范围。
移动之后的第二个指针仍然位于后面的递增子数组之中。
不管是移动第一个指针还是第二个指针，查找范围都会缩小到原来的一半。接下来我们再用更新之后的两个指针，重复做新一轮的查找
按照上述的思路，第一个指针总是指向前面递增数组的元素，而第一个指针总是指向后面递增数组的元素。
最终第一个指针将指向前面子数组的最后一个元素，而第二个指针会指向后面子数组的第一个元素。
也就是它们最终会指向两个相邻的元素，而第二个指针指向的刚好是最小的元素。这就是循环结束的条件。

2.1 示例分析

以前面的数组{3.4,5.1.2}为例，我们先把第一个指针指向第0个元素，把第二个指针指向第4个元素(如图2.10(a)所示)。
位于两个指针中间(在数组中的下标是2)的数字是5，它大于第一个指针指向的数字。
因此中间数字5一定位于第一个递增子数组中，并且最小的数字一定位于它的后面。
因此我们可以移动第一个指针让它指向数组的中间(图2.10(b)所示)。

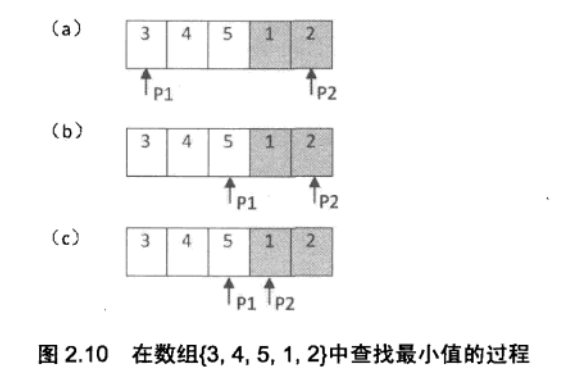
在这里插入图片描述

注:旋转数组中包含两个递增排序的子数组，有阴影背景的是第二个子数组。(a)把P1指向数组的第一个数字，P2指向数组的最后一个数字。由于P1和P2中间的数字5大于P1指向的数字，中间的数字在第一个子数组中。下一步把P1指向中间的数字。(b)P1和P2中间的数字1小于 P2指向的数字，中间的数字在第二个子数组中。下一步把P2指向中间的数字。©P1和P2指向两个相邻的数字，则P2指向的是数组中的最小数字。

此时两个指针的距离是1,表明第一个指针已经指向了第一个递增子数组的末尾，而第二个指针指向第二个递增子数组的开头。
第二个子数组的第一个数字就是最小的数字，因此第二个指针指向的数字就是我们查找的结果。
基于这个思路我们可以写出如下代码：

#define ROW 5
#include <stdio.h>int search(int arr[ROW], int len)
{if (arr == NULL || len <= 0){return;}int p1 = 0;int p2 = len - 1;int mid = p1;while (arr[p1] >= arr[p2]){if (p2 - p1 == 1){mid = p2;break;}mid = (p1 + p2) / 2;if (arr[mid] >= arr[p1]){p1 = mid;}else if (arr[mid] <= arr[p2]){p2 = mid;}}return arr[mid];}int main()
{int arr[ROW] = { 3, 4, 5, 1, 2 };printf("%d\n", search(arr, ROW));return 0;
}

运行结果为：

在这里插入图片描述

前面我们提到在旋转数组中，由于是把递增排序数组前面的若干个数字搬到数组的后面，因此第一个数字总是大于或者等于最后一个数字。
但按照定义还有一个特例:如果把排序数组的前面的0个元素搬到最后面，即排序数组本身，这仍然是数组的一个旋转，我们的代码需要支持这种情况。
此时，数组中的第一个数字就是最小的数字，可以直接返回。
这就是在上面的代码中，把 indexMid 初始化为 index1的原因。一旦发现数组中第一个数字小于最后一个数字，表明该数组是排序的，就可以直接返回第一个数字了。

3. 更完美的做法

上述代码是否就完美了呢?面试官会告诉我们其实不然。
他将提示我们再仔细分析下标为indexl和 index2(indexl和index2 分别和图中 P1和P2 相对应)的两个数相同的情况。
在前面的代码中，当这两个数相同，并且它们中间的数字(即 indexMid 指向的数字)也相同时，我们把 indexMid赋值给了 index1，也就是认为此时最小的数字位于中间数字的后面。
是不是一定这样?

在这里插入图片描述

注:在这两个数组中，第一个数字、最后一个数字和中间数字都是1,我们无法确定中间的数字 1 属于第一个递增子数组还是属于第二个递增子数组。第二个子数组用灰色背景表示。

在这两种情况中，第一个指针和第二个指针指向的数字都是1，并且两个指针中间的数字也是1,这3个数字相同。
在第一种情况中，中间数字(下标为 2)位于后面的子数组;在第二种情况中，中间数字(下标为2)位于
前面的子数组中。因此，当两个指针指向的数字及它们中间的数字三者相同的时候，我们无法判断中间的数字是位于前面的子数组中还是后面的子数组中，也就无法移动两个指针来缩小查找的范围。
此时，我们不得不采用顺序查找的方法。
把问题分析清楚了之后，我们就可以把代码修改为：

#define ROW 5
#include <stdio.h>int search_(int arr[ROW], int p1, int p2)
{int min = arr[p1];for (int i = p1 + 1; i <= p2; i++){if (arr[i] < min){min = arr[i];}}return min;
}int search(int arr[ROW], int len)
{if (arr == NULL || len <= 0){return;}int p1 = 0;int p2 = len - 1;int mid = p1;while (arr[p1] >= arr[p2]){if (p2 - p1 == 1){mid = p2;break;}mid = (p1 + p2) / 2;if (arr[p1] == arr[mid] && arr[mid] == arr[p2]){return search_(arr, p1, p2);}if (arr[mid] >= arr[p1]){p1 = mid;}else if (arr[mid] <= arr[p2]){p2 = mid;}}return arr[mid];
}int main()
{int arr[ROW] = { 1, 0, 1, 1, 1 };printf("%d\n", search(arr, ROW));return 0;
}