一、平衡二叉树

平衡二叉树：是一棵空树或它的左右两个子树的高度差的绝对值不超过 1， 并且左右两个子树都是一棵平衡二叉树。

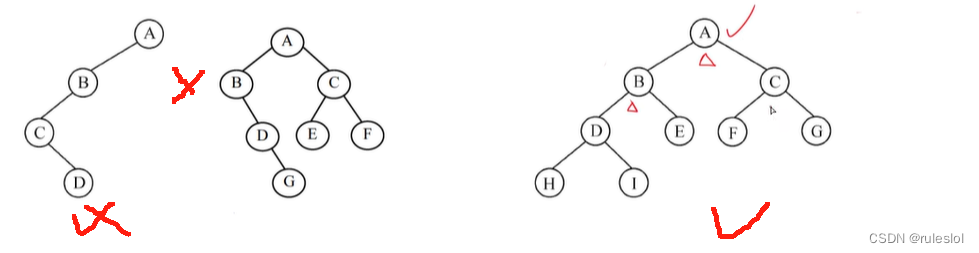
注意：

完全二叉树 = 平衡二叉树！！！

二、二叉排序树（二叉查找树、二叉搜索树）

2-1、二叉排序树的定义

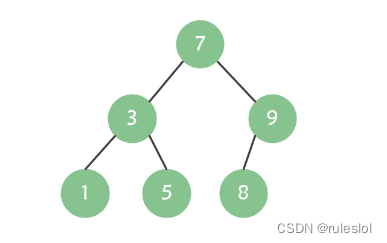
对于二叉排序树的任何一个非叶子节点，要求左子节点的值比当前节点的值小，右子节点的值比当前节点的值大（如果有相同的值，则该节点放在左子节点或右子节点都可）。

左子树节点的值 < 根节点的值 < 右子树结点的值

二叉排序树的特点：

中序遍历，得到的序列是有序序列。

示例：

2-2、二叉排序树的构造

出题方式：给一组关键字序列，用这组关键字序列构造二叉排序树。

构造方式：第一个关键字是根节点，然后依次遍历后面的关键字，比根节点小的，就往左挂，比根节点大的就往右挂。

示例：23 31 17 19 11 27 13 90 61

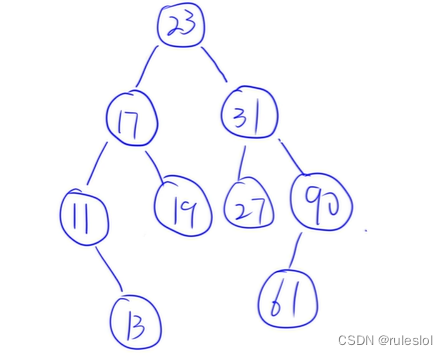
不同的关键字序列可以构造相同的二叉排序树。

2-3、真题

真题1：

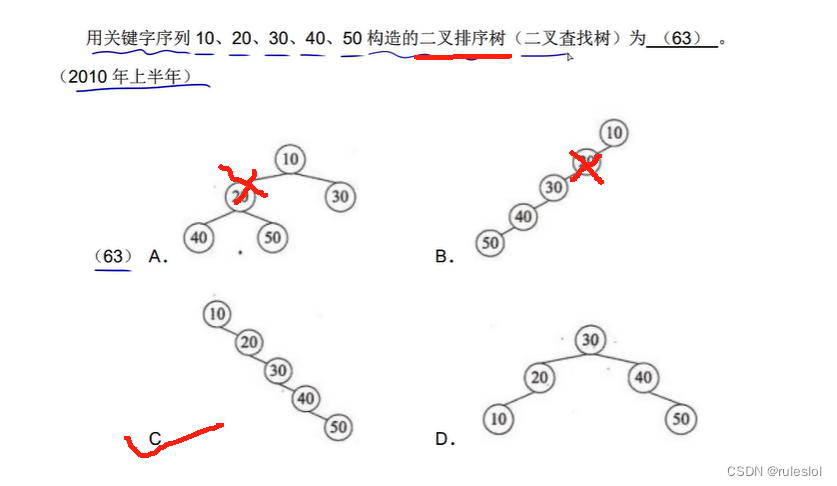
真题2：

真题3：

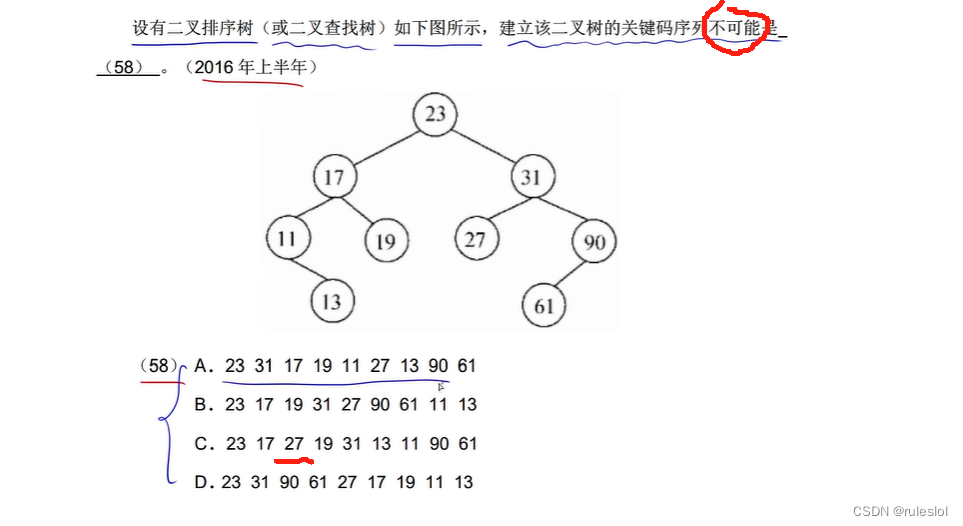
真题4：

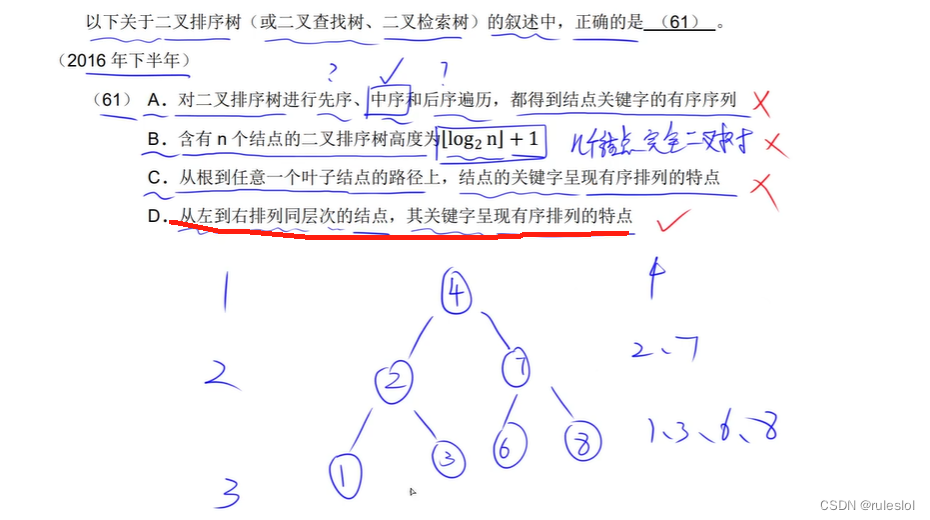
真题5：

三、最优二叉树（哈夫曼树）

3-1、哈夫曼树的定义

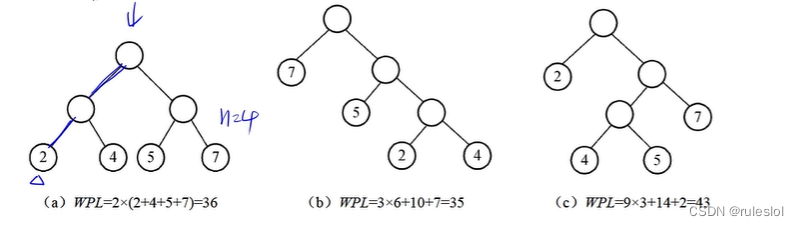
带权路径长度最短的树。

结点的带权路径长度：该节点到树根之间的路径长度 * 该节点的权值

树的带权路径长度 = 树中所有叶子结点的带权路径长度只和。

示例：

3-2、构造哈夫曼树

给定n个权值{w1, w2, w3, ......, w4, w5}，构成n棵二叉树的集合F = {T1, T2, T3, ......, Tn}；

1、选择根结点权值最小的两棵二叉树，并以它们为左右子树构造一棵新的二叉树，新二叉树根结点的权值为其左右子树根结点权值之和。 

2、从F中删除选择的两棵二叉树，并将新二叉树放到集合F中，继续步骤1。

以选中的两棵子树构成新的二叉树，哪个作为左子树，哪个作为右子树，并没有明确。所以，最优二叉树不唯一，但其 WPL的值是唯一确定的。

构造哈夫曼树的原则：（能够减小二叉树的带权路径长度）

权值大的叶子结点离根结点近；

权值小的叶子结点离根结点远

3-3、哈夫曼树的性质

1、只有度为0、2，没有度为1的节点；

2、用n个节点构造哈夫曼树，这n个节点都会变成叶子结点；

3、哈夫曼树的总节点个数：2n-1；

3-4、哈夫曼树的构造规律

• 从前往后，找两个权值最小的；
• 构造的时候，左小右大；
• 新的根节点，加入到结尾
• 权值相同，从前往后取结点
• 用时再调

目的：正确求出哈夫曼编码

3-5、哈夫曼编码

英文字符集中的26个字符可用？位二进制位表示？

2^5 = 32 > 26

即可用5位二进制位表示。

规定哈夫曼树中的左分支为0，右分支为1，从根节点到叶子结点所经过的分支对应的0和1组成的序列便为该节点对应字符的编码。

示例：

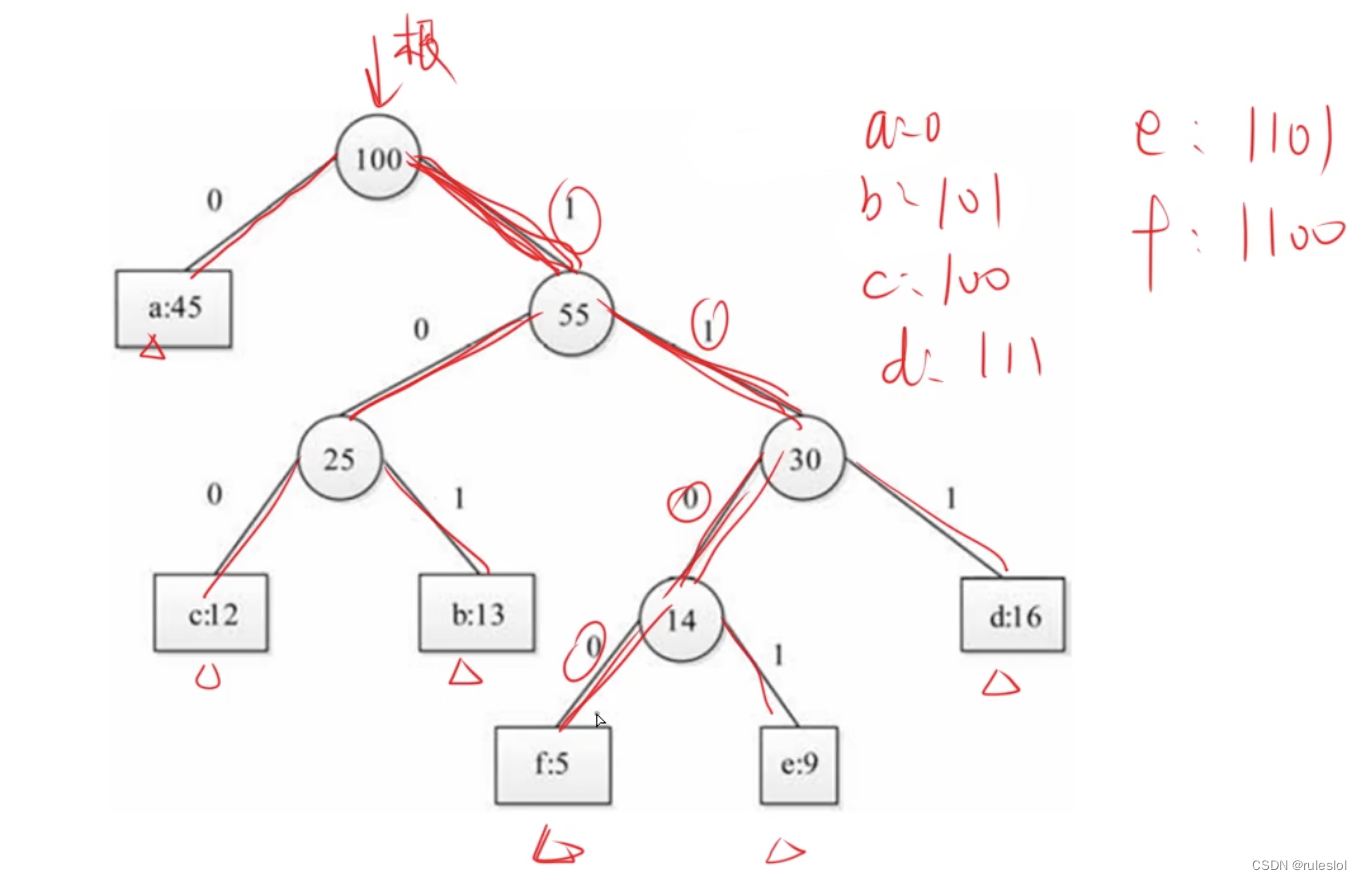
哈夫曼编码的特点：

        在一组字符的哈夫曼编码中，不可能出现一个字符的哈夫曼编码是另一个字符哈夫曼编码的前缀。 

3-6、哈夫曼编码压缩比

示例：

因为有5中不同的字符，2^3 = 8 >= 5，所以，等长编码最少有3位。

以频率作为权重，构造哈夫曼树：

因此，各字符的编码为：

按照出现频率计算加权平均长度：字符位数 * 出现频率

a的位数 * 40% + b的位数 * 10% + c的位数 * 20% + d的位数 * 16% + e的位数 * 14%

= 1 * 40% + 3 * 10% + 3 * 20% + 3 * 16% + 3 * 14%

= 2.2位 

计算压缩比

未压缩长度为 3 ，压缩后平均长度为 2.2

(3 - 2.2)/3 = 27%

3-7、真题

真题1：

n0 = n2 + 1 

真题2：

真题3：

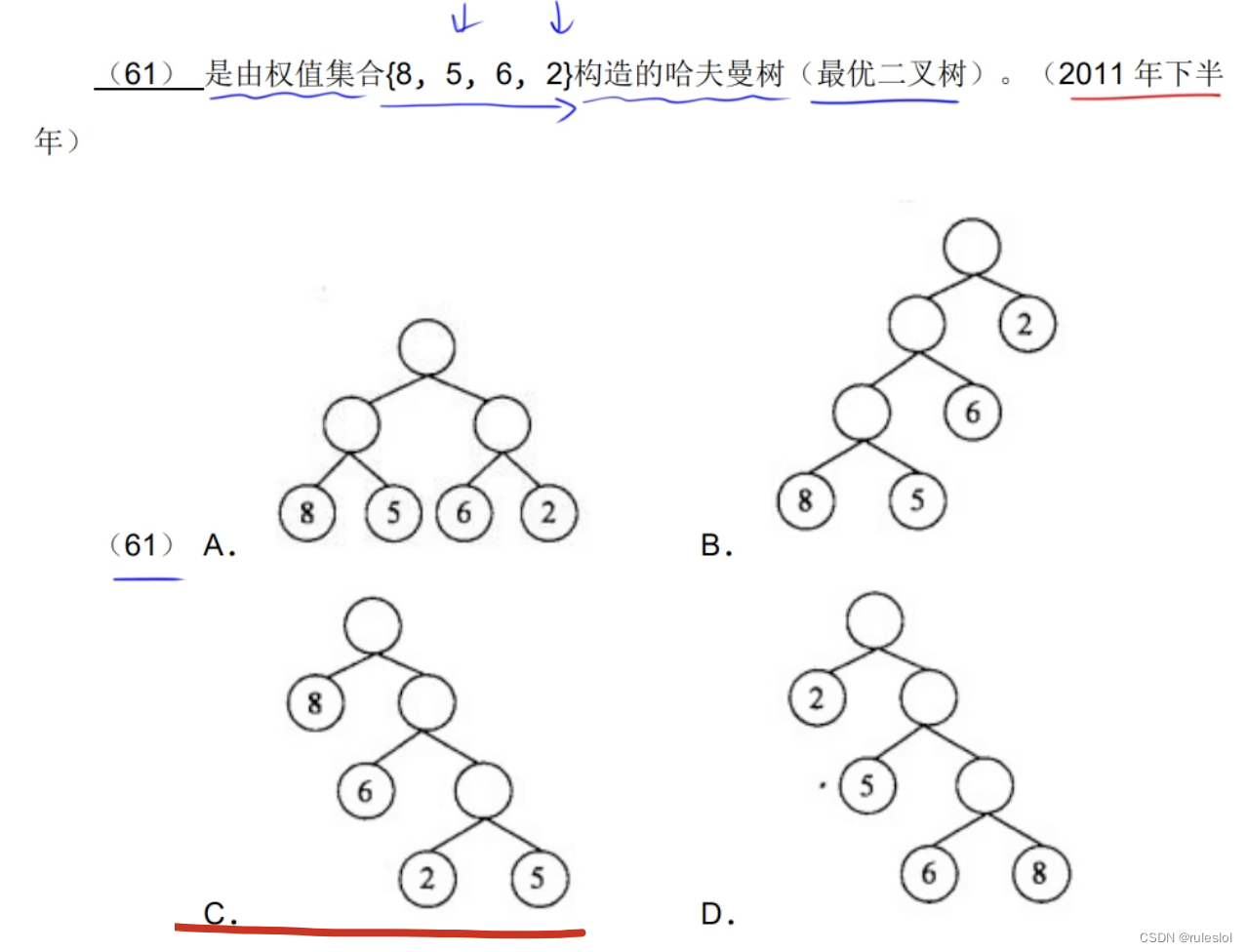
真题4：

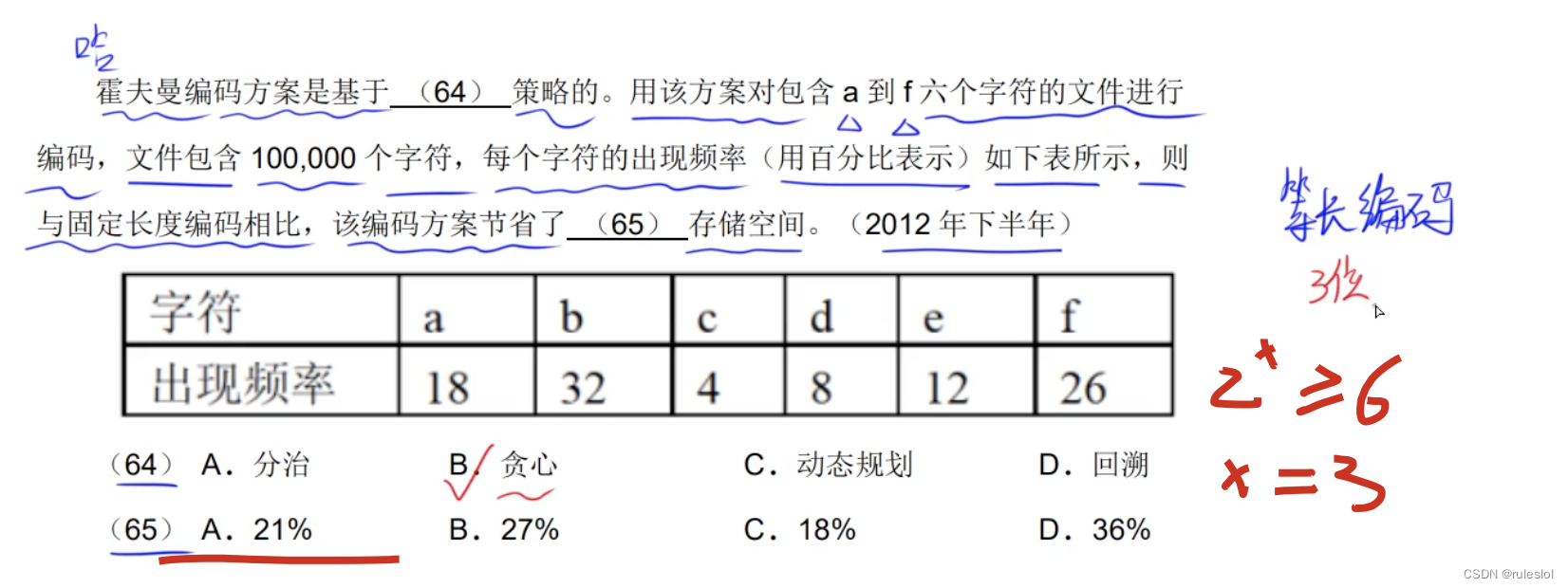
真题5：

真题6：

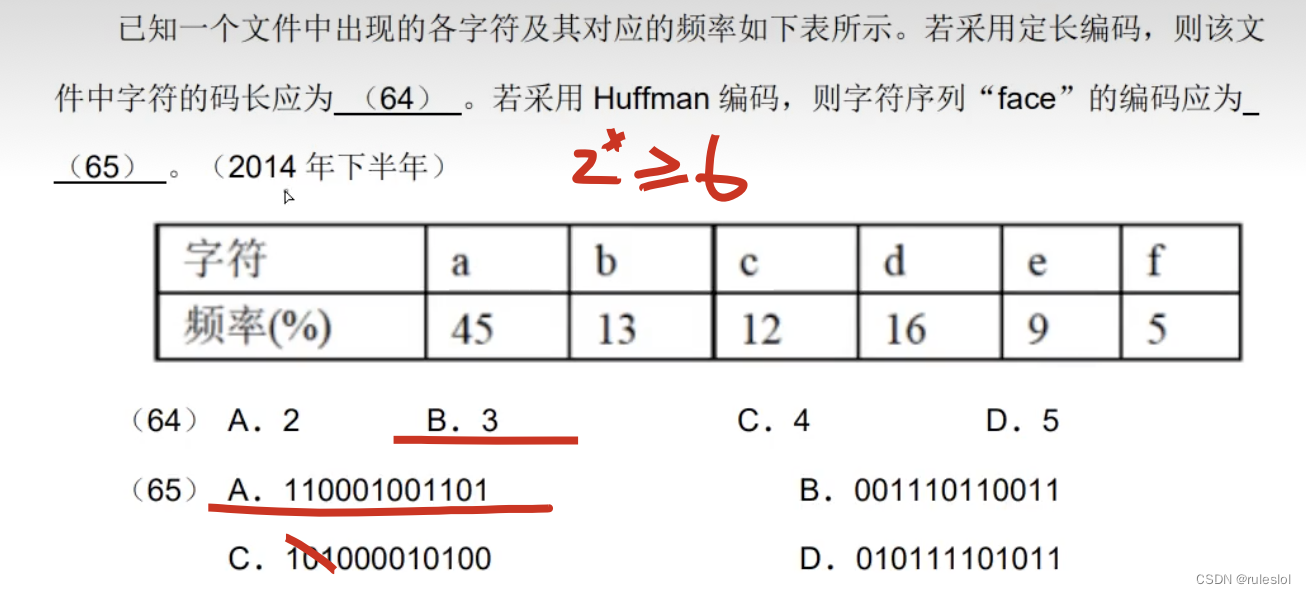
真题7：

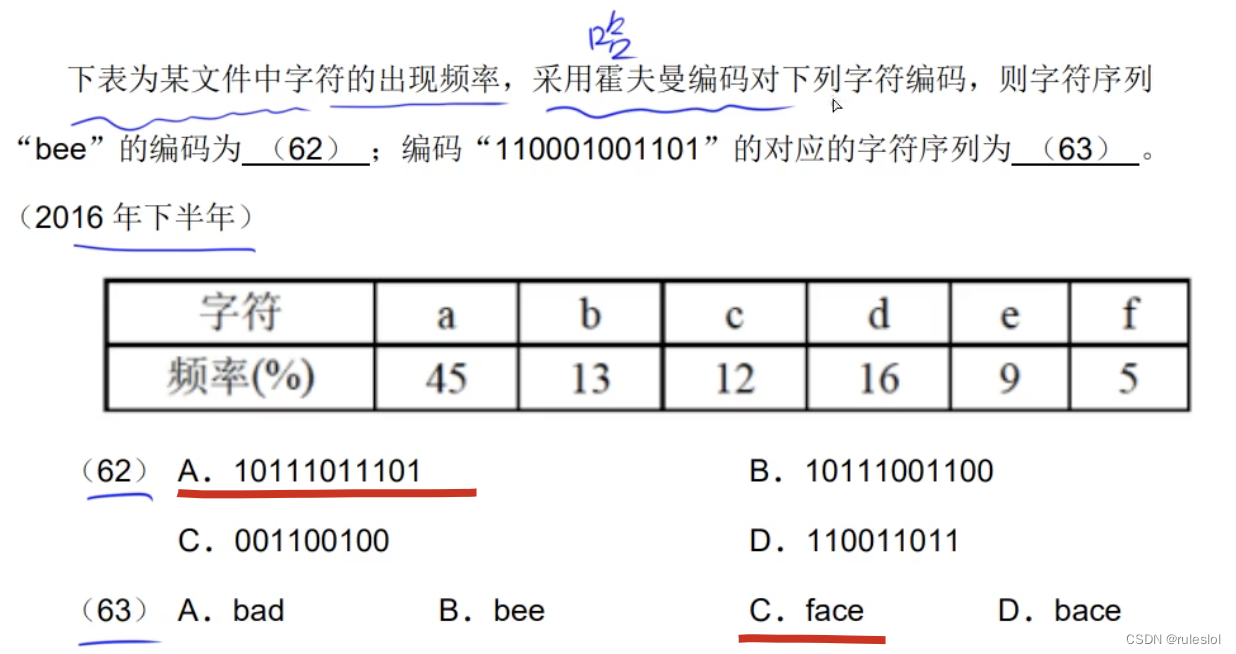
真题8：

真题9：

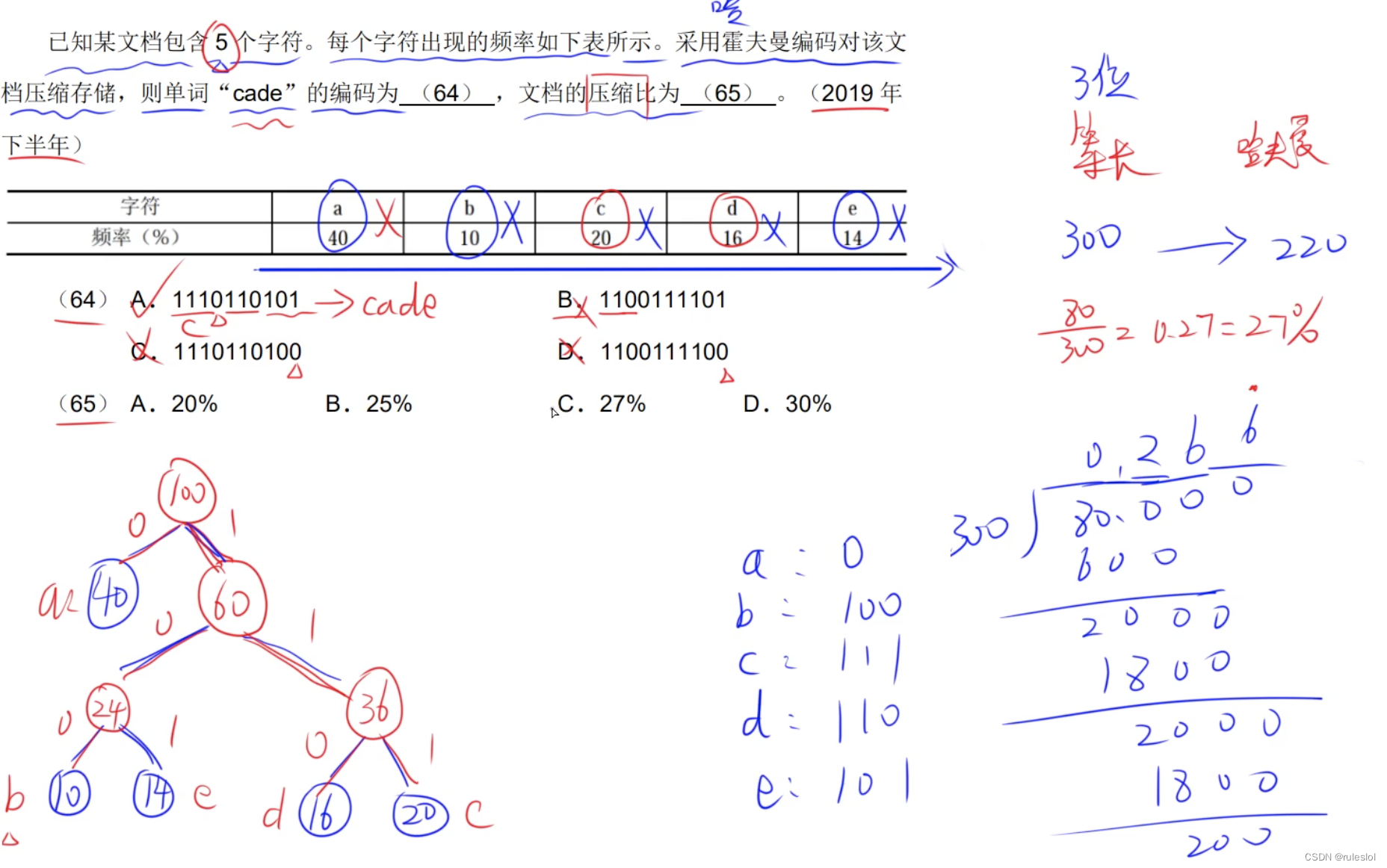
真题10：

真题11：

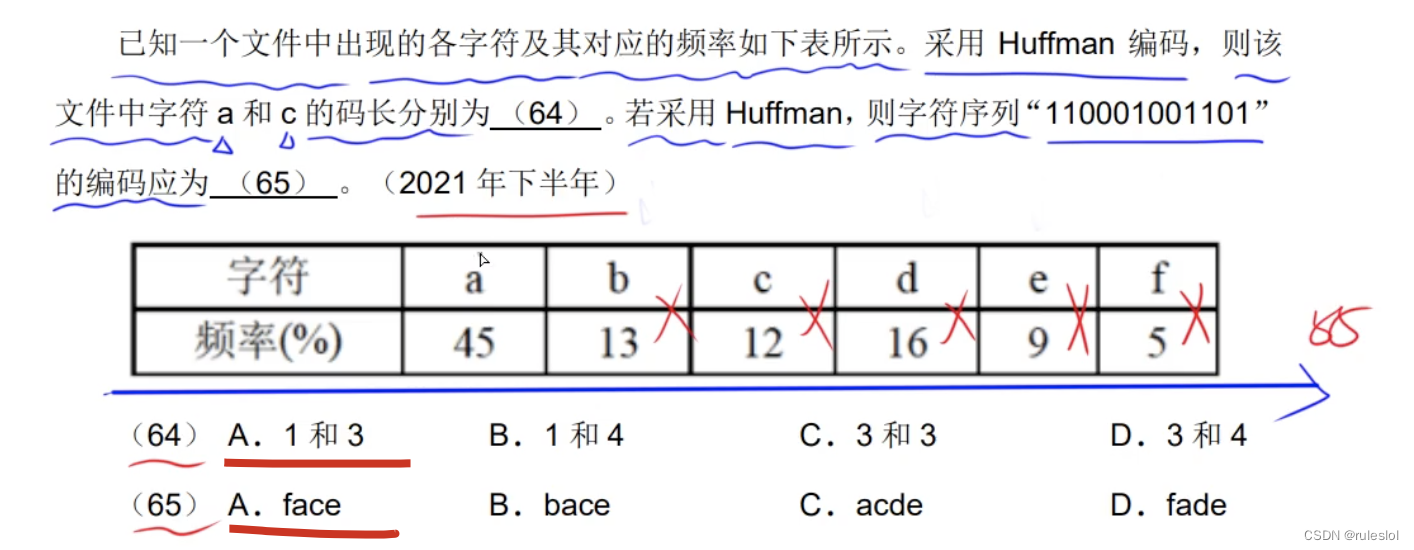
四、线索二叉树

每当涉及到求解前驱或者后继就需要将二叉树遍历一次，非常不方便。可以考虑在每个节点中增加两个指针域来存放遍历时得到的前驱和后继信息。但是，增加指针信息会降低存储空间的利用率。

对于一个有n个结点的二叉链表，每个节点都有指向左右孩子的两个指针域，一共有2n个指针域，n个结点的二叉树又有n-1条分支线数，也就是存在2n-(n-1)=n+1个空指针域。因此, 可以用空链域来存放结点的前驱和后继

示例：

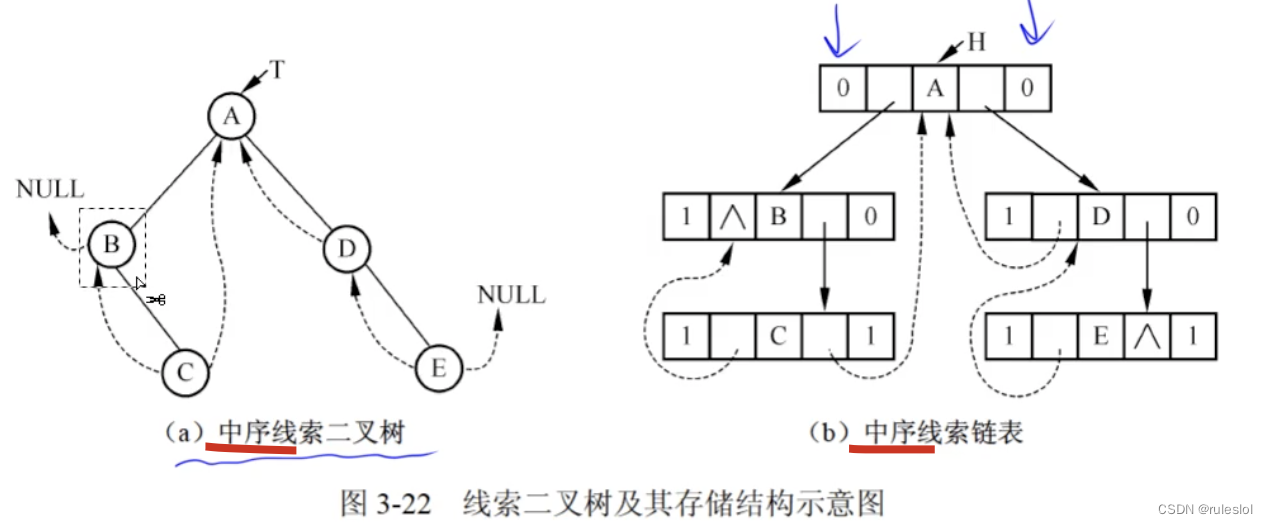
中序遍历：B  C  A  D  E 

五、二叉树类别小结

• 满二叉树
• 完全二叉树
• 平衡二叉树
• 排序二叉树
• 最优二叉树
• 线索二叉树

完全二叉树，是，平衡二叉树

六、真题 

真题1：

 真题2：

真题3：