Day 24

01. 回溯算法理论基础

1.1 什么是回溯法？

👉 递归函数的下面就是回溯的逻辑（有递归就有回溯）

• 递归函数的后面位置其实就是平时提到的 后序位置
• 也就是当前这个节点做完所有的操作返回上一个节点的时候，这时候对这个节点可以通过某些逻辑做回溯的操作

1.2 为什么要使用回溯法？

👉 💡 回溯法是一个纯暴力的搜索方法，并不是一个性能很优的算法

• 当一个题目无法用正常的解法（多层 for 循环嵌套）来求出的时候就需要用到回溯法
• 比如说求 组合问题、切割问题、子集问题、排列问题、棋盘问题

1.3 如何理解回溯法？

👉 将回溯法抽象为一个树形结构

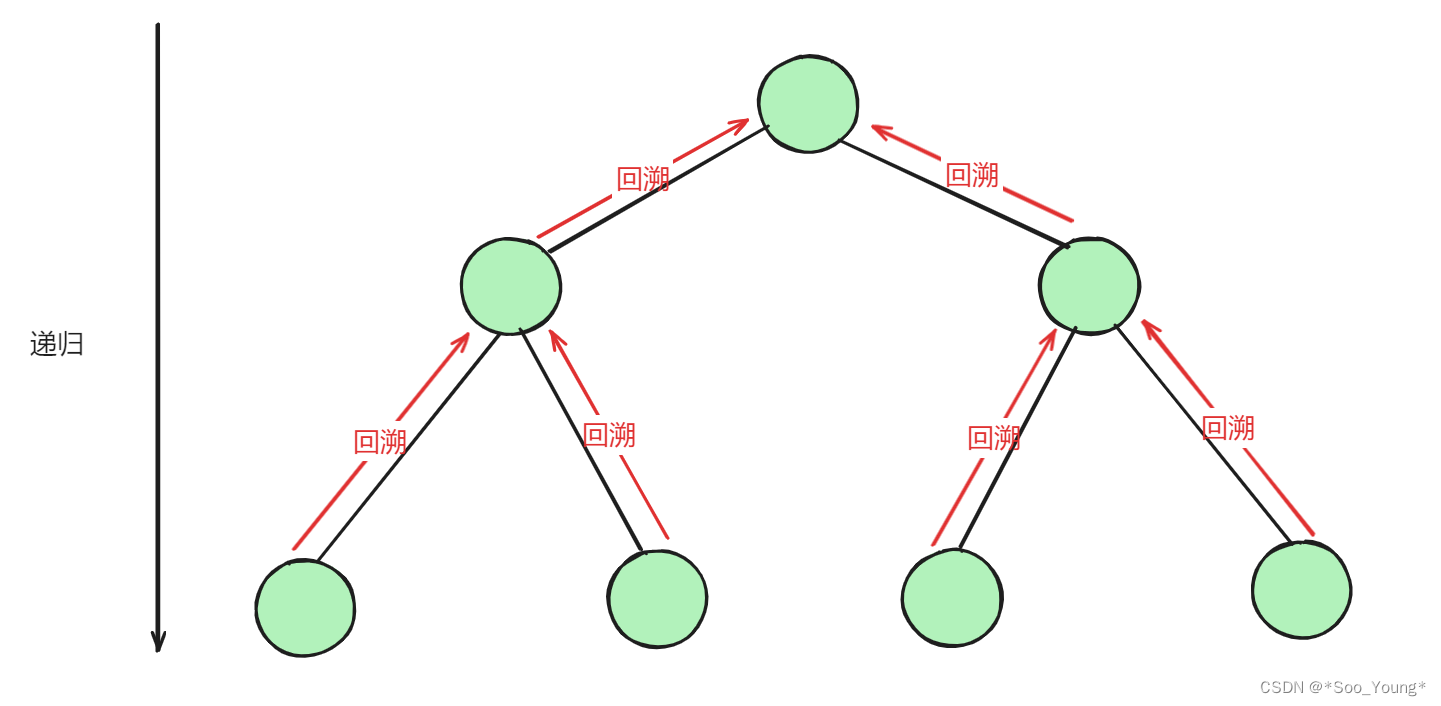
• 递归可以形成一个树形结构，如果一层中只有一个递归就只会形成一个链表结构而不是树形结构，所以一层中是存在多个递归调用的。

• 所以可以总结出回溯法的一个模板

  public void backtracking() {if (...) {return;}for (int i = ...; i < ...; i++) {// 分枝来形成树形结构达到搜索的目的// 回溯算法}
  }
  

02. 组合问题（No. 77）

题目链接

代码随想录题解

2.1 题目

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

2.2 笔记

先来思考这道题为什么需要用回溯算法来解决。

如果要通过 for 循环来解这道题的话会遇到什么困难呢？

如果说固定 k 仅仅限制 n 的话，代码很容易写的出来比如说 k 是 2

List<Integer> path = new ArrayList<>(); // 存储路径值的链表
List<List<Integer>> res = new ArrayList<>(); // 存储结果的链表
for (int i = 1; i <= n; i++) {path.add(i);for (int j = i + 1, i <= n; i++) {path.add(j);res.add(new ArrayList(path));path.remove(path.size() - 1);}path.remove(path.size() - 1);
}

但是如果说 k = 50 或者 k = 100 呢？写一百层 for 循环就会出现很多问题了。

其次不只是书写的问题，通过 for 循环来解题是无法控制 for 循环的层数的

而使用回溯算法可以很容易的解决这个问题

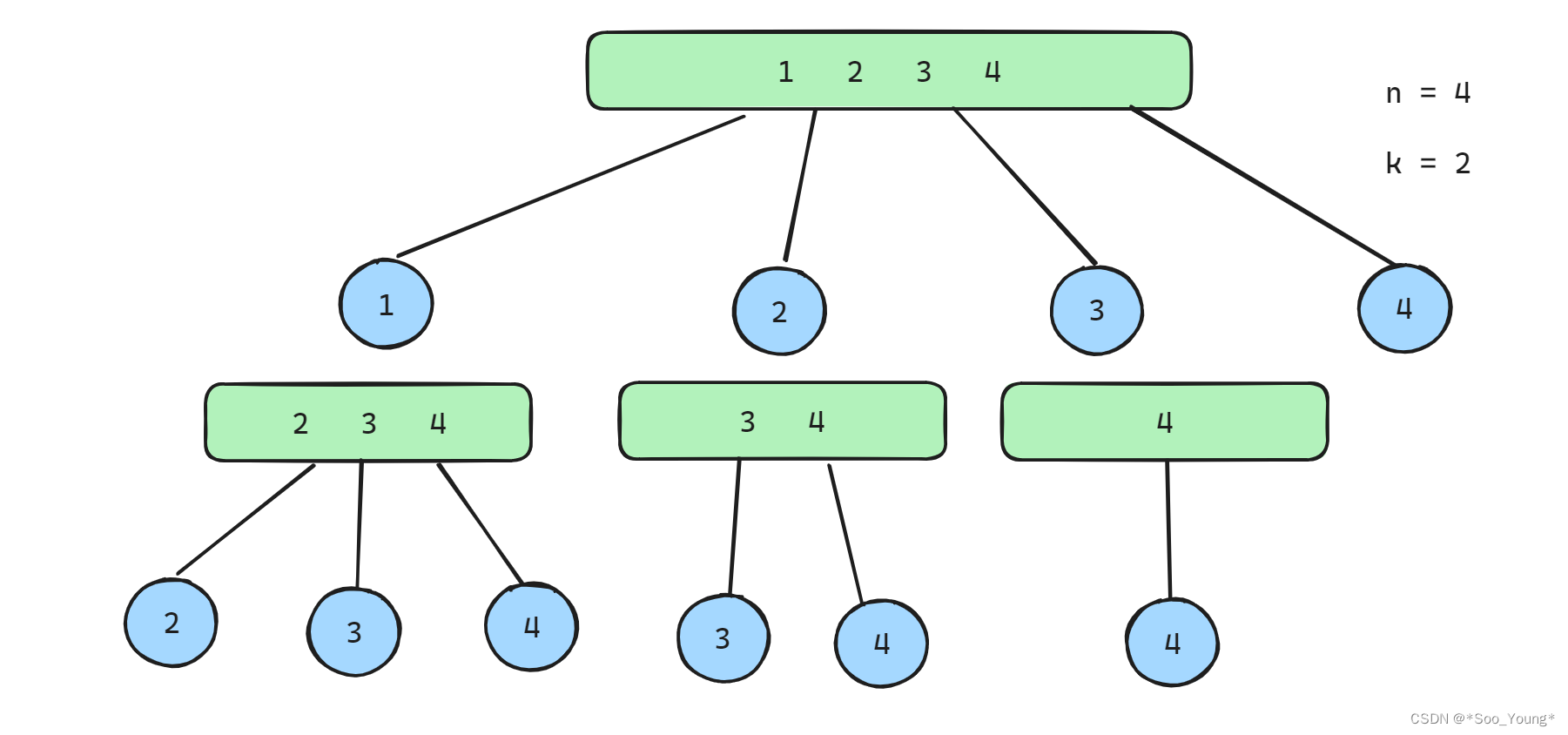
回溯法可以通过递归来控制 for 循环的层数来达到和多层嵌套相同的效果。

这道题的解题思路就是通过一个 List 来收集路径上的节点，当节点的数量等于 k 的时候就收集起来，并且删除掉这个节点来进行后序的遍历。

套用回溯法的模板来解决问题：

public void backtracking() {if (...) {return;}for (int i = ...; i < ...; i++) {// 分枝来形成树形结构达到搜索的目的// 回溯算法}
}

递归结束的条件也就是收集结果的时候，在这道题目中是收集到的节点数目等于 n 的时候，就是 path.size() == n。

然后就是分枝的处理了，先将 1 ~ 4 分成四份然后再从 i 到 n 分成 n - i + 1 份，所以需要一个指针来标识要分成几份 startIndex。

最后就是回溯的代码，和上面说的相同，删除掉这个节点来进行后序的遍历。

2.3 代码

class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n, k, 1);return res;}public void backtracking(int n, int k, int startIndex) {if (path.size() == k) {res.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= n; i++) {path.add(i);backtracking(n, k, i+1);path.remove(path.size() - 1); // 回溯删除节点}}
}