CSP-动态规划-最长公共子序列（LCS）-编程知识

一、动态规划

动态规划（Dynamic Programming，简称DP）主要用于求解可以被分解为相似子问题的复杂问题，特别是在优化问题上表现出色，如最短路径、最大子数组和、编辑距离等。动态规划的核心思想是将原问题分解为较小的子问题，通过解决这些子问题，并将结果存储起来（通常是在一个数组或者哈希表中），以避免重复计算，从而提高效率。

动态规划问题的解决通常遵循以下几个步骤：

暴力穷举所有答案。
画出递归树，尝试编写递归函数求解。
若遍历中存在大量重复计算，使用哈希表缓存数据，之后遍历到相同节点就直接查表。
表示整个计算过程，观察公式求解顺序，改写成更加高效的迭代形式。

二、动态规划的例子

1.斐波那契数列

2.背包问题

3. 最长公共子序列（LCS）

给定一个无序数组nums=[1,5,2,4,3]，找出其中最长的递增的子序列，比如1-2-4，1-2-3。将问题简化，要求算法只返回最长序列的长度（3）

(1) 暴力枚举

把每个子序列都“找个遍”，并且在遍历过程中实时记录当前子序列的长度

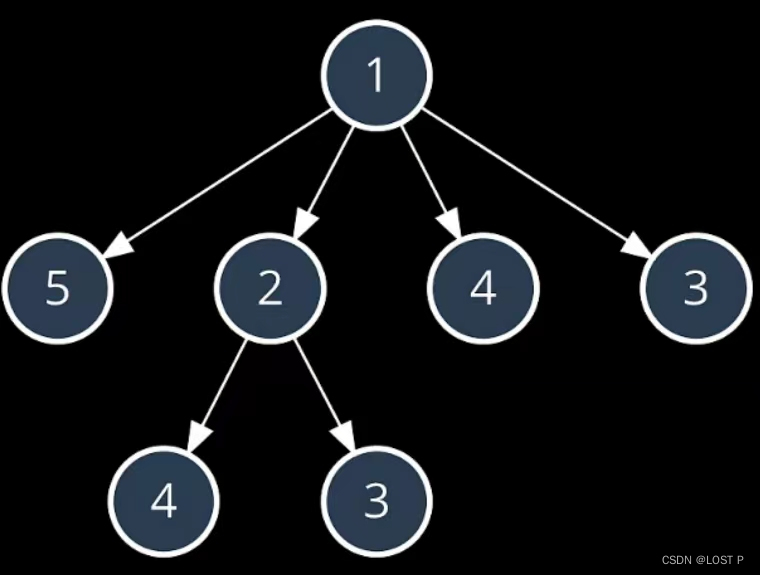
(2) 递归解决方案

递归函数 L：用于计算以特定元素结尾的最长递增子序列的长度；
- 基础情形：如果当前考虑的元素是数组的最后一个元素，那么以它结尾的最长递增子序列的长度为 1，因为它自身就构成了一个长度为 1 的递增子序列。
- 递归步骤：对于非最后一个元素，函数会遍历当前元素之后的所有元素，寻找一个值比当前元素大的元素，这意味着可以形成一个递增的序列。对于每一个这样的元素，函数会递归地计算以那个元素为结尾的最长递增子序列的长度，并将其与当前最大长度比较，更新当前最大长度。这个过程会重复直到数组结束。
- 返回值：函数最终返回以当前元素结尾的最长递增子序列的长度。
函数 lengthOfLIS：作用是找到整个数组的最长递增子序列的长度。
- 遍历给定数组的每个元素，对每个元素调用递归函数 L，计算以该元素为结尾的最长递增子序列的长度。
- 比较并更新 max_len 为当前找到的最长递增子序列的长度。
- 遍历完成后，返回 max_len 作为最终结果。

#include <iostream>
#include <vector>
using namespace std;// 计算以 nums[i] 结尾的最长递增子序列的长度
int L(const vector<int>& nums, int i) {if (i == nums.size() - 1) { // 如果是最后一个元素return 1; // 最长递增子序列长度为1}int max_len = 1; // 初始化最大长度为1for (int j = i + 1; j < nums.size(); ++j) {if (nums[j] > nums[i]) { // 如果找到一个递增的元素// 递归计算以 nums[j] 结尾的最长递增子序列长度，并加1（加上nums[i]）// 然后与当前的最大长度取较大值max_len = max(max_len, L(nums, j) + 1);}}return max_len; // 返回以 nums[i] 结尾的最长递增子序列的长度
}// 计算给定序列的最长递增子序列长度
int lengthOfLIS(const vector<int>& nums) {int max_len = 0; // 初始化全局最大长度为0for (int i = 0; i < nums.size(); ++i) {// 遍历每个元素，计算以每个元素为起点的最长递增子序列的长度// 然后取所有长度中的最大值max_len = max(max_len, L(nums, i));}return max_len; // 返回最长递增子序列的长度
}int main() {vector<int> nums = {1, 5, 2, 4, 3}; cout << lengthOfLIS(nums) << endl; return 0;
}

(3) 递归的问题

直接递归的方法在时间复杂度上是非常高的，因为它会重复计算很多子问题的解。
比如，在遍历子序列1-2-4时就已经计算过“L(4)”，后面遍历1,4时又重复计算了一次。

(4) 递归的优化：动态规划

为了避免递归中出现的重复计算，可以将第一次计算时的结果保存，之后再当遍历到相同的节点我们就不在需要重复计算，直接返回之前的结果即可。
在这个版本中，L 函数中添加了一个 unordered_map （哈希表）类型的备忘录 memo，用于存储已经计算过的子问题的解。在递归的过程中，先检查备忘录是否已经包含了当前子问题的解，如果有则直接返回保存的结果，避免了重复计算。这样能够显著提高程序的性能。

#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;// 使用备忘录的递归方式计算以 nums[i] 结尾的最长递增子序列的长度
int L(const vector<int>& nums, int i, unordered_map<int, int>& memo) {if (i == nums.size() - 1) {return 1;}if (memo.find(i) != memo.end()) {return memo[i]; // 如果已经计算过，直接返回保存的结果}int max_len = 1;for (int j = i + 1; j < nums.size(); ++j) {if (nums[j] > nums[i]) {max_len = max(max_len, L(nums, j, memo) + 1);}}memo[i] = max_len; // 将结果保存到备忘录中return max_len;
}// 计算给定序列的最长递增子序列长度
int lengthOfLIS(const vector<int>& nums) {int max_len = 0;unordered_map<int, int> memo; // 使用unordered_map作为备忘录for (int i = 0; i < nums.size(); ++i) {max_len = max(max_len, L(nums, i, memo));}return max_len;
}int main() {vector<int> nums = {1, 5, 2, 4, 3};cout << lengthOfLIS(nums) << endl;return 0;
}

(5) 递归转非递归

从后往前依次计算，即可推算出所有答案（数学归纳）
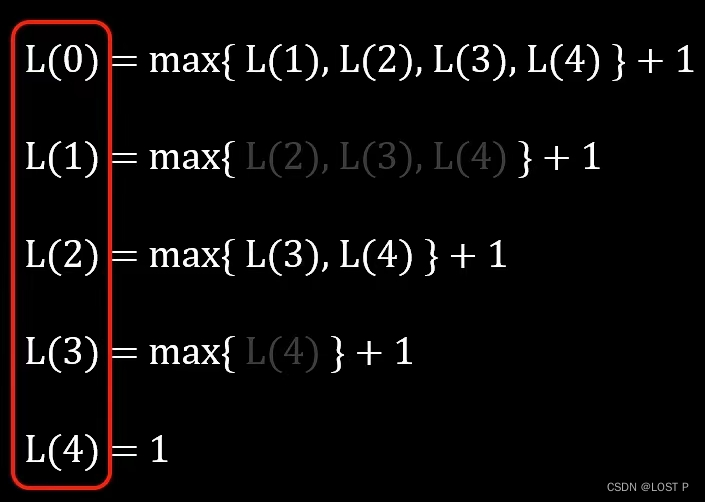
dp 数组：用于存储以每个元素结尾的最长递增子序列的长度。
双重循环：外层循环遍历每个元素，内层循环遍历当前元素之前的元素，更新以当前元素结尾的最长递增子序列的长度。
max_element 函数：返回 dp 数组中的最大值，即整个数组中最长递增子序列的长度。

#include <iostream>
#include <vector>
using namespace std;int lengthOfLIS(const vector<int>& nums) {int n = nums.size();if (n == 0) return 0; // 处理空数组的情况vector<int> dp(n, 1); // 初始化dp数组，每个元素代表以对应位置元素结尾的最长递增子序列的长度for (int i = 1; i < n; ++i) {for (int j = 0; j < i; ++j) {if (nums[i] > nums[j]) {dp[i] = max(dp[i], dp[j] + 1); // 更新以nums[i]结尾的最长递增子序列长度}}}return *max_element(dp.begin(), dp.end()); // 返回dp数组中的最大值，即最长递增子序列的长度
}int main() {vector<int> nums = {1, 5, 2, 4, 3}; // 定义一个序列cout << lengthOfLIS(nums) << endl; // 输出最长递增子序列的长度return 0;
}