哈夫曼树
- 哈夫曼树的基本了解
- 哈夫曼树的基本概念
- 创建霍夫曼树的思路
- 编码构建的思路
- 代码实现
- 创建HuffmanTree结点
- 初始化HuffmanTree
- 创建霍夫曼树
- 霍夫曼树编码
哈夫曼树的基本了解
给定 n 个 权值 作为 n 个 叶子节点,构造一颗二叉树,若该树的 带权路径长度(WPL)达到最小,称这样的二叉树为 最优二叉树,也称为 哈夫曼树(Huffman Tree),还有的叫 霍夫曼树
哈夫曼树的基本概念
- 路径 :从树中的一个结点到达另一个节点的分支结构构成的两个点之间的路径
- 路径长度:路径上的分支的数目(例如根结点为第一层,叶子节点为L层,那么根结点到叶子结点之间的路径长度为L-1)
- **树的路径长度:**从树的根结点到每个结点的路径长度之和
- 权:若将树中节点赋给一个有着某种函数的数值,则这个数值称为该节点的 权
- 结点的带权路径长度:从该结点到树根之间路径长度与该结点权重的乘积
- 树的带权路径长度:树中所有的叶子结点的带权路径长度之和
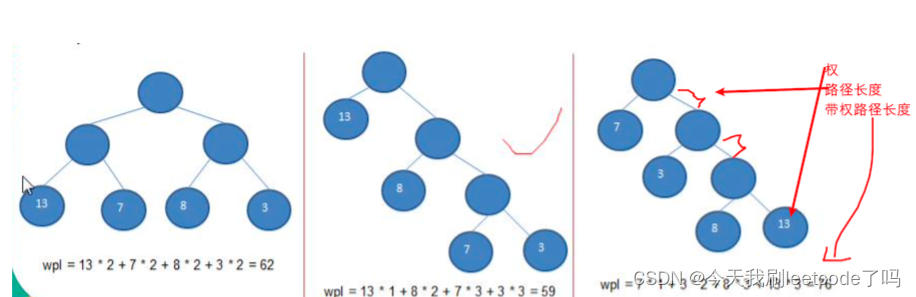
创建霍夫曼树的思路
赫夫曼编码也翻译为 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种 编码方式,,属于一种 程序算法
赫夫曼编码是 赫哈夫曼树 在电讯通信中的经典的应用之一。
赫夫曼编码广泛地用于 数据文件压缩。其压缩率通常在 20%~90% 之间
赫夫曼码是 可变字长编码(VLC) 的一种。Huffman 于 1952 年提出一种编码方法,称之为最佳编码
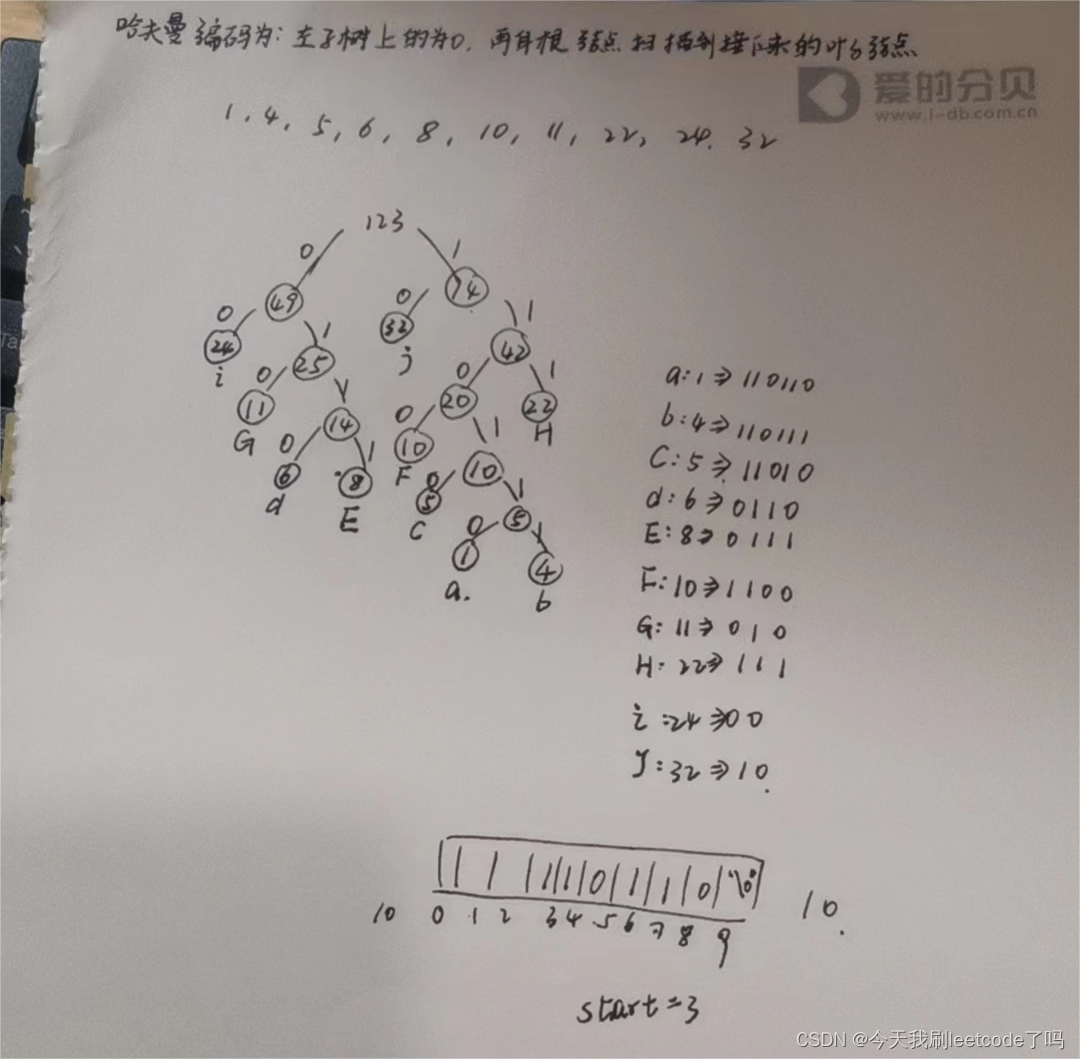
根据已经构建完成的赫夫曼树,给各个字符规定编码(前缀编码):
向左的路径为 0
向右的路径为 1
编码构建的思路

代码实现
创建HuffmanTree结点
#pragma region HuffmanTree的结构定义
typedef int datatype;
typedef struct HuffmanTree
{int weight;/*权重*/datatype data;int parent;int leftchild;int rightchild;
}HTNode;
typedef HuffmanTree* HuffTree;
#pragma endregion
初始化HuffmanTree
HuffTree InitHuffTree(int TreeNum)
{/*初始化树:首先创建存放2*TreeNum的存储空间的树,然后0下标位置不存放数据,从1位置开始赋值权重以及数据。*/HuffTree HT = NULL;HT = (HuffTree)malloc(sizeof(HTNode)*(2 * TreeNum));/*下标为0的HuffmanTree的结点是不用的*/for (int i = 1; i < 2*TreeNum; i++){HT[i].leftchild = -1;HT[i].rightchild = -1;HT[i].parent = -1;/*首先将双亲以及左右孩子置为-1*/}cout << "请输入权重" << endl;for (int i = 1; i <= TreeNum; i++){cin >> HT[i].weight;/*对每个结点赋值权重*/}char c = getchar();cout << "请输入数据" << endl;for (int i = 1; i <=TreeNum; i++){cin >> HT[i].data;}return HT;
}
#pragma endregion
创建霍夫曼树
void minvalue_select(HuffTree HT, int& minloction1, int& minloction2, int loc)
{int minvalue1 = MAXVALUE, minvalue2 = MAXVALUE;for (int i = 1; i < loc; i++){if ((minvalue1 > HT[i].weight)&&(HT[i].parent == -1)){minloction2 = minvalue1;minloction2 = minloction1;minvalue1 = HT[i].weight;minloction1 = i;}else{if ((HT[i].weight <minvalue2)&&(HT[i].parent == -1)){minvalue2 = HT[i].weight;minloction2 = i;}}}
}
HuffTree CreatHuffmanTree(HuffTree HT,int TreeNum)
{/*最终的parent为-1的结点代表根结点 没有双亲*/if (HT == NULL){cout << "HuffmanTree的数据为空 请重新输入" << endl;return NULL;}HuffTree tmpTree = NULL;tmpTree = HT;int minlocation1, minlocation2;for (int i = TreeNum+1; i <= TreeNum*2-1; i++){minvalue_select(tmpTree, minlocation1, minlocation2, i-1);/*找出两个最小的值*/HT[minlocation1].parent = HT[minlocation2].parent = i;HT[i].leftchild = minlocation1;HT[i].rightchild = minlocation2;/*其中location2大于location1*/HT[i].weight = HT[minlocation1].weight + HT[minlocation2].weight;}/*此时i也就是最后一个根结点 它的左右孩子已经确定 但是它的parent为-1 表示它为根结点*/return HT;
}
#pragma endregion
霍夫曼树编码
#pragma region 从叶子结点到根结点逆向求HuffmanTree编码
typedef char** HuffmanCode;
void HuffmanCoding(HuffTree HT, HuffmanCode& HC, int TreeNum)
{HC = (HuffmanCode)malloc(sizeof(char*)*TreeNum);/*表明HC是一个指针类型的变量,同时每一个指针存放的位置为一个char*类型的数据,也就表示HC是一个存放指针类型数据的指针数组*/if (HT==NULL){return;}char* tmpcode = (char*)malloc(sizeof(char)*TreeNum);if (tmpcode == NULL){return;}tmpcode[TreeNum -1 ] = '\0';HuffTree tmpHTree = NULL;tmpHTree = HT;for (int i = 1; i <= TreeNum; i++){int location = TreeNum - 1;int parentIndex = tmpHTree[i].parent;int currentIndex = i;while (parentIndex !=-1)/*未到达根结点*/{if (tmpHTree[parentIndex].leftchild == currentIndex){tmpcode[--location] = '0';}else{tmpcode[--location] = '1';}currentIndex = parentIndex;parentIndex = tmpHTree[parentIndex].parent;}/*完成编码*/HC[i] = (char*)malloc(sizeof(char)*(TreeNum-location));if (HC[i]!=NULL){strcpy(HC[i], tmpcode + currentIndex);}cout << HC[i] << endl;}delete tmpcode;
}
#pragma endregion