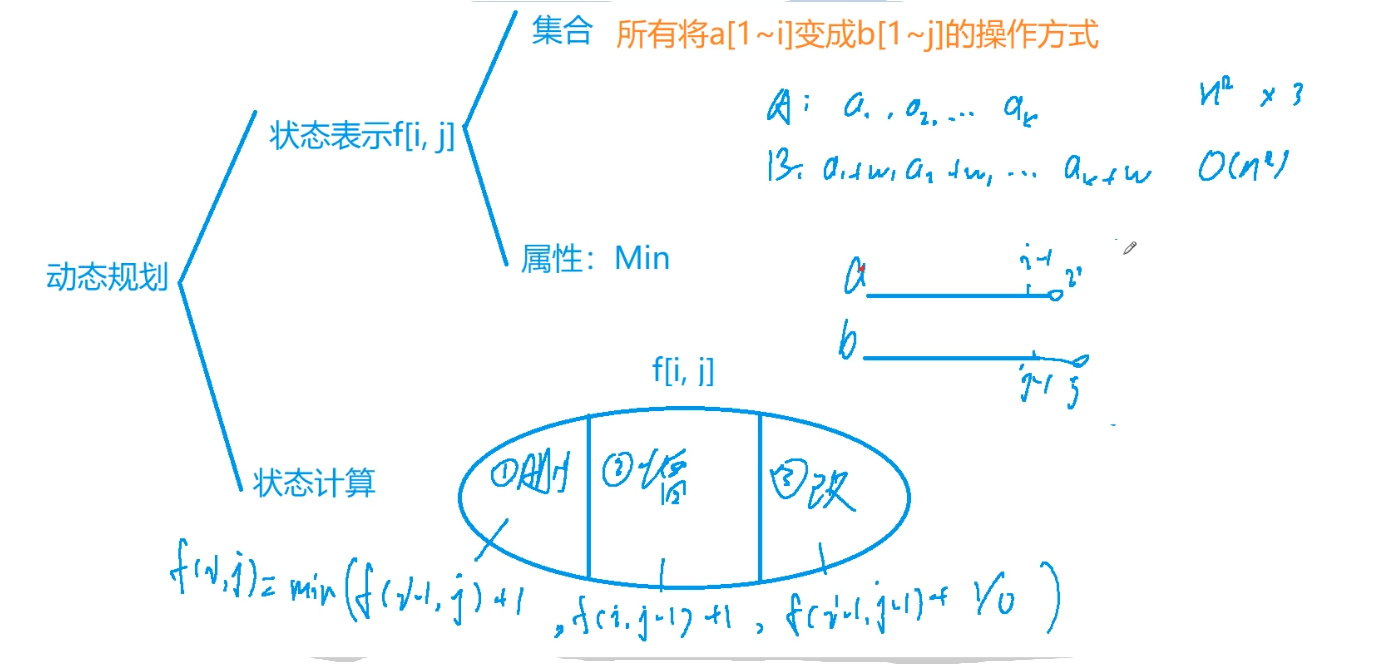
给定两个字符串 A
和 B
，现在要将 A
经过若干操作变为 B
，可进行的操作有：

删除–将字符串 A
中的某个字符删除。
插入–在字符串 A
的某个位置插入某个字符。
替换–将字符串 A
中的某个字符替换为另一个字符。
现在请你求出，将 A
变为 B
至少需要进行多少次操作。

输入格式
第一行包含整数 n
，表示字符串 A
的长度。

第二行包含一个长度为 n
的字符串 A
。

第三行包含整数 m
，表示字符串 B
的长度。

第四行包含一个长度为 m
的字符串 B
。

字符串中均只包含大小写字母。

输出格式
输出一个整数，表示最少操作次数。

数据范围
1≤n,m≤1000
输入样例：
10
AGTCTGACGC
11
AGTAAGTAGGC
输出样例：
4

#include <iostream>
#include <algorithm>using namespace std;const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];int main ()
{scanf("%d", &n);scanf("%s", a + 1); scanf("%d", &m);scanf("%s", b + 1);for(int i = 0; i <= m; i ++ ) f[0][i] = i; // 初始化，只能添加，表示空字符串匹配到b串，有多少个字符就是几步for(int i = 0; i <= n; i ++ ) f[i][0] = i; // 初始化，表示想把a的前i个字母和b的前0个字符匹配，只能删除，有多少个删除几个for(int i = 1; i <= n; i ++ )for(int j = 1; j <= m; j ++ ){f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1); // 前两种情况if(a[i] == b[j]) // 第三种情况，如果a[i] 已经等于b[j]了，就不需要加1了f[i][j] = min(f[i][j], f[i - 1][j - 1]);elsef[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);}printf("%d\n", f[n][m]);return 0;
}