麦肯锡问题解决流程-为希望提升水平的产品经理量身定制-编程知识

您是否想知道世界上最成功的产品经理如何始终如一地提供不仅满足而且超出预期的解决方案？秘密可能就在于世界上最负盛名的咨询公司之一麦肯锡公司所磨练的方法论。本文深入探讨了麦肯锡的问题解决流程，该流程专为希望提升水平的产品经理量身定制。

在动态且经常混乱的产品管理世界中，采用结构化的方法来解决问题不仅是有益的，而且也是有益的。这是必要的。麦肯锡的方法提供了清晰和方向的灯塔。但是什么让它如此有效呢？

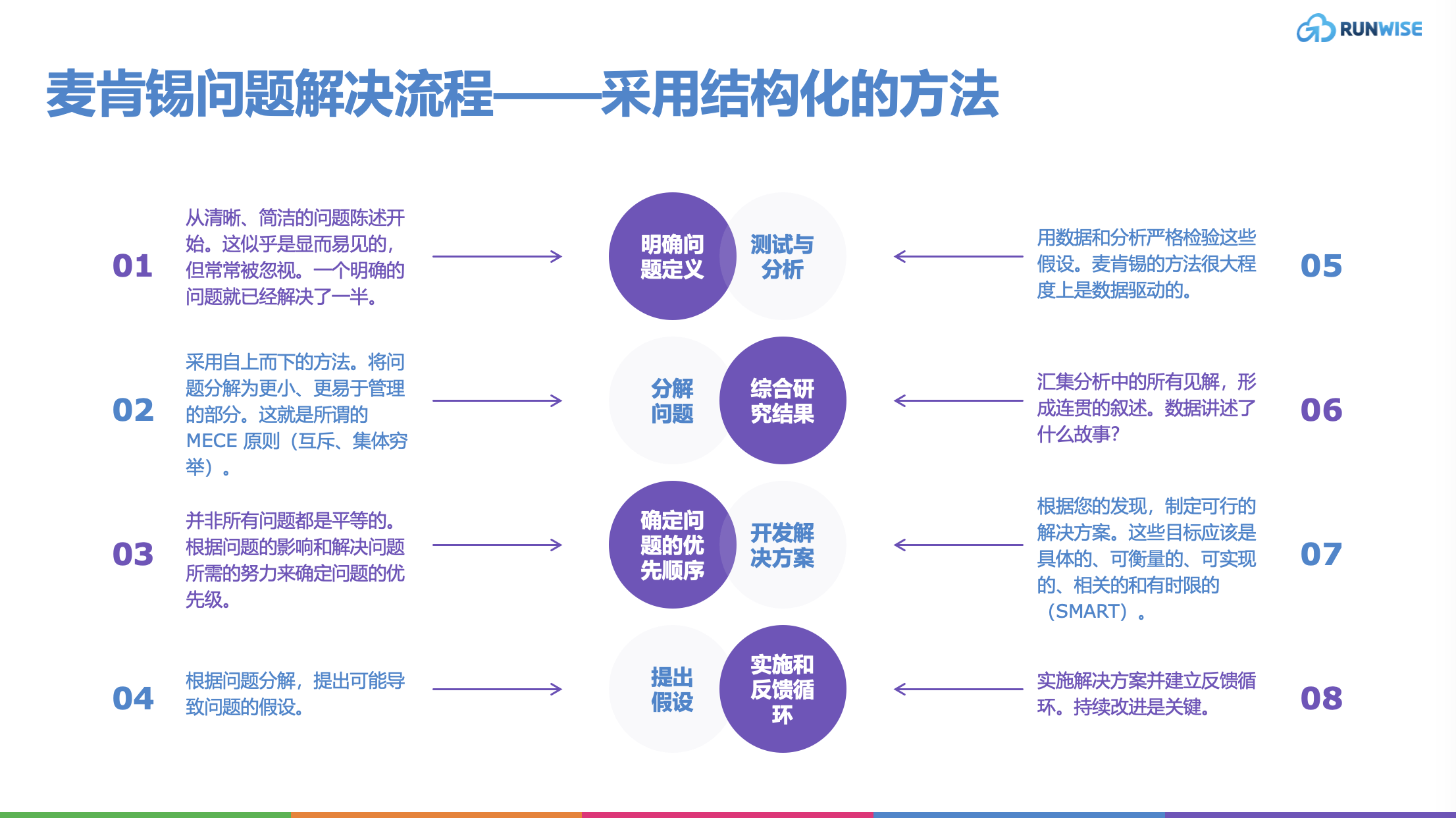
麦肯锡之道：从清晰、简洁的问题陈述开始。这似乎是显而易见的，但常常被忽视。一个明确的问题就已经解决了一半。

实际应用：作为产品经理，当面临挑战时，抵制跳入解决方案模式的冲动。相反，花时间阐明问题。例如，如果您产品的用户参与度正在下降，请确定问题是否与特定功能、用户界面有关，或者可能是与竞争加剧等外部因素有关。

麦肯锡之道：采用自上而下的方法。将问题分解为更小、更易于管理的部分。这就是所谓的 MECE 原则（互斥、集体穷举）。

实际应用：如果问题是用户参与度下降，请将其细分为用户人口统计、使用的功能、在应用程序上花费的时间等类别。这种方法有助于识别需要关注的特定领域。

麦肯锡之道：并非所有问题都是平等的。根据问题的影响和解决问题所需的努力来确定问题的优先级。

实际应用：使用艾森豪威尔矩阵等工具将问题分类为“紧急且重要”、“重要但不紧急”等。这有助于专注于能够产生最重大影响的因素。

麦肯锡之道：根据问题分解，提出可能导致问题的假设。

实际应用：如果用户没有使用新功能，请假设原因。是不是不能满足用户需求？是不是太复杂了？通过调查、A/B 测试或用户访谈来测试这些假设。

麦肯锡之道：用数据和分析严格检验这些假设。麦肯锡的方法很大程度上是数据驱动的。

实际应用：收集支持或反驳你的假设的数据。使用分析工具了解用户行为、进行定性研究并收集反馈。

麦肯锡之道：汇集分析中的所有见解，形成连贯的叙述。数据讲述了什么故事？

实际应用：将定量数据与定性见解相结合，以获得全面的了解。也许数据表明年轻用户对新功能的参与度较低，并且用户访谈显示他们发现它是多余的。

麦肯锡之道：根据您的发现，制定可行的解决方案。这些目标应该是具体的、可衡量的、可实现的、相关的和有时限的（SMART）。

实际应用：如果问题在于功能的复杂性，解决方案可能是简化界面。设定明确的成功指标，例如每日活跃用户的增加或用户满意度得分的提高。

麦肯锡之道：实施解决方案并建立反馈循环。持续改进是关键。

实际应用：分阶段推出变更、监控用户反馈并准备迭代。请记住，解决问题是一个持续的过程，而不是一次性事件。

让我们看一些现实世界的例子，其中这种方法产生了切实的影响：

改进社交媒体应用程序：一家领先的社交媒体公司使用此方法来确定新功能表现不佳的原因。通过数据分析和用户访谈，他们意识到该功能并不直观。基于这些见解的重新设计使功能使用率增加了 30%。
电子商务优化：应用麦肯锡方法解决购物车放弃问题的电子商务平台。通过分解问题，他们发现了关键问题，例如结帐流程冗长和缺乏付款选项。解决这些问题后，购物车放弃率降低了 20%。