有 N 个物品和一个容量是 V 的背包。
物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。
如下图所示：

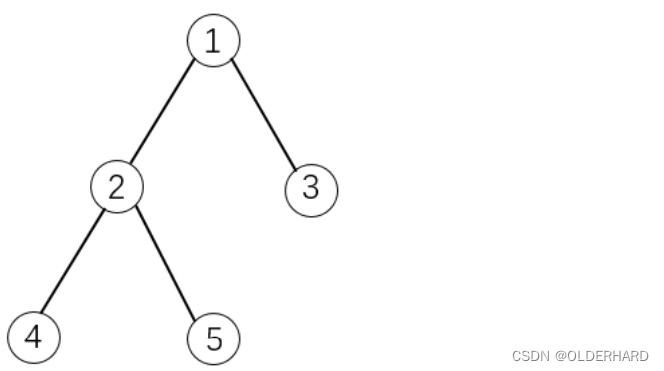
如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。
每件物品的编号是 i，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。

输入
第一行有两个整数 N，V (1 ≤ N,V ≤ 100)，用空格隔开，分别表示物品个数和背包容量。
接下来有 N 行数据，每行数据表示一个物品。第 i 行有三个整数 vi,wi,pi (1 ≤ vi,wi ≤ 100)，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1，表示根节点。 数据保证所有物品构成一棵树。
父节点编号范围：内部结点：1≤pi≤N;根节点 pi=−1;

输出
输出一个整数，表示最大价值。

Input
5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

Output
11

解析：
f[u][j] 表示以 u 为根的子树，在不超过体积 j 的情况下，最大价值是多少。
状态转移：
将 u 的儿子为根节点的子树，看成一个个物品组，将每个物品组按照体积划分0~m，每个物品组最多选择一个。
如果将每个物品组按照选择方案来划分，需要的枚举的数量太大了。
再套层树形DP的板子即可。
 

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=110;
int n,m;
int w[N],v[N];
vector <int> g[N];
int f[N][N];
void dfs (int u)
{for (auto x:g[u])                               //一层循环物品{dfs(x);for (int j=m-v[u];j>=0;j--)                 //二层循环体积，因为根节点 u 是必选的for (int k=0;k<=j;k++)                      //三层循环决策f[u][j]=max(f[u][j],f[u][j-k]+f[x][k]);     //状态转移}for (int j=m;j>=v[u];j--) f[u][j]=f[u][j-v[u]]+w[u];    //每个状态要加上 w[u]for (int j=0;j<v[u];j++) f[u][j]=0;
}
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++){int u;cin>>v[i]>>w[i]>>u;if (u==-1) u=0;g[u].push_back(i);}dfs(0);cout<<f[0][m];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}