归并排序
- 动图演示:

- 基本思想:分治思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
假设我们有左右两块有序区间的数组,可以对它直接进行合并。此时我们需要借助第三方数组,一次比较两块区间的起始位置,把小的那个放到新数组,随后依次比较,小的就放新数组,一直到结束。
但是现在存在一个问题,上述条件是假设了左半区间和右半区间有序,但是原先数组是无序的,也就是左半区间和右半区间均无序。怎么才能达到左半区间和右半区间有序最后再归并成整体有序呢?这就体现到了分治的思想了,将数组一直分,分到1个1个的,归并成有序变成2个2个的,然后归并成有序成4个4个的,最后再4个4个的归并成有序,最终至整体有序。
- 画图解析其完整的归并过程:
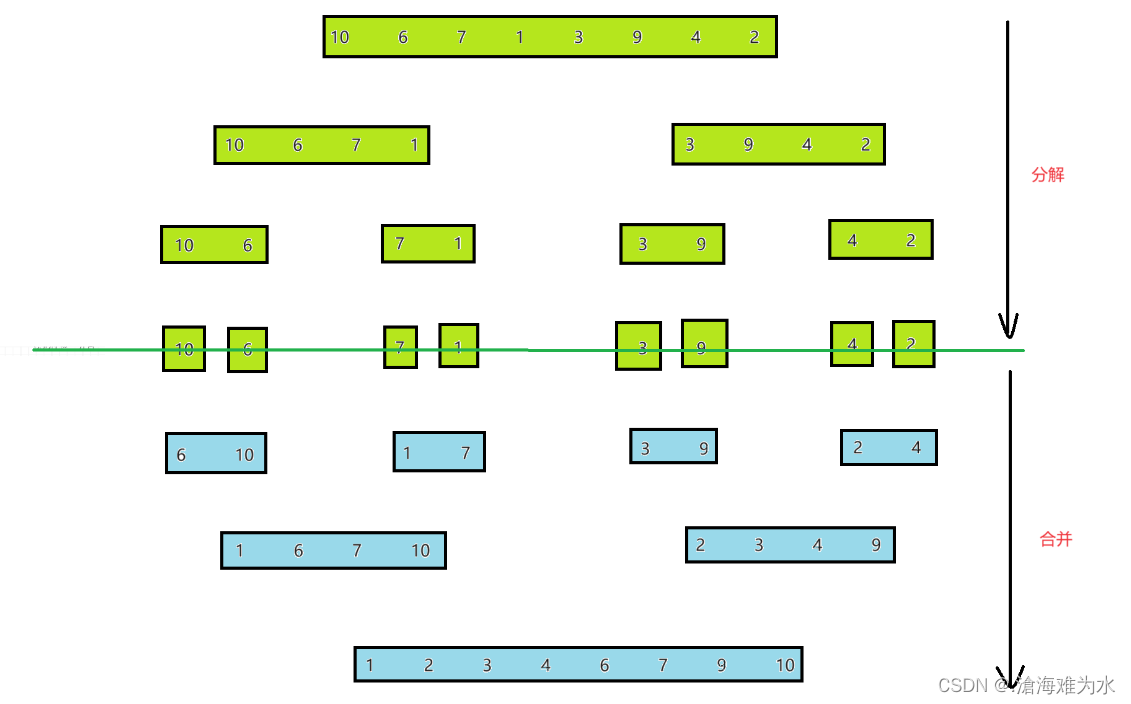
这里我们先用代码实现其分解递归的过程,并用打印法表示其结果:
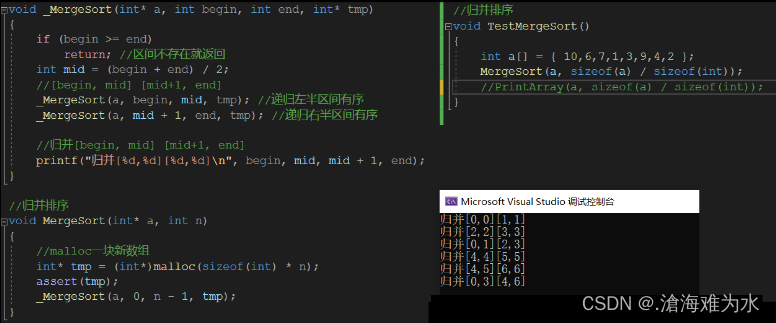
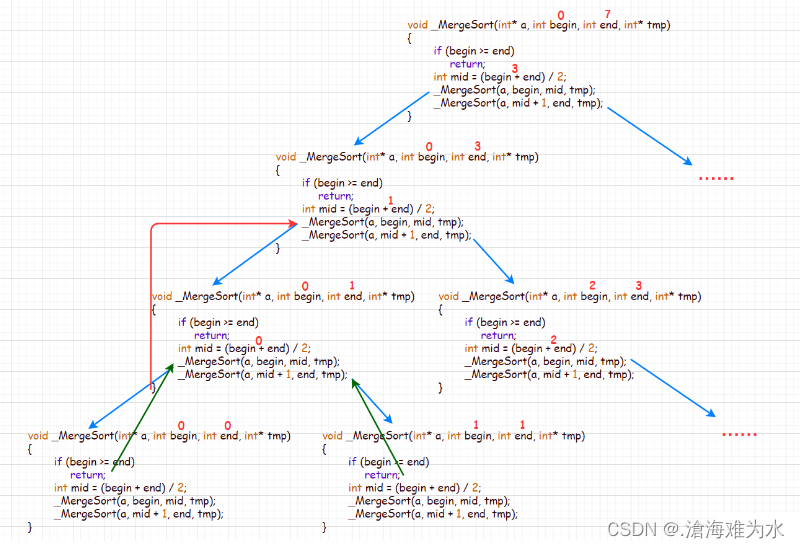
画图演示其部分递归分治的过程:
- 总代码如下:
void _MergeSort(int* a, int begin, int end, int* tmp)
{if (begin >= end)return; //区间不存在就返回int mid = (begin + end) / 2;//[begin, mid] [mid+1, end]_MergeSort(a, begin, mid, tmp); //递归左半_MergeSort(a, mid + 1, end, tmp); //递归右半//归并[begin, mid] [mid+1, end]//printf("归并[%d,%d][%d,%d]\n", begin, mid, mid + 1, end);int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int index = begin;while (begin1 <= end1 && begin2 <= end2){//将较小的值放到tmp数组里头if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}//如若begin2先走完,把begin1后面的元素拷贝到新数组while (begin1 <= end1){tmp[index++] = a[begin1++];}//如若begin1先走完,把begin2后面的元素拷贝到新数组while (begin2 <= end2){tmp[index++] = a[begin2++];}//归并结束后,把tmp数组拷贝到原数组memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}//归并排序
void MergeSort(int* a, int n)
{//malloc一块新数组int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}
归并排序非递归
- 思想:
归并的非递归不需要借助栈,直接使用循环即可。递归版中我们是对数组进行划分成最小单位,这里非递归我们直接把它看成最小单位进行归并。我们可以通过控制间距gap来完成,先看图:
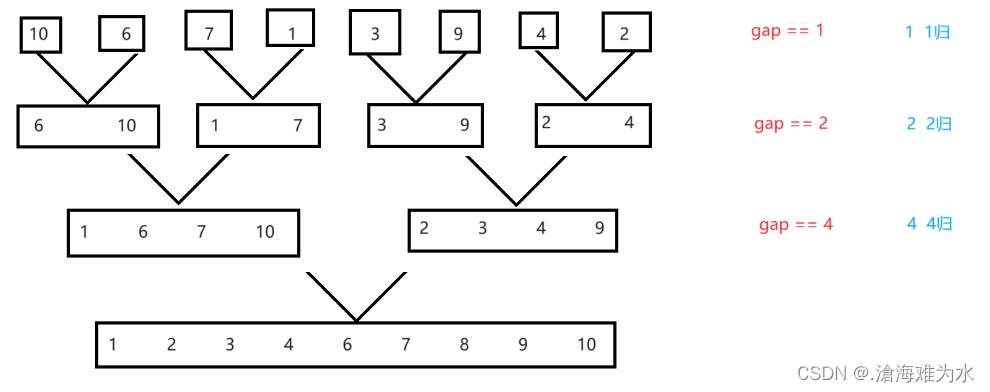
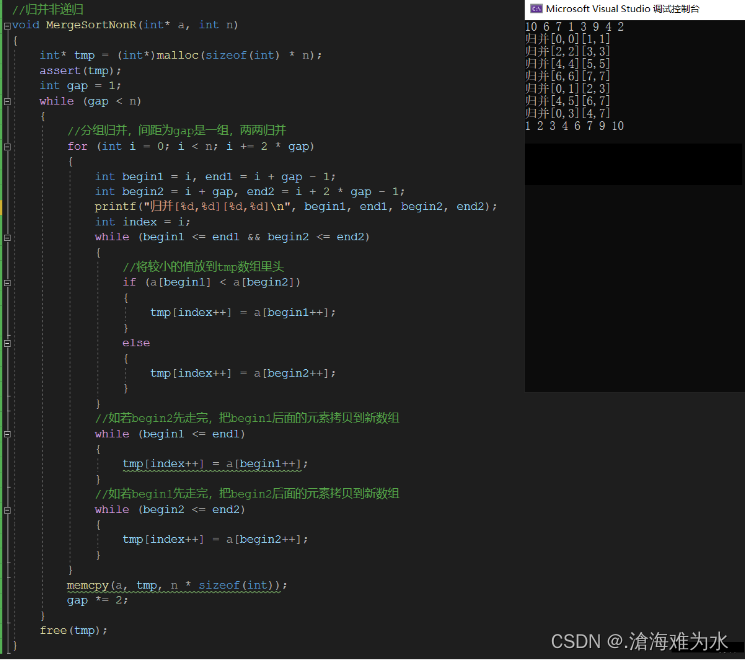
上述情况其实是在理想状态下可行的,只要数组长度不是2的次方倍都会出现问题,先简要看下理想状态下的伪代码,并用printf打印下归并过程:
再强调一遍,只要数组长度不是2的次方倍都会出现问题,像上述长度为8没有问题,那如若长度为6呢?
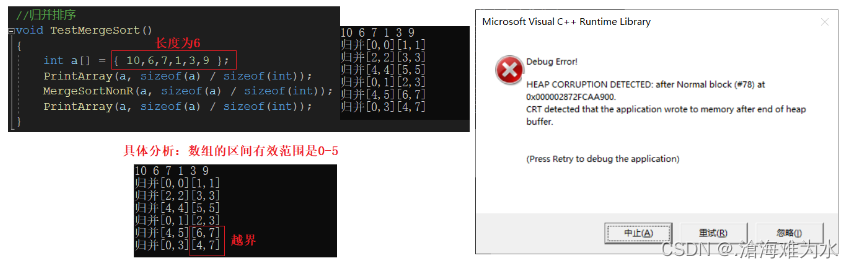
当长度为6不再是2的次方数时就运行出现问题了,综上我们需要考虑下极端情况:根据上述的区间范围,我们可以总结出以下三个可能会出现越界的情况:
- end1越界。
- begin2越界。
- end2越界。
1、end2越界:

2、begin2和end2均越界:

3、end1和begin2和end2均越界 :

综上,我们需要单独对这些极端情况处理。
//end1越界,修正即可
if (end1 >= n)
{end1 = n - 1;
}
//begin2越界,第二个区间不存在
if (begin2 >= n)
{begin2 = n;end2 = n - 1;
}
//begin2 ok,end2越界,修正下end2即可
if (begin2 < n && end2 >= n)
{end2 = n - 1;
}
- 总代码如下:
//归并非递归
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);int gap = 1;while (gap < n){//分组归并,间距为gap是一组,两两归并for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//end1越界,修正即可if (end1 >= n){end1 = n - 1;}//begin2越界,第二个区间不存在if (begin2 >= n){begin2 = n;end2 = n - 1;}//begin2 ok,end2越界,修正下end2即可if (begin2 < n && end2 >= n){end2 = n - 1;}printf("归并[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);int index = i;while (begin1 <= end1 && begin2 <= end2){//将较小的值放到tmp数组里头if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}//如若begin2先走完,把begin1后面的元素拷贝到新数组while (begin1 <= end1){tmp[index++] = a[begin1++];}//如若begin1先走完,把begin2后面的元素拷贝到新数组while (begin2 <= end2){tmp[index++] = a[begin2++];}}memcpy(a, tmp, n * sizeof(int));gap *= 2;}free(tmp);
}
归并排序特性总结
1、归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2、时间复杂度:O(N*logN)。
3、空间复杂度:O(N)。
4、稳定性:稳定 。
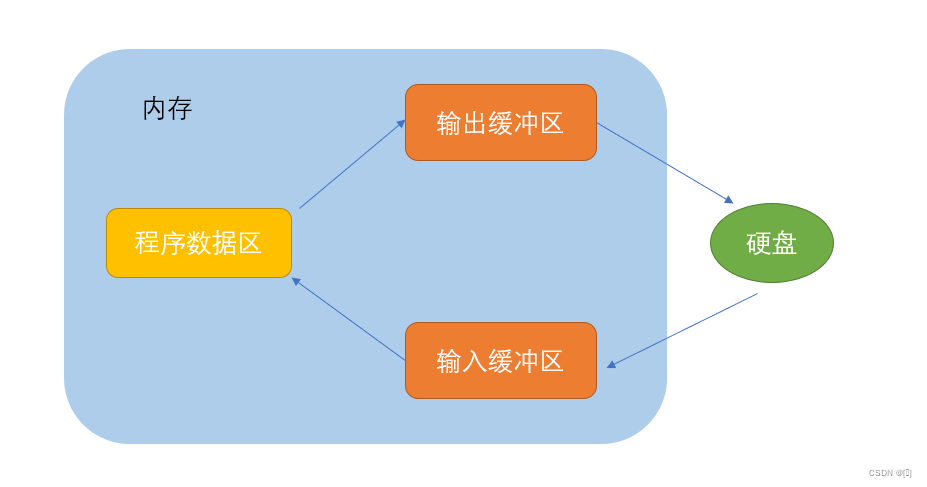
内排序和外排序
在排序中,分为内排序和外排序,简单了解下其概念:
- 内排序:数据量较少,在内存中进行排序。
- 外排序:数据量很大,在磁盘上进行排序。
而我们前面学习的排序中,归并排序既可作为内排序,也可作为外排序,而其它几个排序只能是内排序,这也就说明了在处理数据量很大时,采用归并排序才能解决,其它排序不可。
如若我要排10亿个整数,就只能使用归并排序了,现在来简要算下其占比大小:
- 1G = 1024MB
- 1MB = 1024KB
- 1KB = 1024Byte
- 综上1G = 102410241024Byte,而10亿个整数40亿Byte,所以10亿个整数占4G
现在有10亿个整数(4G)的文件,只给你1G的运行内存,请对文件中的10亿个数进行排序。
核心思想: 数据量大,加载不到内存。想办法控制两个有序文件,两个有序文件归并成一个更大的有序文件。可以把这4G的文件分成4等份,每一份1G,分别读到内存进行归并排序,排完后再写回到磁盘小文件。