拓扑排序入门-编程知识

文章目录

写在前面
一些概念
算法步骤
字典序最大/最小的拓扑序列？
模板
例题
- 3704. 排队
- 家谱树
- 奖金
- P1983 [NOIP2013 普及组] 车站分级
- 1639. 拓扑顺序

写在前面

昨晚cf div3的F就是一道基本上可以说板子的拓扑排序的题目，没有做出来感觉图论很早之前就看了，但是基本没有刷过什么题，开始补一下图论相关的知识点然后做点题目。

一些概念

拓扑序：对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边<u,v>∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。
拓扑排序：由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。
上面是百度百科给出的拓扑序列的解释还是很全面、很能从本质上说明什么是拓扑序的
$图中存在环 == 图不是 D A G == 图没有拓扑序$
一个有向无环图可能存在多种拓扑排序的结果。

算法步骤

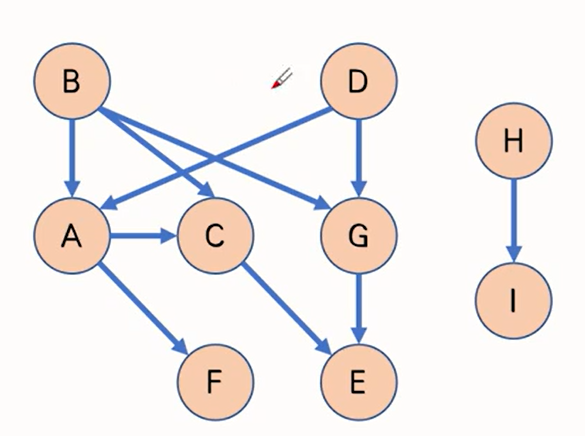
在拓扑排序的过程中，我们用一个数组或者任意容器记录到目前为止的拓扑序列，用一个队列或者任意容器记录所有不在当前拓扑序列中并且入度为0的顶点。

首先遍历整张图上的顶点,如果一个顶点入度为0，将它加入S
当S不为空时：
- 在S中任取一个顶点x，将x加入到q的对位，并把x从S中删去
- 遍历从x出发的边 $x - > y$ ，把这条边删掉，如果y的入度变成了0，则将其加入到S中
循环结束时，如果所有点都加入了q，那么我们就找到了一个合法的拓扑序列，否则可以证明图中存在环

算法的时间复杂度： $O (n + m)$
解释：每个点最多入队一次出队一次，最坏情况是O(n)，对于删边操作，每条边最多被删一次
所以是 $O (n + m)$

字典序最大/最小的拓扑序列？

这字典序最大最小其实实现起来只需要将维护入度为0的点的容器换一下就可以了
我们可以选择优先队列或者set来维护入度为0的点，
就比如我们要求字典序最小的拓扑序列，我们用set去维护，每次从set中拿出的都是当前满足条件的编号最小的入度为0的点，也就是说满足了字典序最小。
最大的话可以重载一下，或者用优先队列（大根堆）来维护入度为0的点。

模板

	//ans用于存储拓扑排序的结果vector<int>ans;//队列保存当前入度为0的点queue<int>q;rep(i,1,n+m){if(!ind[i]){q.push(i);ans.pb(i);}}//bfs求拓扑序的过程，每次取出入度为0的点删除所有出边，如果删除出边导致产生新的入度为0的点//就将这个点加入ans和队列，用于扩展其他点while(q.size()){auto u=q.front();q.pop();for(auto v:g[u]){if(--ind[v.x]==0){q.push(v.x);ans.pb(v.x);}}}

例题

3704. 排队

很裸的一道题目，对于x先于y，我们从x向y连一条边，然后跑一遍拓扑排序就是答案。

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;void solve()
{int n,m;cin>>n>>m;vector<vector<int>>g(n+1);vector<int>ind(n+1);rep(i,1,m){int u,v;cin>>u>>v;g[u].pb(v);ind[v]++;}vector<int>ans;priority_queue<int,vector<int>,greater<int>>q;rep(i,1,n){if(!ind[i]){q.push(i);}}while(q.size()){auto u=q.top();q.pop();ans.pb(u);for(auto v:g[u]){if(--ind[v]==0){q.push(v);}}}for(auto it:ans){cout<<it<<' ';}
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;
//	cin>>_;
//	while(_--)solve();return 0;
}

家谱树

AcWing 1191. 家谱树
基本上是拓扑排序的模板题。
和昨晚div3的F题目很像，所以来补拓扑排序了，多写几遍板子，熟悉起来。
这里提高课的时候视频里回答了一下如何求字典序最小的拓扑序
其实想一下不是很难，最简单的做法就是将普通队列换成优先队列，因为队列存储的是入度为零的点。

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;void solve()
{int n;cin>>n;//vector存图vector<vector<int>>g(n+1);//ind统计每个点的入度vector<int>ind(n+1);rep(i,1,n){int v;while(cin>>v,v){g[i].pb(v);ind[v]++;}}//队列保存一下入度为0的点，并用于更新其他点queue<int>q;//记录拓扑序，如果是数组模拟队列就可以省去这一步vector<int>ans;//将所有入度为0的点入队rep(i,1,n){if(!ind[i]){q.push(i);ans.pb(i);}}//做一遍拓扑排序，也就是一遍bfs的过程while(q.size()){auto u=q.front();q.pop();for(auto v:g[u]){if(--ind[v]==0){q.push(v);ans.pb(v);}}}//输出拓扑序for(auto it:ans){cout<<it<<' ';}
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;
//	cin>>_;
//	while(_--)solve();return 0;
}

奖金

这道题目其实是和dp结合的一道题目。
每一条边 $\rightarrow y$ 都是对于x的约束要求 $x > y$ ，所以出度为0的点也就是汇点是（除了最小值为100）没有其他约束的。
$d [u] = ma x (d [u], d [v] + 1), v 是所有 u 的所有邻点$
我们只需要按拓扑序逆序从后往前递推一遍就能找到每个人奖金的最小值，然后每个点的d相加就是答案

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;
const int mod=1e9+7;void solve()
{int n,m;cin>>n>>m;vector<vector<int>>g(n+1);vector<int>ans;vector<int>ind(n+1);rep(i,1,m){int u,v;cin>>u>>v;g[v].pb(u);ind[u]++;}queue<int>q;rep(i,1,n){if(!ind[i]){q.push(i);ans.pb(i);}}while(q.size()){auto u=q.front();q.pop();for(auto v:g[u]){if(--ind[v]==0){q.push(v);ans.pb(v);}}}if(ans.size()!=n){cout<<"Poor Xed"<<endl;return;}else{vector<int>d(n+1,100);for(auto u:ans){for(auto v:g[u]){if(d[u]+1>d[v]){d[v]=d[u]+1;}}}int res=0;rep(i,1,n){res+=d[i];}cout<<res<<endl;}
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;
//	cin>>_;
//	while(_--)solve();return 0;
}

P1983 [NOIP2013 普及组] 车站分级

这道题目有点和上面的奖金类似，和差分约束这些知识点密切相关。
分析一趟车次，对于这趟车中，所有停靠站的优先级必然高于没有停靠的，这样就会有一个关系
$a_停>=a_{不停}+1$ 这个关系很像差分约束中的关系
对于一趟车次，就分为了停靠和不停靠这两类
以题目中给出的样例的第一趟车表示

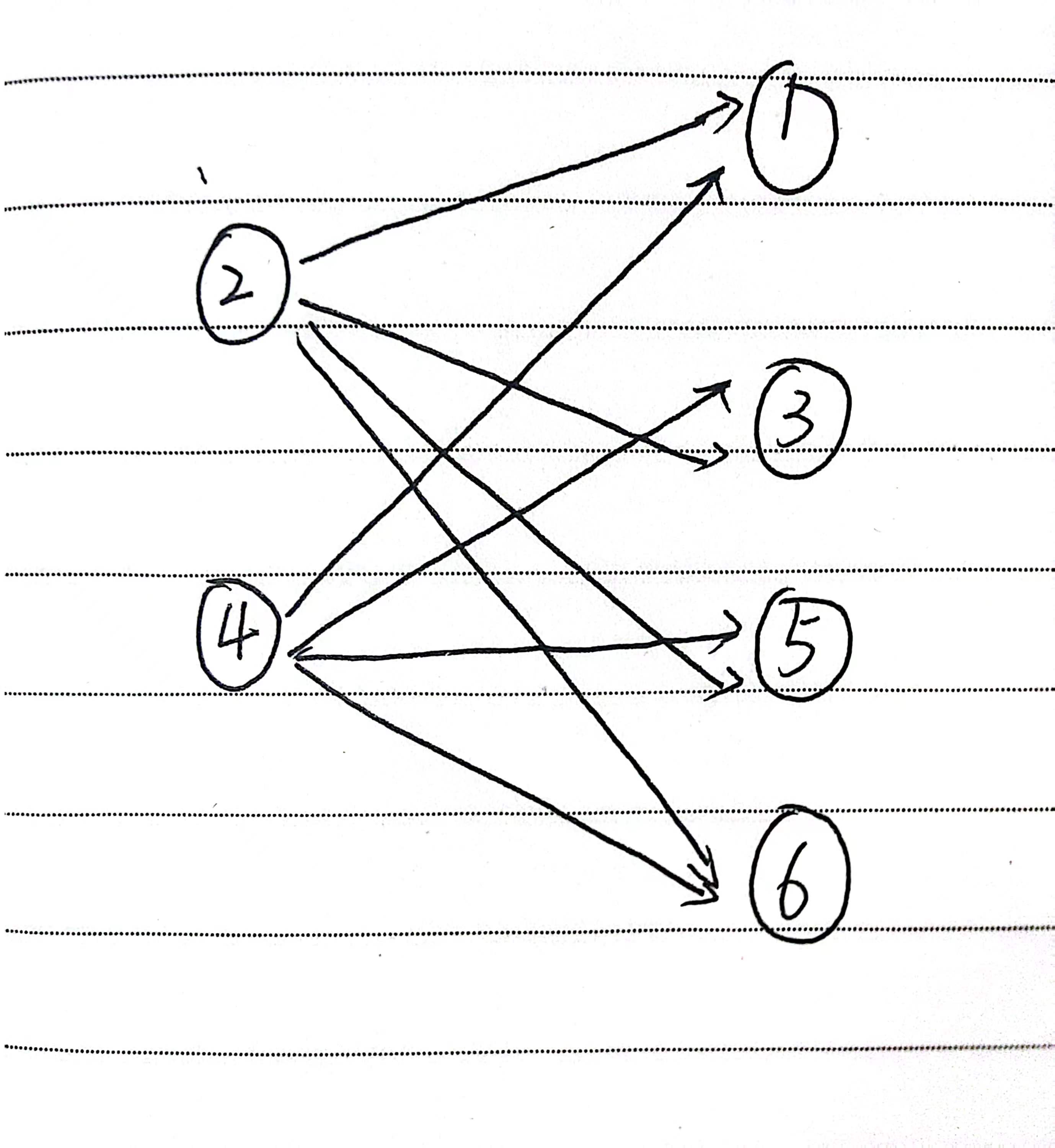
边权为1。
然后按拓扑序跑一遍最长路，求的就是每个点的最长路的最大值。
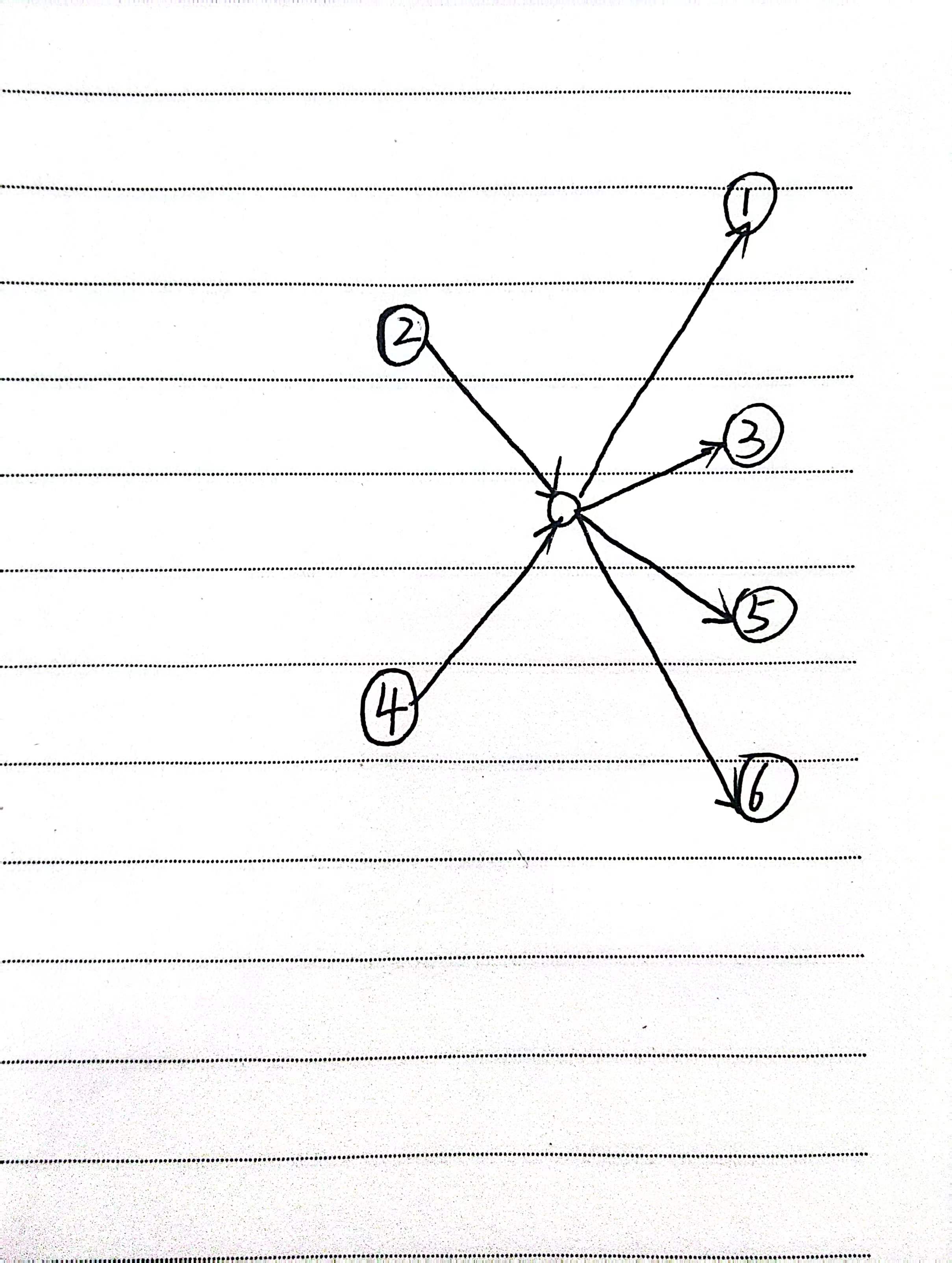
这里由于连边很多而且是一个集合的所有点和另一个集合的所有点都连的有边，两边点的个数假设为 $n 、 m$ 那么，边数就是 $nm$ 很多
可以这样建边去优化，类似交换机的原理（hh学过计网的知识用上了），这样就把边数优化成了 $m + n$ 还是很巨大的一个优化的。

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;void solve()
{int n,m;cin>>n>>m;vector<vector<pii>>g(n+m+1);vector<int>ind(n+m+1);rep(i,1,m){vector<int>st(n+1,0);int start=n,ed=1,k;cin>>k;while(k--){int tmp;cin>>tmp;st[tmp]=1;start=min(start,tmp);ed=max(ed,tmp);}rep(j,start,ed){if(!st[j]){g[j].pb({i+n,0});ind[i+n]++;}else{g[i+n].pb({j,1});ind[j]++;}}}vector<int>ans;queue<int>q;rep(i,1,n+m){if(!ind[i]){q.push(i);ans.pb(i);}}while(q.size()){auto u=q.front();q.pop();for(auto v:g[u]){if(--ind[v.x]==0){q.push(v.x);ans.pb(v.x);}}}vector<int>d(n+m+1,0);rep(i,1,n)	d[i]=1;for(auto u:ans){for(auto v:g[u]){d[v.x]=max(d[v.x],d[u]+v.y);}}int res=0;rep(i,1,n){res=max(res,d[i]);}cout<<res<<endl;
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;
//	cin>>_;
//	while(_--)solve();return 0;
}

1639. 拓扑顺序

暴力地去判断每个序列是否合法即可
对于每个序列我们判断在删完所有入边以后是否入度为0，如果为不0则说明拓扑序列不合法，反之则一直去删边，知道检查完最后一个点，均满足每个点在上一个点删完所有边之后入度为0，则说明是合法的拓扑序列。

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_backusing namespace std;void solve()
{int n,m;cin>>n>>m;vector<vector<int>>g(n+1);vector<int>ind(n+1);rep(i,1,m){int u,v;cin>>u>>v;g[u].pb(v);ind[v]++;}int k;cin>>k;rep(i,0,k-1){vector<int>d(ind);vector<int>a(n+1);rep(j,1,n){cin>>a[j];}bool st=true;rep(j,1,n){if(d[a[j]]){st=false;break;}for(auto v:g[a[j]]){d[v]--;}}if(!st){cout<<i<<' ';}}
}signed main(){ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);int _;
//	cin>>_;
//	while(_--)solve();return 0;
}