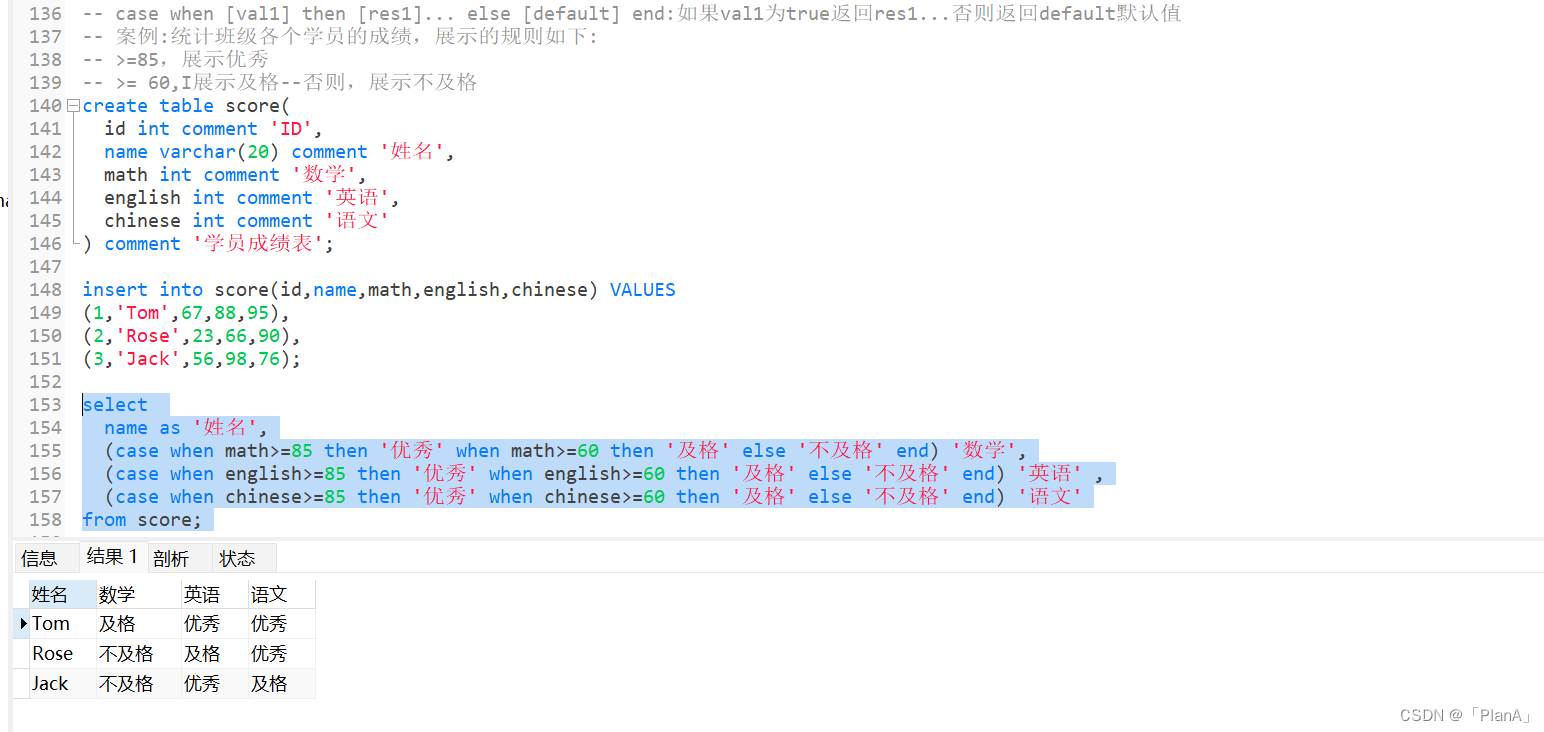
455.分发饼干
很简单的思路:小孩和饼干分别排个序,逐个匹配即可
确实有那种感觉了:这也叫算法吗?(
int findContentChildren(vector<int>& g, vector<int>& s) {std::sort(g.begin(), g.end());std::sort(s.begin(), s.end());int ans = 0;for (int gIndex = 0, sIndex = 0; gIndex < g.size() && sIndex < s.size();) {// 吃得饱就吃,吃不饱就看下一块稍大点的够不够吃饱if (s[sIndex] >= g[gIndex]) {++ans;++gIndex;++sIndex;}else {++sIndex;}}return ans;
}376.摆动序列
开始没看清楚题意写成最长连续子序列了、
最长连续子序列
int wiggleMaxLength(vector<int>& nums) {if (nums.size() == 1)return 1;bool pre = false;int ans = 1;int count = 0;for (int i = 1; i < nums.size(); ++i) {int diff = nums[i] - nums[i - 1];if (diff == 0) {count = 0;continue;}bool cur = diff > 0;if (count == 0) {count = 2;}else if(pre + cur == 1) {++count;if (count > ans)ans = count;}else {count = 1;}pre = cur;}return ans;
}为了保持连续,需要额外判断什么时候对序列进行切割,参数的初始化也更麻烦。
题意理解错了,就当多做了道扩展题吧(
写完发现不对啊,不需要是连续的。想了半天脑子没转过弯,找了文字解析看到图一眼就明白了:
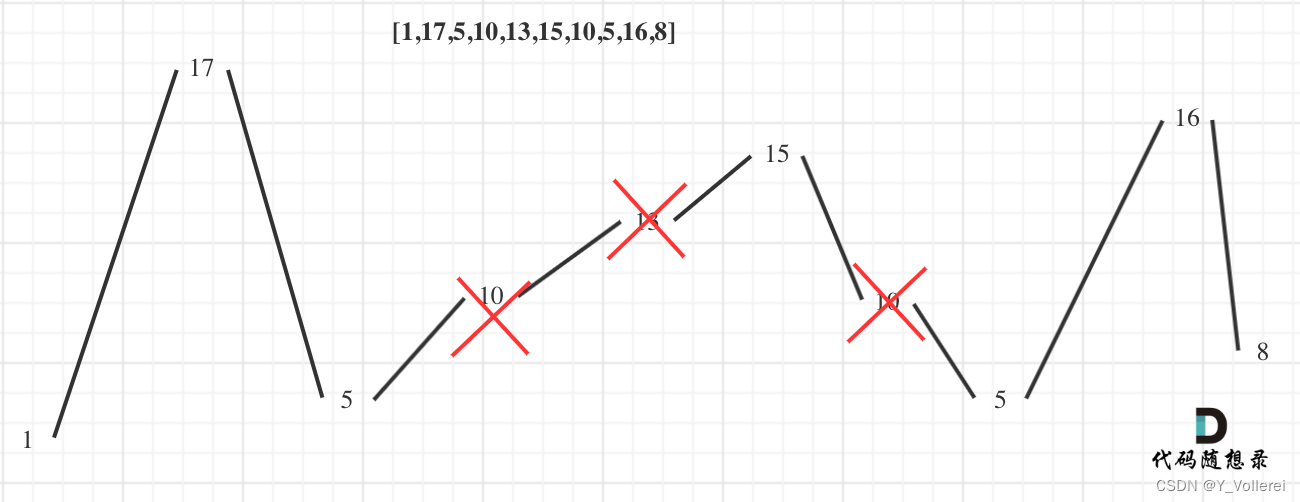
简单来说——计算转折点数量即可
思路非常简单,但写起来还是有一些细节的,比如diff==0时是需要特殊处理的(我的写法中cur和pre都设置为了bool,>0时为true,false其实对应了<0和==0两种情况,所以需要单独处理)
(写完发现这不比连续子序列简单多了)
int wiggleMaxLength(vector<int>& nums) {if (nums.size() == 1)return 1;bool pre;int ans = 1;for (int i = 1; i < nums.size(); ++i) {int diff = nums[i] - nums[i - 1];// 相等直接跳过(解决相等时cur的判定问题)if (diff == 0)continue;bool cur = diff > 0;// pre + cur == 1表示两者异或,此时为折角if (ans == 1 || pre + cur == 1) {++ans;// 只有在折角处才更新prepre = cur;}}return ans;
}53.最大子数组和
(过于简单,不禁感叹中等题间亦有差距)
这题的关键是想明白什么情况下需要切割之前的序列:当 总和小于0 且 当前元素大于总和 时切割之前的序列
(写出来一共没几行,直到AC出来前一刻还在想应该没有这么简单吧)
int maxSubArray(vector<int>& nums) {int ans = nums[0];int sum = nums[0];for (int i = 1; i < nums.size(); ++i) {// 当sum小于0且当前值大于sum时舍弃之前的所有元素if (sum < 0 && nums[i] > sum)sum = nums[i];// 其他情况无脑累加即可elsesum += nums[i];// 记录过程中的最大值if (sum > ans)ans = sum;}return ans;
}总结
第一天做贪心,感觉是真的奇妙,有思路就简单到怀疑人生,脑子拐不过弯就死活想不出。再品几天看看能不能品出点啥。