cordic算法圆周系统计算sin、cos、平方和开根、atan
- 一、cordic圆周系统旋转模式和向量模式
- 1.1 旋转模式
- 1.2 向量模式
- 二、一些需要考虑的事项
- 2.1角度范围
- 2.2输入正负
- 2.3关于迭代精度
- 2.4坐标系旋转
- 参考文献:
若想计算 s i n sin sin、 c o s cos cos、 x 2 + y 2 \sqrt{x^2+y^2} x2+y2、 a t a n atan atan、坐标系旋转等复杂的数学运算,cordic算法提供了一种逼近的思想。cordic的圆周系统可以较精准的求解出上述数学运算,它将复杂的三角函数等数学运算通过迭代的方式分解为移位和加法,最终逼近所需要的求解精度。
一、cordic圆周系统旋转模式和向量模式
关于cordic算法的背景和理论网上已经有大量的参考文献,此处仅仅简述cordic算法的工作模式:
1.1 旋转模式
旋转模式的思想就是想通过旋转的方式,初始化 x 0 = K x_0=K x0=K, y 0 = 0 y_0=0 y0=0, z 0 = θ z_0=\theta z0=θ,每次迭代通过 z i z_i zi值的正负性确定旋转方向,将已知的角度值 z 0 z_0 z0通过不断的迭代,逐渐逼近到 z n = 0 z_n=0 zn=0的过程。最终 x n = c o s θ x_n=cos \theta xn=cosθ, y n = s i n θ y_n=sin \theta yn=sinθ, θ ∈ ( − π ∼ π ) \theta\in(-\pi \sim \pi) θ∈(−π∼π)。
1.2 向量模式
向量模式的思想就是初始化 x 0 = A x_0=A x0=A, y 0 = B y_0=B y0=B, z 0 = 0 z_0=0 z0=0,每次迭代通过 y i y_i yi值的正负性确定旋转方向,最终使初始向量旋转至 x x x轴的正半轴,使 y n y_n yn趋向于 0 0 0。最终 x n = A 2 + B 2 x_n=\sqrt{A^2+B^2} xn=A2+B2, y n = a r c t a n ( B A ) y_n= arctan(\frac{B}{A}) yn=arctan(AB)。
二者模式的对比如下:
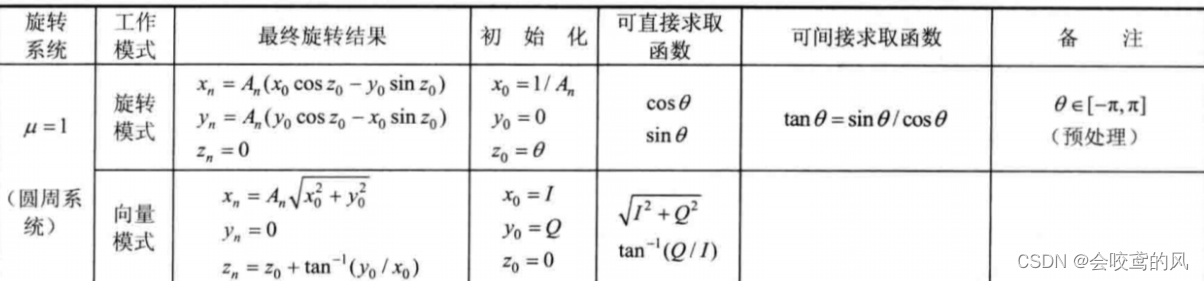
二、一些需要考虑的事项
2.1角度范围
旋转模式的目标旋转角度 θ i \theta_i θi的取值范围是 [ − 99.8829 ° ∼ 99.8829 ° ] [-99.8829\degree \sim 99.8829\degree] [−99.8829°∼99.8829°] ,而计算sin、cos大部分需要的角度要大于此角度,因此可通过正余弦定理将第一二三四象限的角度全部统一到第一象限,即0-90度。即可满足 [ − 180 ° ∼ 180 ° ] [-180\degree \sim 180\degree] [−180°∼180°] 的实际项目需要。计算arctan的角度需要的范围完全满足,因此不需要特殊处理。
2.2输入正负
当求解 x 2 + y 2 \sqrt{x^2+y^2} x2+y2时,注意输入的x,y值建议为正数,若为signed值,建议将负数转化成正数。实测发现当输入为负数时,求得的结果的误差较输入全正数时大的多。
2.3关于迭代精度
因项目要求,需要尽可能的减少资源,因此要求在保证精度的前提下通过减少迭代次数等方式进行优化来降低资源占用。
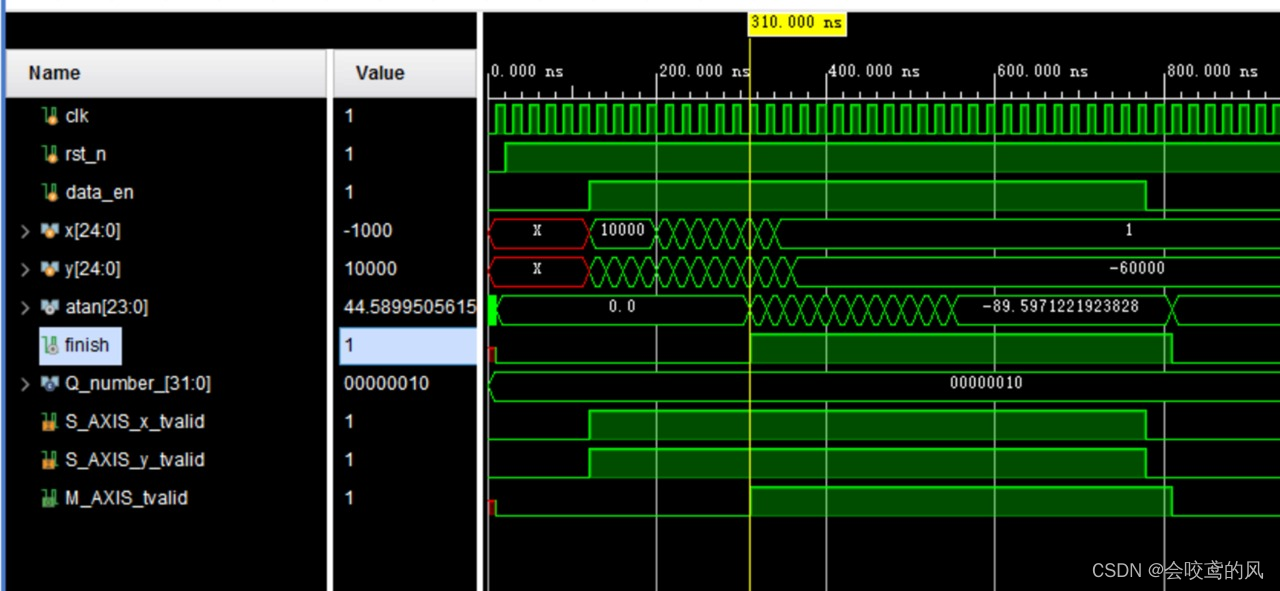
在迭代精度上,以求解 a t a n atan atan的精度为例:当迭代16次时,求解 a r c t a n 1 arctan1 arctan1 的角度值如图1所示,能精确到小数点后两位。经过实测,如图2所示,当迭代8次时,通过四舍五入的方式求得的角度值基本符合项目要求(要求数值精确到整数)。
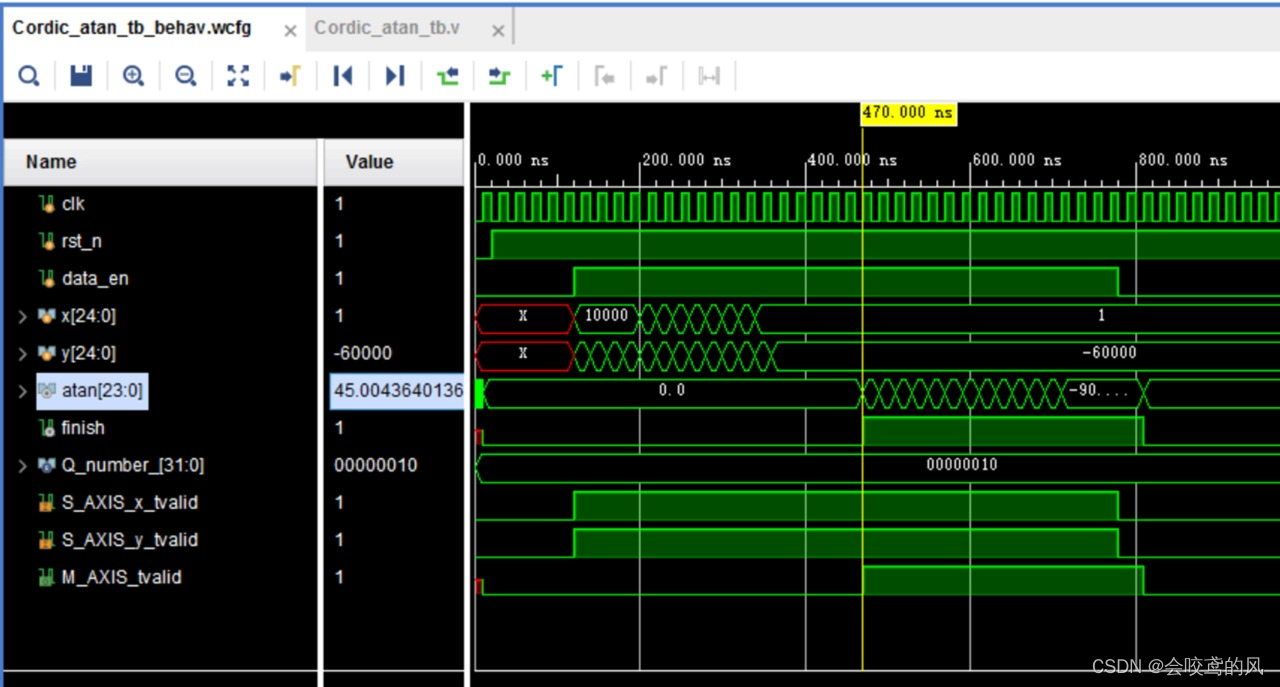
例2: 求解 1 2 + 1 2 \sqrt{1^2+1^2} 12+12迭代16次的精度如图3所示, 精度非常高:
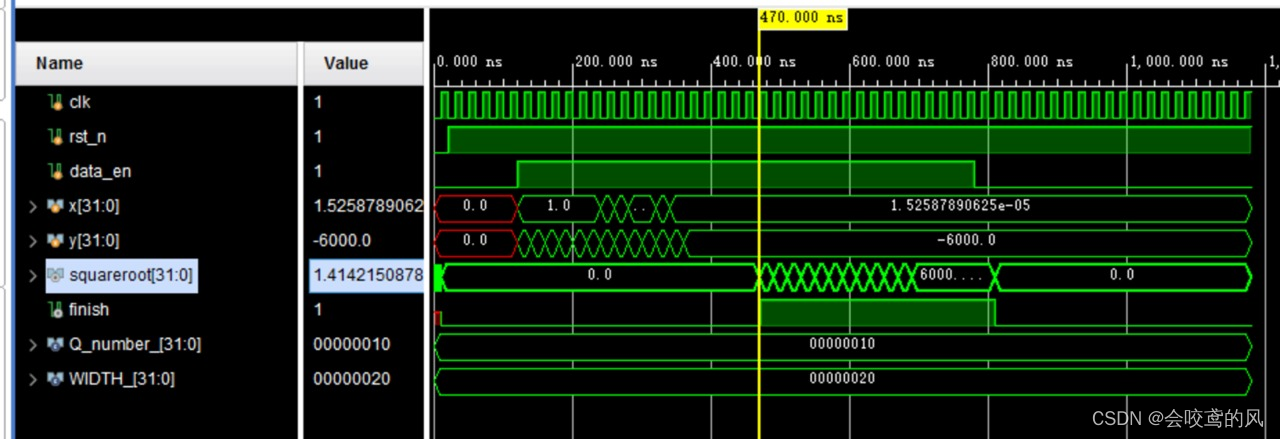
2 \sqrt{2} 2的理论值如下:

2.4坐标系旋转
由于多个雷达的点云数据需要统一到同一个坐标系下进行计算,因此用到了坐标系旋转。该算法也可利用Cordic算法思想进行求解,此时输入为 x 0 x_0 x0、 y 0 y_0 y0、 θ \theta θ,输出取 x n x_n xn、 y n y_n yn。迭代方程此时变为:
{ x n = K ( x 0 + d i y 0 2 − i ) y n = K ( y 0 − d i y 0 2 − i ) \left\{ \begin{matrix} x_n=K(x_0+d_i y_0 2^{-i}) \\ y_n=K(y_0-d_i y_02^{-i}) \end{matrix} \right. {xn=K(x0+diy02−i)yn=K(y0−diy02−i)
将原有的Cordic算法稍作更改即可实现。
参考文献:
流水线求sincos:
https://blog.csdn.net/u010712012/article/details/77755567
坐标系旋转:
https://zhuanlan.zhihu.com/p/631899064
https://zhuanlan.zhihu.com/p/41263701
流水线求arctan:
https://blog.csdn.net/zwl_liang/article/details/104885263
开源ip核:
https://opencores.org/projects/cordic_atan_iq