莫愁千里路
自有到来风
CSDN 请求进入专栏 X
是否进入《C++专栏》?
确定
目录
线性dp简介
斐波那契数列模型
第N个泰波那契数
思路:
代码测试:
三步问题
思路:
代码测试:
最小花费爬楼梯
思路:
代码测试:
路径问题
数字三角形
思路:
代码测试:
不同路径
思路:
代码测试:
LIS模型
最长递增子序列
思路:
代码测试:
线性dp简介
线性DP(Introduction)
线性DP是动态规划问题中的一类问题,指状态之间有 线性关系 的动态规划问题
DP解题套路
<1>根据题意列出状态表示dp表里面的值所代表的含义
分析问题的过程中发现重复子问题
<2>根据状态表示列出状态转移方程dp[i]等于什么
<3>初始化填dp表的时候不能越界访问
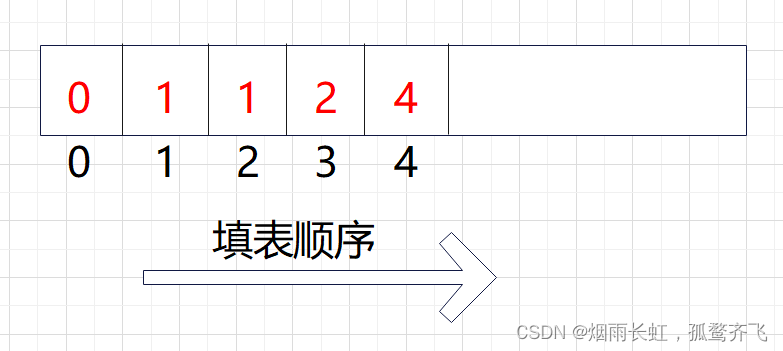
<4>填表顺序递推求解的顺序
斐波那契数列模型
第N个泰波那契数
题目链接:第N个泰波那契数
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数
n,请返回第 n 个泰波那契数 Tn 的值。示例 1:
输入:n = 4 输出:4 解释: T_3 = 0 + 1 + 1 = 2 T_4 = 1 + 1 + 2 = 4示例 2:
输入:n = 25 输出:1389537提示:
0 <= n <= 37- 答案保证是一个 32 位整数,即
answer <= 2^31 - 1
思路:
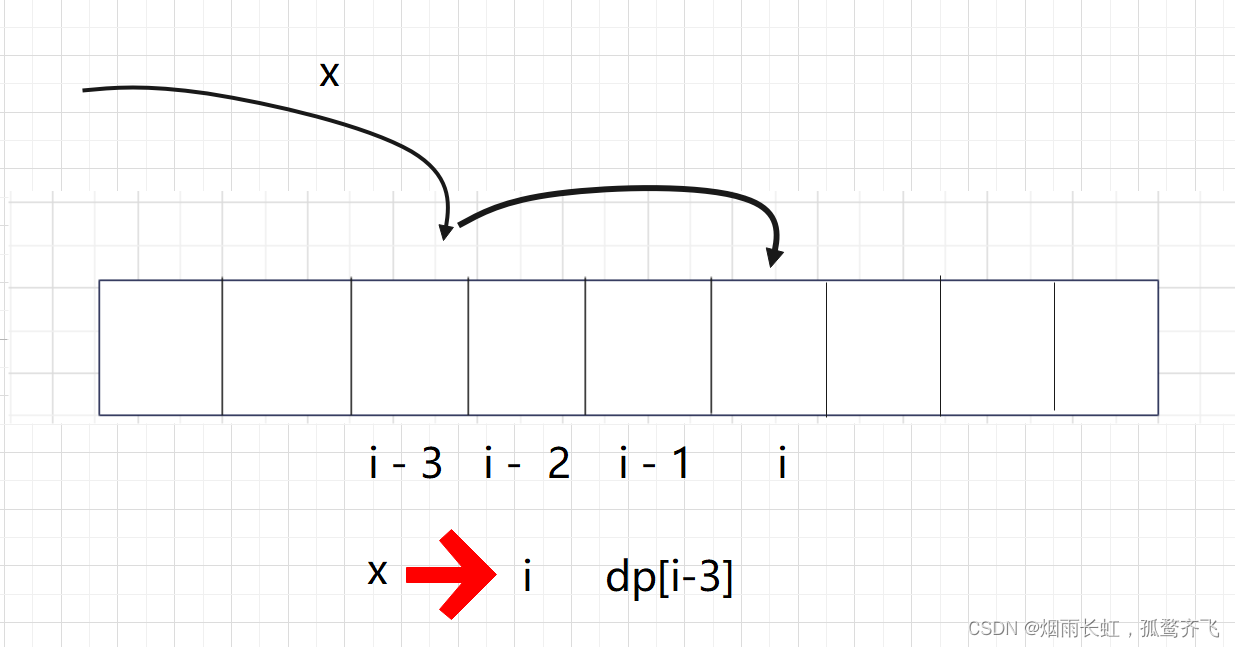
<1>状态表示 dp[i]表示第 i 个泰波那契数的值 <2>状态转移方程 dp[i] = dp[i-1] + dp[i-2] + dp[i-3] (Tn+3 = Tn + Tn+1 + Tn+2) <3>初始化 dp[0] = 0,dp[1] = dp[2] = 1 <4>填表顺序 从左至右
代码测试:
时间复杂度O(N)
空间复杂度O(N)
class Solution { public:int tribonacci(int n) {//防止数组越界if(n == 0) return 0;if(n == 1||n == 2) return 1;vector<int> dp(n+1);//初始化dp[0] = 0,dp[1] = dp[2] = 1;//顺序填表for(int i = 3;i<=n;i++)//状态转移方程dp[i] = dp[i-1]+dp[i-2]+dp[i-3];return dp[n];} };
三步问题
题目链接:三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3 输出:4 说明: 有四种走法示例2:
输入:n = 5 输出:13提示:
- n范围在[1, 1000000]之间
思路:
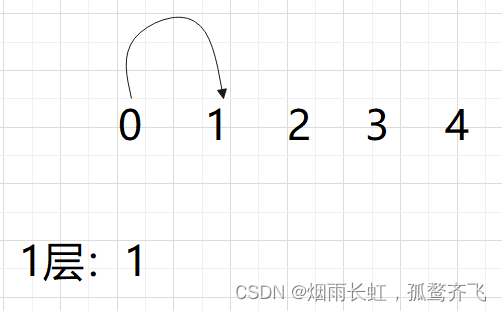
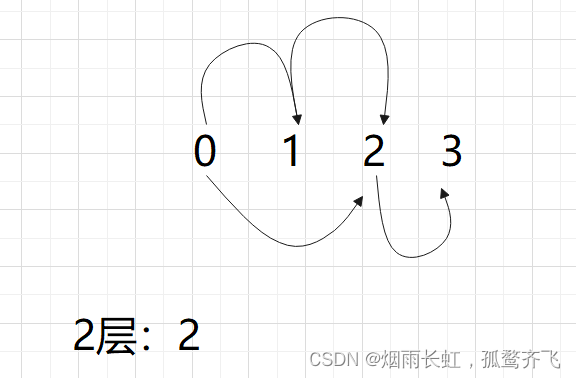
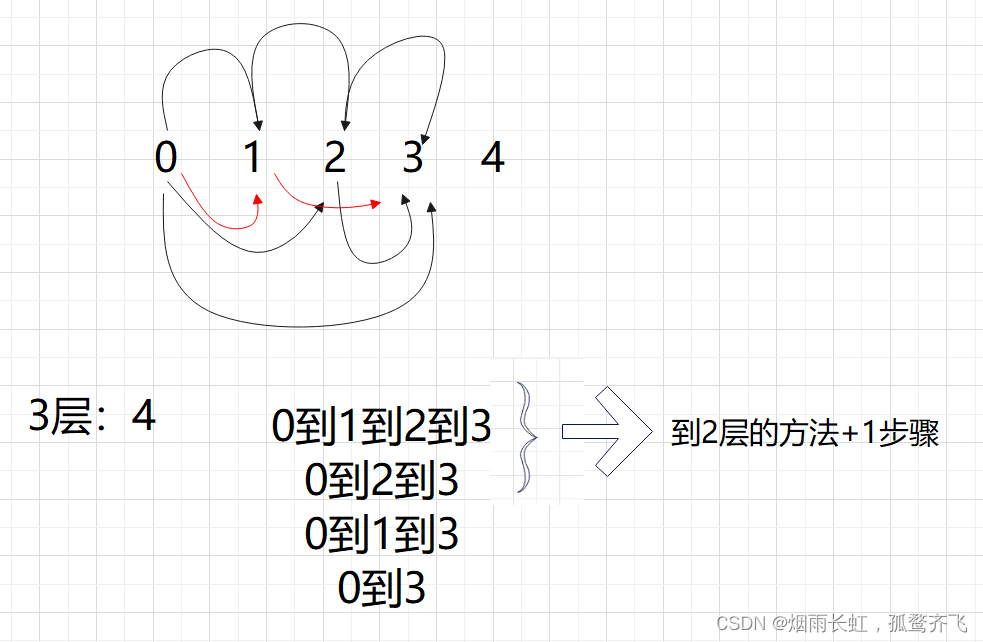
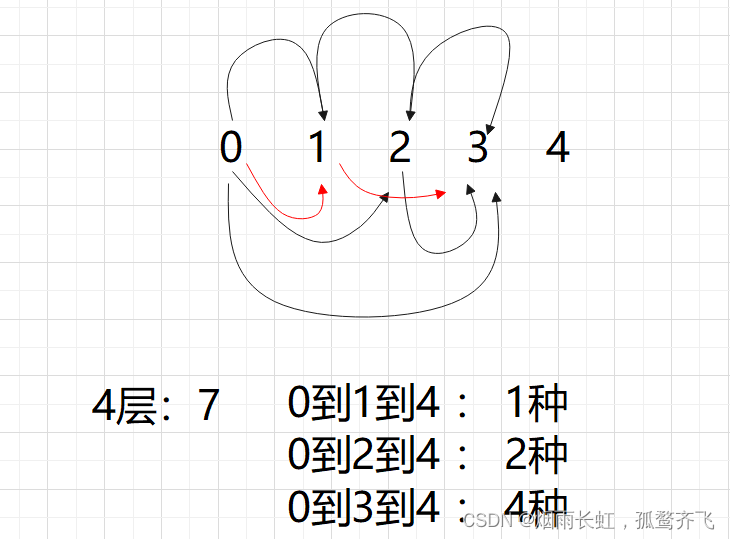
我们发现从 4 层开始就是前三项之和,第五层就是:7 + 4 + 2= 13
所以从第四层开始,满足斐波那契规律
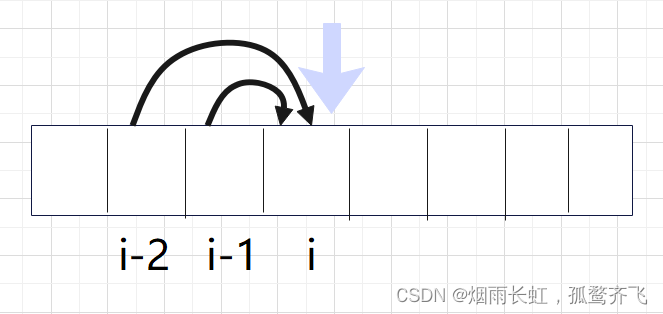
<1>状态表示 以 i 为结尾,dp[i]表示到达 i 位置时,一共有多少种方法 <2>状态转移方程 以 i 的位置的状态,最近的一步开始划分问题
从(i-1)到 i:dp[i-1]
从(i-2)到 i:dp[i-2]
从(i-3)到 i:dp[i-3]
dp[i] = dp[i-1]+dp[i-2]+dp[i-3]
<3>初始化 dp[1] = 1,dp[2] = 2,dp[3] = 4 <4>填表顺序 从左往右 代码测试:
时间复杂度O(N)
空间复杂度O(N)
class Solution { public:int waysToStep(int n) {//取模数据const int MOD = 1e9+7; //边界问题if(n == 1||n == 2) return n;if(n == 3) return 4;vector<int> dp(n+1);//初始化dp[1] = 1,dp[2] = 2,dp[3] = 4;//顺序填表for(int i = 4;i<=n;i++)//状态转移方程+取模操作dp[i] = ((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;return dp[n];} };
最小花费爬楼梯
题目链接:最小花费爬楼梯
数组的每个下标作为一个阶梯,第
i个阶梯对应着一个非负数的体力花费值cost[i](下标从0开始)。每当爬上一个阶梯都要花费对应的体力值,一旦支付了相应的体力值,就可以选择向上爬一个阶梯或者爬两个阶梯。
请找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
示例 1:
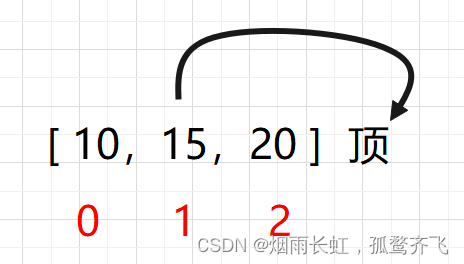
输入:cost = [10, 15, 20] 输出:15 解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。示例 2:
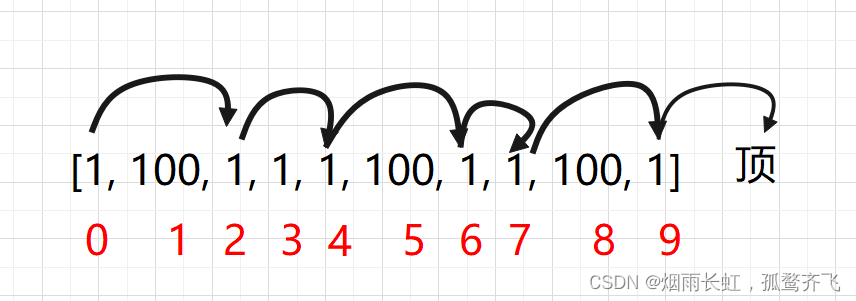
输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 输出:6 解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
思路:
由题意可知:我们的楼层顶部并不是数组的末元素,而是末元素的下一位
<1>状态表示 以 i 为结尾,dp[i]表示到达 i 位置时,最小花费 <2>状态转移方程 使用之前或者之后的状态,推导出dp[i]的值
根据最近的一步来划分问题
(1)先到达 i-1 的位置,然后支付cost[i-1],走一步:dp[i-1]+cost[i-1]
(2)先到达 i-2 的位置,然后支付cost[i-2],走二步:dp[i-2]+cost[i-2]
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
<3>初始化 由题意 你可以选择从下标为 0 或 1 的元素作为初始阶梯 得:
dp[0] = dp[1] = 0
<4>填表顺序 从左往右 <5>返回值 dp[n]
代码测试:
class Solution { public:int minCostClimbingStairs(vector<int>& cost) {//计算数组长度int n = cost.size();vector<int> dp(n+1);//初始化dp[0] = dp[1] = 0;//顺序填表for(int i = 2;i<=n;i++)//状态转移方程dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);return dp[n]; } };
路径问题
数字三角形
题目链接:数字三角形
题目描述#
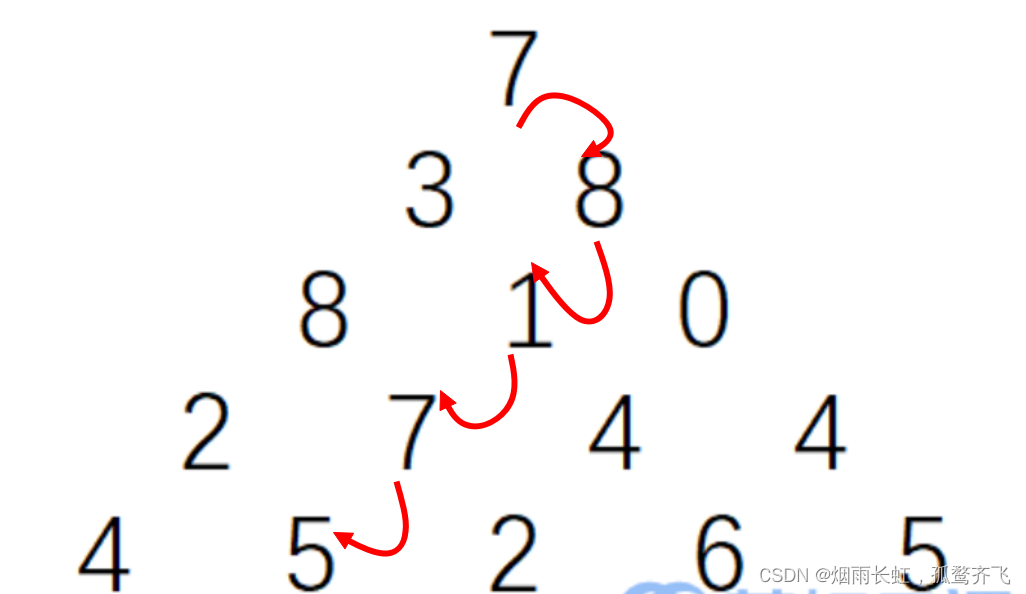
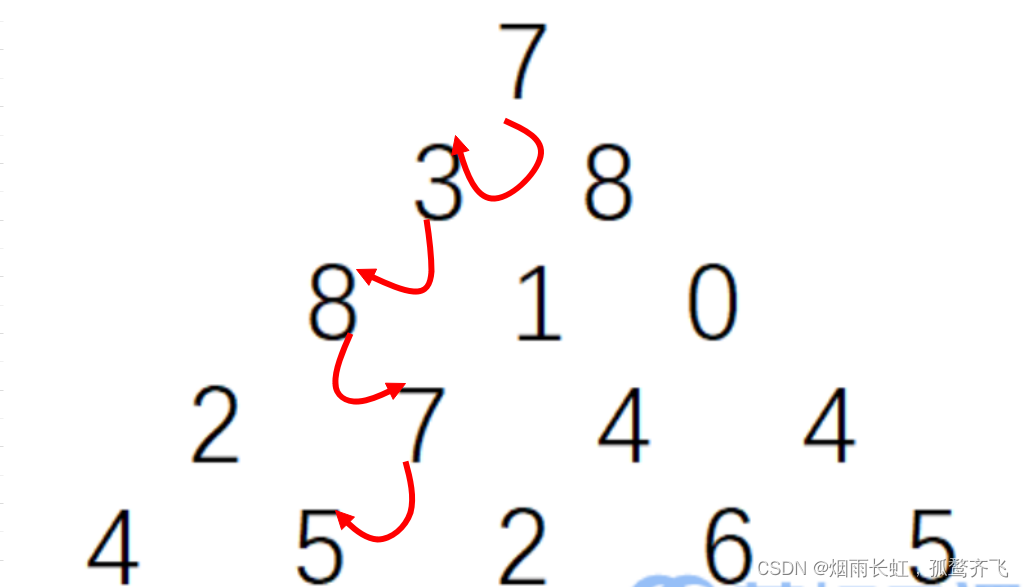
观察下面的数字金字塔
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
在上面的样例中,从 7→3→8→7→5 的路径产生了最大权值。
输入格式#
第一个行一个正整数 r 表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式#
单独的一行,包含那个可能得到的最大的和。
输入输出样例#
输入 #1
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5输出 #1
30
思路:
在看到数字三角形的构造时,我们首先想到用 二维数组 来存放整个三角形(行与列)
也许有人会想到 贪心算法 来实现,但是贪心算法在这里是不适用的
贪心只注重眼前的利益(如上图),贪心策略算出的数字的和是:28 不符合我们的最大值
所以眼光放长,我们要的是最后的数字和最大,尝试用 动态规划 解决问题
注意:
我们发现从上面往下一步步走很麻烦,直接搜索肯定超时
所以我们的切入点是 由下至上 的回溯,依层次更换改动大值,回到顶端时,就是结果
例如:
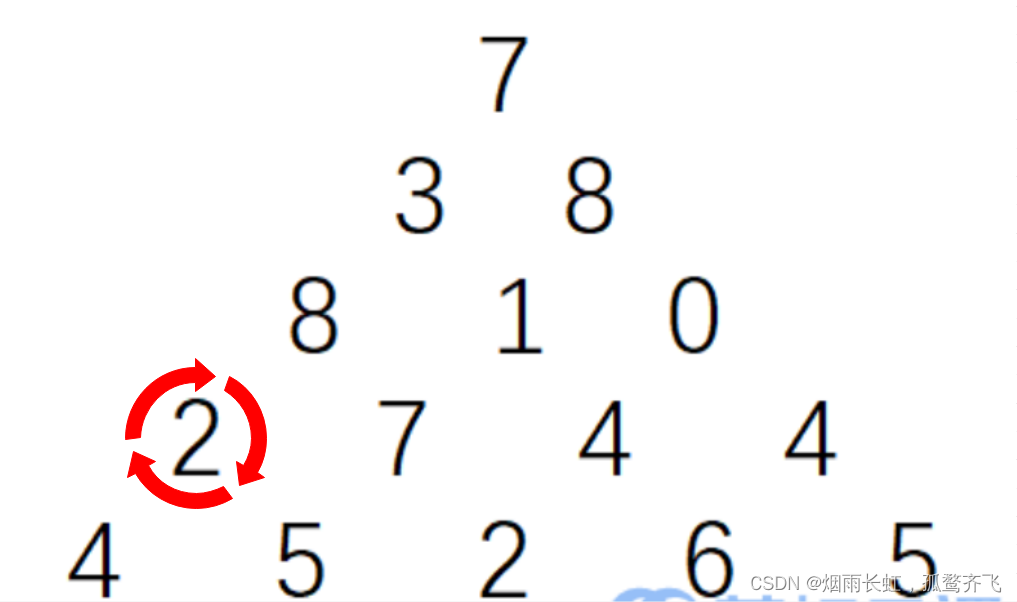
我们找到倒数第二排的元素 2 ,此时只有两种方法可以走,左下方或者右下方
我们要保证数字和最大,所以必然选择 右下方 ,这个时候的较大值为 7
同理:我们考虑倒数第二排的元素 7 ,较大值为 12
依次类推则倒数第二排变为:
7 12 10 10因为我们的倒数第二排已经包含了最后一排的最优解,所以我们的三角形可以简化成:
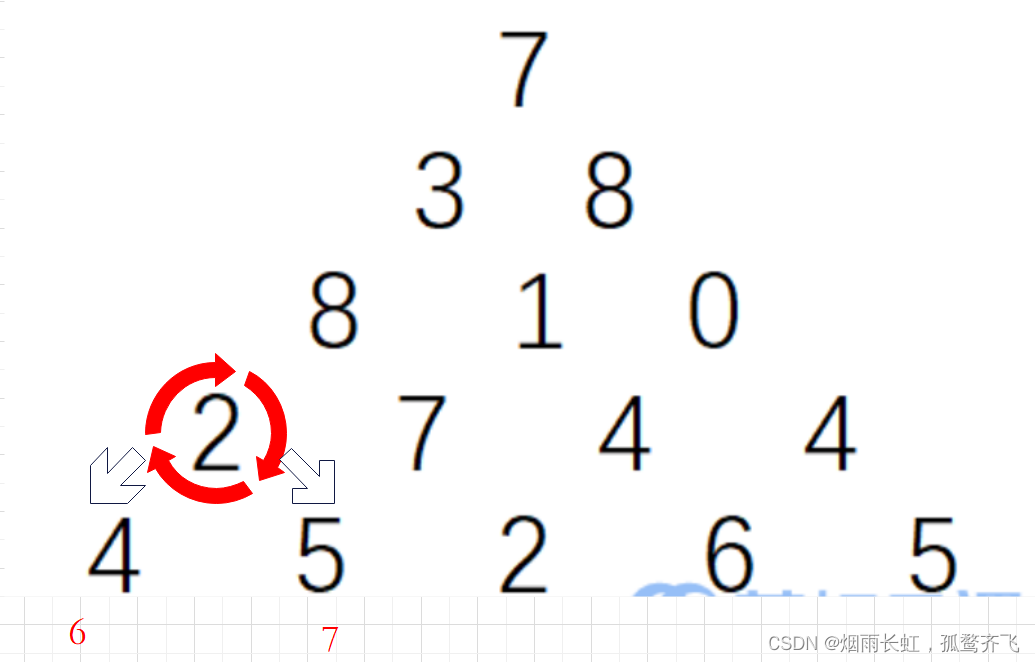
7 3 8 8 1 0 7 12 10 10方法同上我们找到倒数第二排的元素 8 ,再比较走两条路的值,右边的值更大,选择右边的值,所以这个时候的较大值为 20
以此类推,得到下面的数字三角形:
7 3 8 20 13 107 23 2130 23 21 20 13 10 7 12 10 10 4 5 2 6 5最后得到我们的最大数字之和为 30
所以我们的最佳路径是:7→3→8→7→5
思路我们已经理清了,接下来开始推导我们的状态转移方程:
<1>状态表示 以 [i,j] 为结尾,dp[ i ][ j ]表示到达 [i,j] 位置时,最大的数字之和 <2>状态转移方程 dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1])
<3>初始化 按要求输入
<4>填表顺序 从下至上,从左至右 <5>返回值 dp[1][1] <6>小总结 画图求解,发现规律,列出状态转移方程
代码测试:
#include<bits/stdc++.h> using namespace std; int main() {int n = 0;cin>>n;vector<vector<int>> dp((n+1),vector<int>(n+1));//初始化for(int i = 1;i<=n;i++)for(int j = 1;j<=i;j++)cin>>dp[i][j];//顺序填表for(int i = n-1;i>=1;i--)for(int j = 1;j<=i;j++)//状态转移方程dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1]);//返回值cout<<dp[1][1]<<endl;return 0; }
不同路径
题目链接:不同的路径
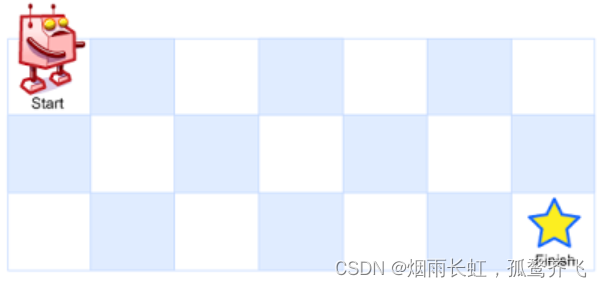
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角
(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28示例 4:
输入:m = 3, n = 3 输出:6提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 10^9
思路:
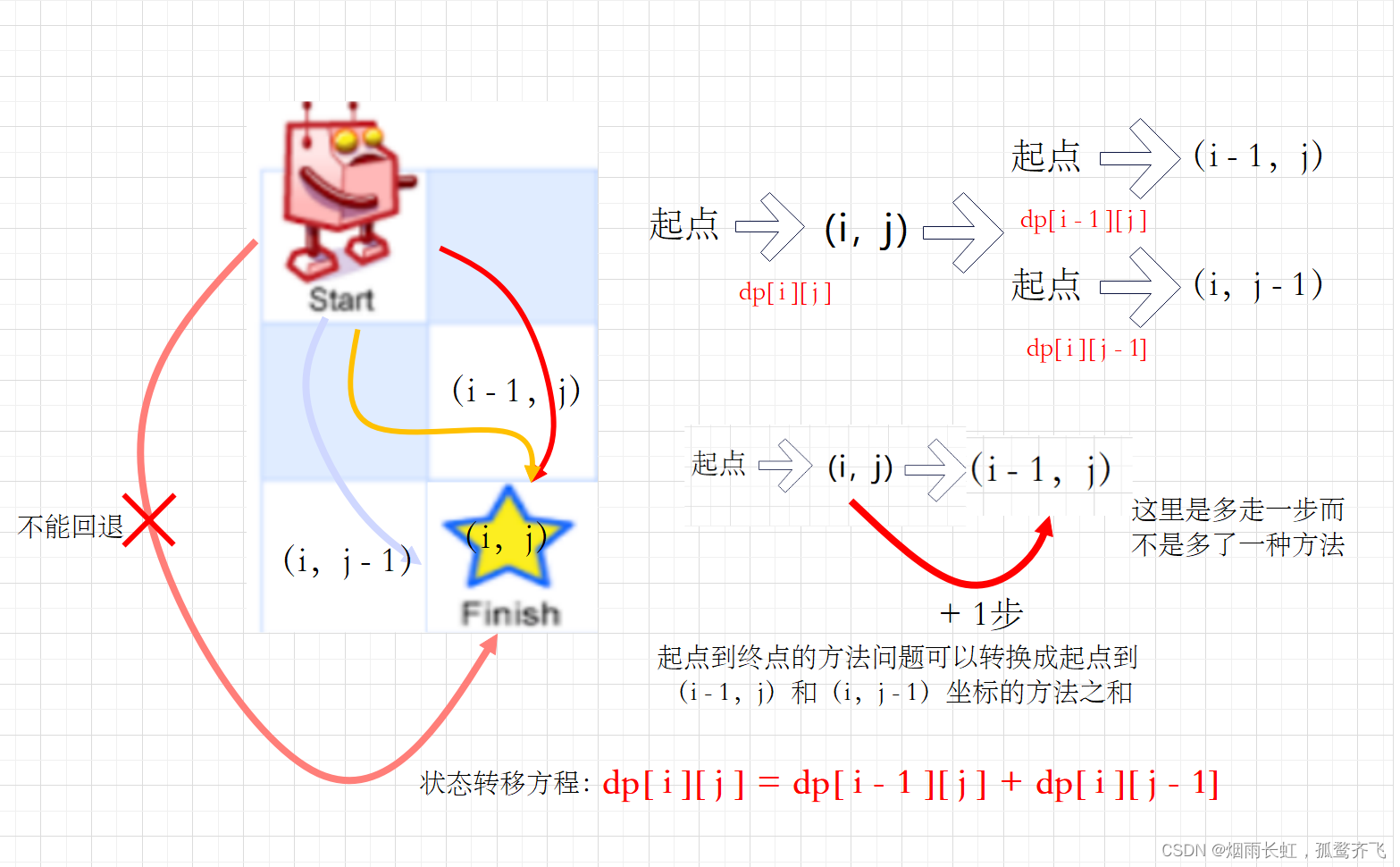
二维dp
状态转移方程的得出
初始化问题
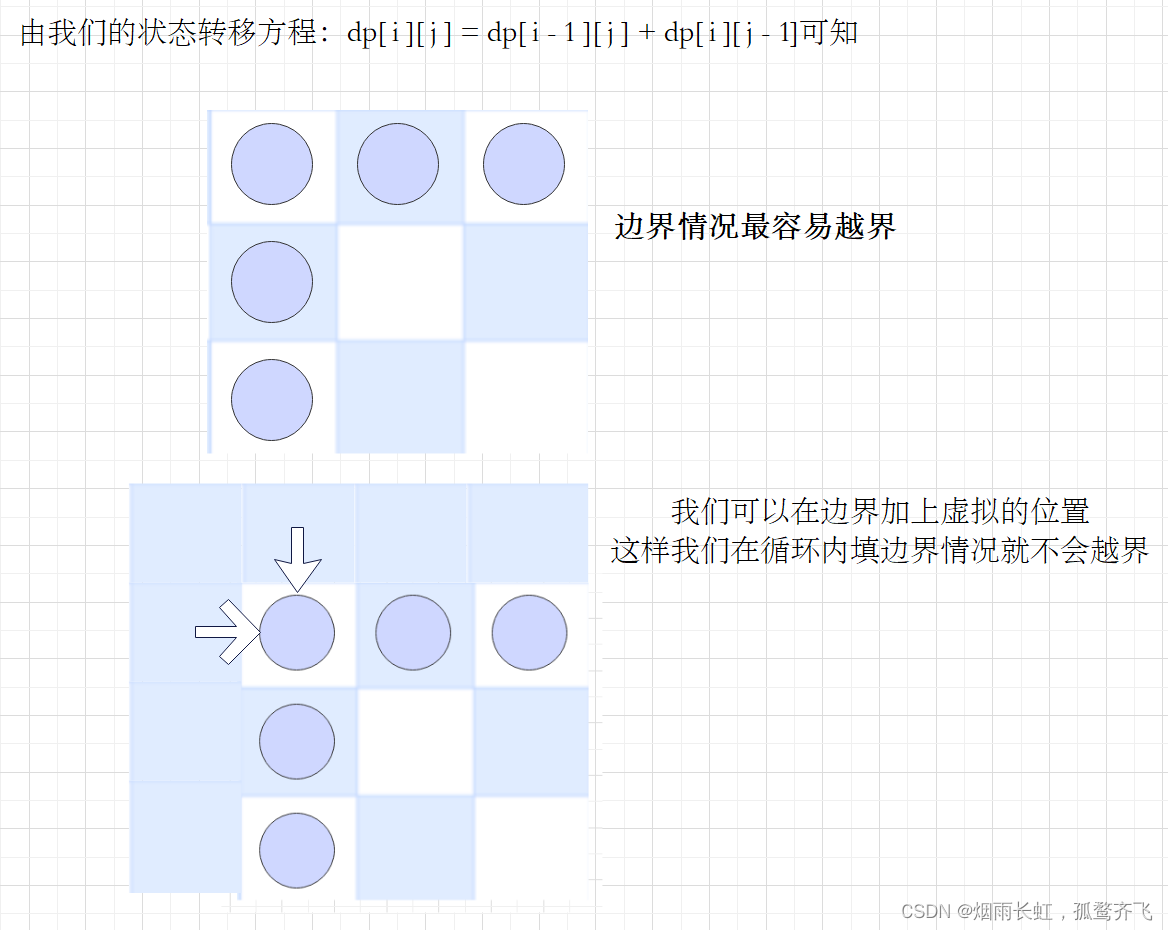
为了防止数组越界,所以我们要考虑 dp 的初始化问题
注意:
<1>然后在考虑虚拟位置的值,要保证我们后面填表的结果是正确的
<2>二维数组的行和列都要加一(加上了虚拟位置)
我们只要将 dp[0][1] 或者 dp[0][1] 的位置初始化为 1 就可以了
<1>状态表示 以[i,j]为结尾时,dp[i][j]表示走到[i,j]的位置,一共有多少种方式 <2>状态转移方程 dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i ][ j - 1]
<3>初始化 dp[0][1] = 1 <4>填表顺序 从左至右,从上至下 <5>返回值 dp[m][n] 代码测试:
class Solution { public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1));//初始化dp[0][1] = 1;//顺序填表for(int i = 1;i<=m;i++)for(int j = 1;j<=n;j++)//状态转移方程dp[i][j] = dp[i-1][j]+ dp[i][j-1];//返回值return dp[m][n];} };
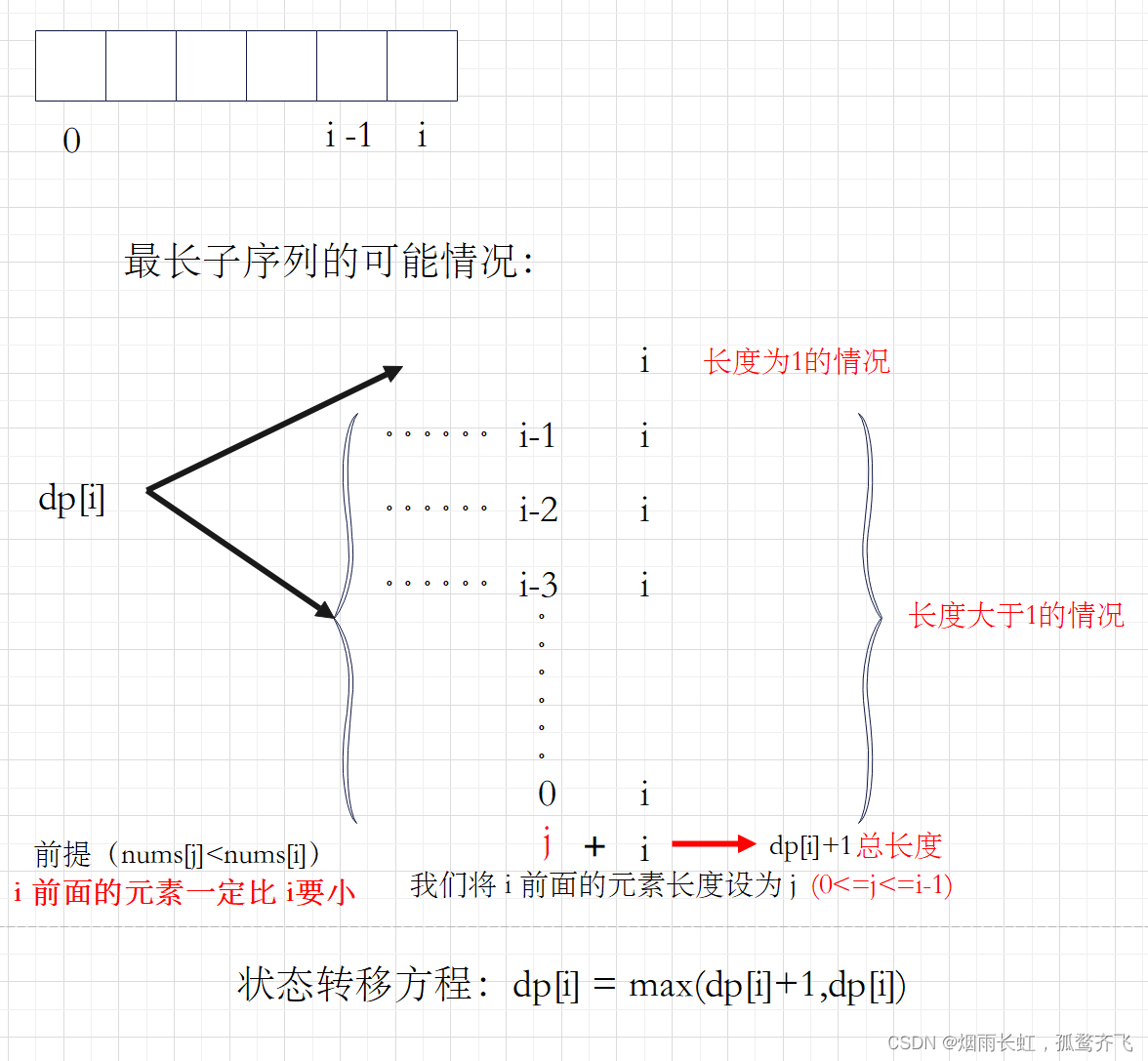
LIS模型
最长递增子序列
题目链接:最长递增子序列
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
思路:
子序列的介绍:
子序列指的是一个序列中,按照原顺序选出若干个 一定连续 的元素所组成的序列
状态转移方程的推理:
初始化:将dp标准的状态成最坏的情况,最后更新dp表就可以了
填表顺序:因为我们要填 dp[i] 就要用到前面的值,所以是:从左往右
注意:要判断 nums[j]<nums[i]
<1>状态表示 dp[i]表示以 i 位置为结尾的所有子序列中,最长递增子序列的长度 <2>状态转移方程 dp[i] = max(dp[i]+1,dp[i])
<3>初始化 dp表中所有元素都置为1 <4>填表顺序 从左往右 <5>返回值 dp表中的最大值 代码测试:
class Solution { public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();//初始化vector<int> dp(n,1);int ret = 1;//顺序填表for(int i = 1;i<n;i++){for(int j = 0;j<i;j++)//前提条件if(nums[j]<nums[i])//状态转移方程dp[i] = max(dp[j]+1,dp[i]);ret = max(ret,dp[i]);}//返回值return ret;} };