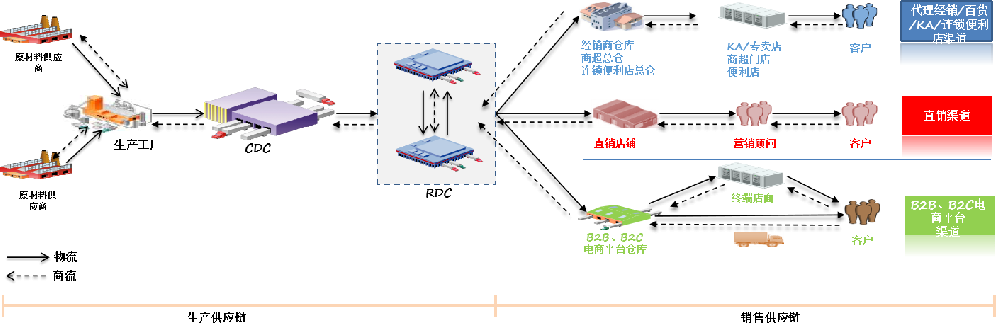
实现典型数据结构的查找、添加和删除数据 并分析其时间和空间复杂度

• 线性结构：

数组：是一种线性表数据结构，它用一组连续的内存空间，来存储一组具有相同类型的数据。

1. 查找数据 ：随机访问

• 流程图

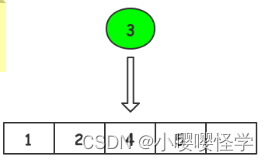
/**  查询元素下标*  参数1：Array_t数组结构体指针*  参数2：元素值*  返回：成功返回元素下标，失败返回-1*/
int search(struct Array_t *array, int elem){int idx = 0;// 遍历数组for (idx = 0; idx < array->used; idx++){// 找到与查询的元素值相同的数组元素，则返回元素下标if (array->arr[idx] == elem){return idx;}// 如果数组元素大于新元素，说明未找到此数组下标, 则提前报错退出// 因为本例子的数组是有序从小到大的if (array->arr[idx] > elem){break;}}// 遍历完，说明未找到此数组下标，则报错退出std::cout << "ERROR: No search to this" << elem << " elem." << std::endl;return -1;
}

• 复杂度分析（时间和空间）

时间复杂度：已知索引 O(1)；未知索引 O(n)；

空间复杂度：O(n)。

---

2.添加数据

• 流程图

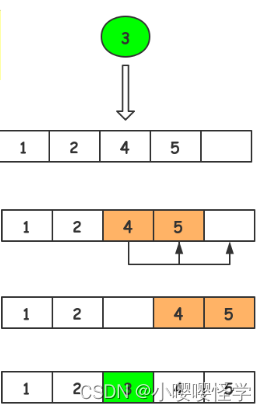
/**  插入新元素*  参数1：Array_t数组结构体指针*  参数2：新元素的值*  返回：成功返回插入的数组下标，失败返回-1*/
int insertElem(struct Array_t *array, int elem){// 当数组被占用数大于等于数组长度时，说明数组所有下标都已存放数据了，无法在进行插入if (array->used >= array->length){std::cout << "ERROR: array size is full, can't insert " << elem << " elem." << std::endl;return -1;}int idx = 0;// 遍历数组，找到大于新元素elem的下标idxfor (idx = 0; idx < array->used; idx++){// 如果找到数组元素的值大于新元素elem的值，则退出if (array->arr[idx] > elem){break;}}// 如果插入的下标的位置不是在末尾，则需要把idx之后的// 数据依次往后搬移一位，空出下标为idx的元素待后续插入if (idx < array->used){// 将idx之后的数据依次往后搬移一位memmove(&array->arr[idx + 1], &array->arr[idx], (array->used - idx) * sizeof(int));}// 插入元素array->arr[idx] = elem;// 被占用数自增array->used++;// 成功返回插入的数组下标return idx;
}

• 复杂度分析）

时间复杂度：未知索引 O(n)；

空间复杂度：O(n)。

• 可以改进

我们的数组是无序的，插入一个元素也不在乎顺序，也没有指定插入元素的位置，那么这时候就可以选择直接插入尾部；如果插入元素时指定了一个插入位置，如果不关心顺序的话也可以采用一种巧妙的办法来实现：

public static void addByElement(int[] arr, int size, int index,int element) {if (null == arr || arr.length == 0){//数组是否为空return;}if (size >= arr.length){//确认数组至少有一个空位return;}arr[size] = arr[index];//将 index 和有效数组位数的最后一位交换arr[index] = element;

这里其实就是直接将需要插入元素的位置上的原有元素放到最后，然后再直接插入，避免了数组的移动，实现了 O(1) 时间复杂度的插入。

---

3.删除数据

• 流程图

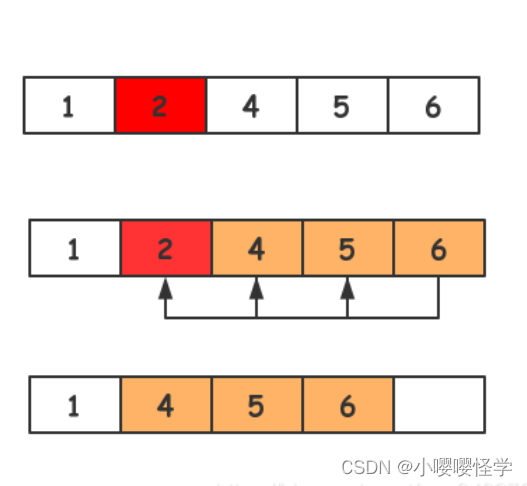
/**  删除新元素*  参数1：Array_t数组结构体指针*  参数2：删除元素的数组下标位置*  返回：成功返回0，失败返回-1*/
int deleteElem(struct Array_t *array, int idx){// 判断下标位置是否合法if (idx < 0 || idx >= array->used){std::cout << "ERROR:idx[" << idx << "] not in the range of arrays." << std::endl;return -1;}// 将idx下标之后的数据往前搬移一位memmove(&array->arr[idx], &array->arr[idx + 1], (array->used - idx - 1) * sizeof(int));// 数组占用个数减1array->used--;return 0;
}

• 复杂度分析

时间复杂度：O(n)；

空间复杂度：O(n)。