​"Strive not to be a success, but rather to be of value." 

- Albert Einstein

1. 题目描述

2.  题目分析与解析

2.1 暴力求解

没思路，老规矩，先来一次笨办法，先把步子迈出去，因为可能笨办法写着写着就会有更多的理解，从而产生新的思路。这个题目暴力求解还是挺容易理解的，就是看每一行，每一列，以及每个粗线包括的3×3方框是否有重复的1-9的数字，出现直接返回false，都没出现返回true。

代码思路：

• 一次for遍历每一行

• 一次for遍历每一列

• 一次for遍历每个3×3方块

• 使用一个9个元素的数组记录出现的次数当，某一个数字出现不止一次返回false。

但是运行之后没想到效果还挺好：

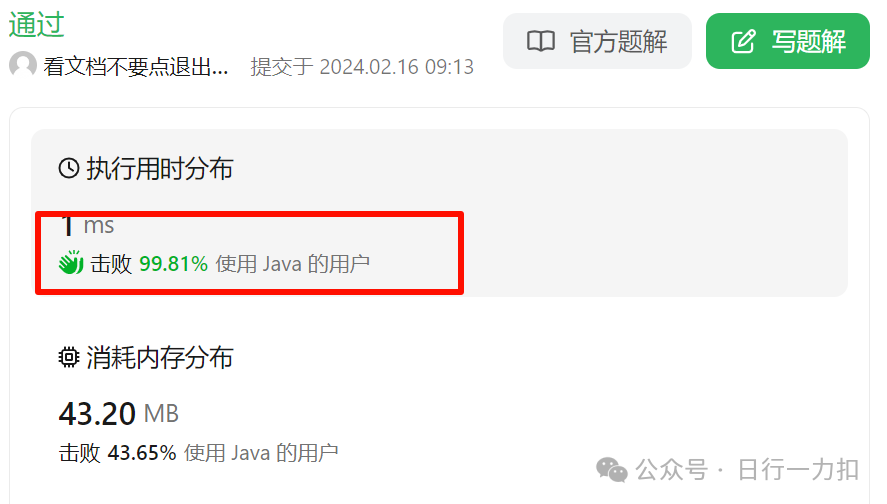
然后我开始也很震惊，明明这种暴力求解的方法看起来很复杂，但是我又思考了一下，想到为什么能获得这样的效果，就是其实我只进行了三次遍历所有元素的操作，因为矩阵是N×N的，实际上虽然遍历矩阵的时间复杂度是O(N^2)，但是只进行了三次遍历，也就是O(3*N^2)，复杂度最终是O(N^2)。

2.2 思路二——优化

现在思考一下，本质上我们的暴力求解其实就是寻找数组中每一个元素对于当前行或者当前列，或者当前3×3的小方块的影响，那我们是不是可以把每一个位置对于这三种情况的影响存储起来，就不需要每一次针对一种情况去重新看它在该种情况下造成的影响呢？

答案是可以的，由于我们在遍历board数组的任意一个位置，其实我们是可以将该位置对于其所在行，所在列以及3×3小方块先存储起来的，这样就可以一次性遍历所有二维数组元素同时判定结果。实际上就是空间换时间。

空间换时间的本质：其实就是开辟额外的空间，将我已经走过的地方的需要的信息尽可能存储起来，减少回过头去收集信息的开销。

代码思路：

• 两层for循环是肯定的，因为要遍历所有元素

• 对于每一行，使用一个数组记录，一共9个Boolean 数组

• 对于每一列，使用一个数组记录，一共9个Boolean 数组

• 对于3×3的小方块，总共可以看出有9个3×3小方块，所以也使用9个Boolean 数组

• 对于每一个遍历到的元素，首先判断它对应的行的影响，将它对所在列以及3×3方块的影响存储起来：

  • 如果对应的位置是false，表示先前没有元素，置为true。

  • 如果为true，则表示有重复元素，返回false

3. 代码实现

3.1 暴力求解

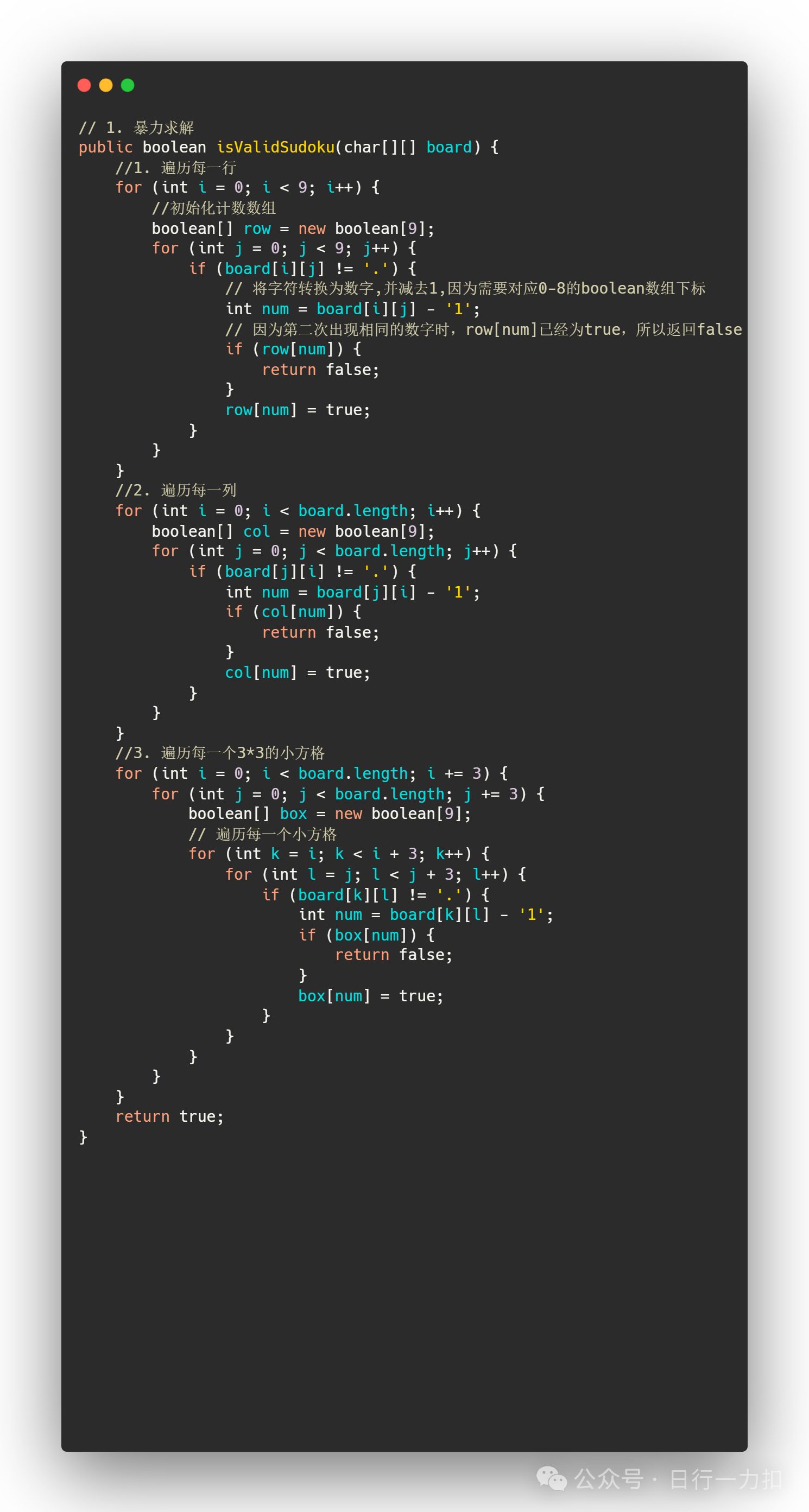
3.2 优化

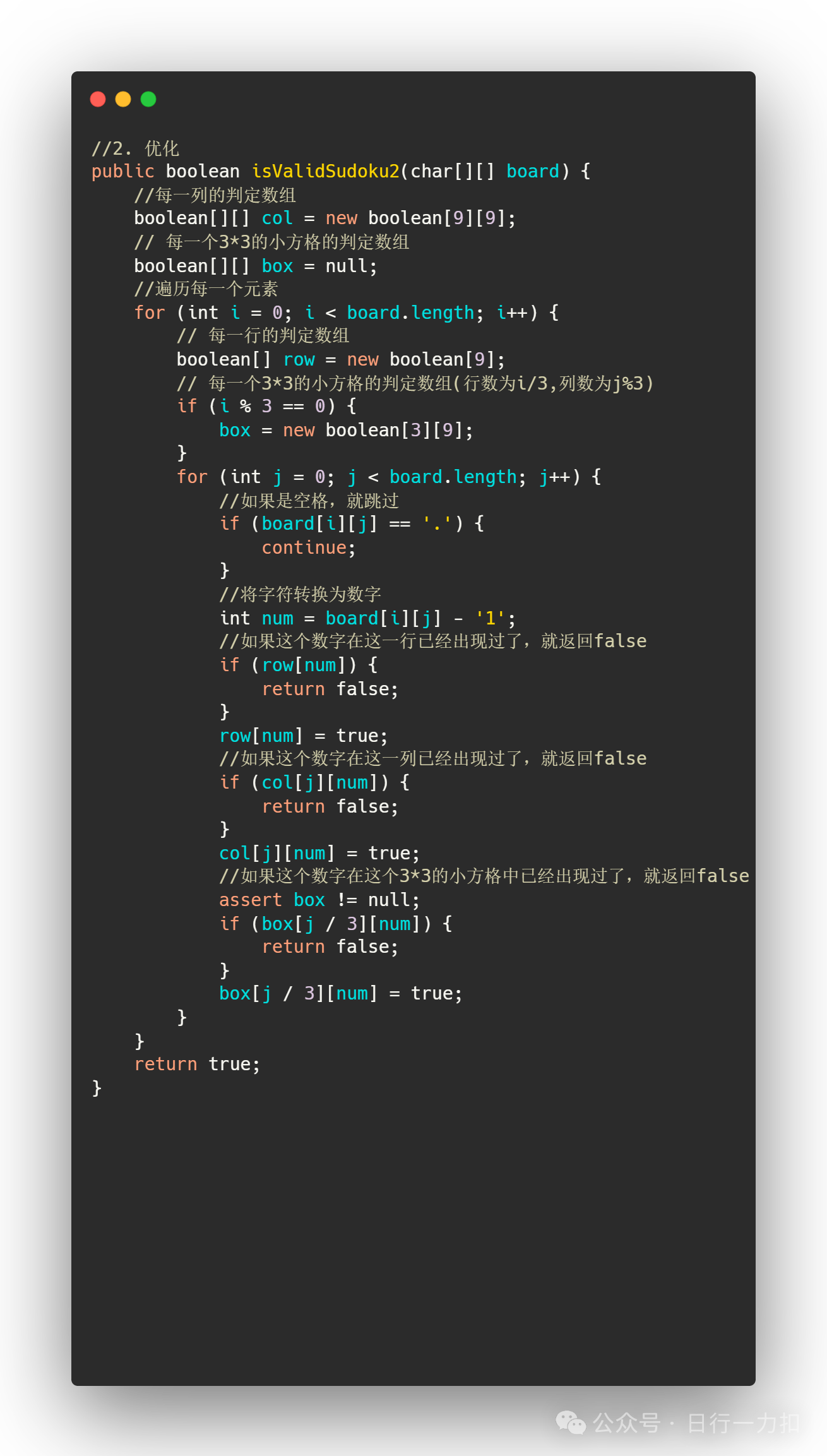
之所以运行效果差别不大就是因为二者的复杂度都是O(N^2)，只不过暴力解法遍历了三次，优化方法只遍历了一次，而且矩阵也比较小，所以运行效果差异不明显。

4. 相关复杂度分析

4.1 暴力求解

时间复杂度

• 遍历每一行：对于每行，都要检查9个元素是否满足数独的条件，因此时间复杂度为O(9x9)。

• 遍历每一列：同样地，需要遍历每列的9个元素，时间复杂度为O(9x9)。

• 遍历每一个3x3的小方格：总共有9个小方格，每个小方格内部再进行9次操作来检查元素，时间复杂度为O(9x9)。

总的来说，每个单独的步骤都是对81个单元格进行操作，所以总时间复杂度为O(3x9x9)，简化后仍然是O(9x9)。

空间复杂度

• 对于每一行、每一列、每个3x3的小方格，都有一个单独的布尔数组来记录数字是否出现过，这个数组的大小是9。

• 因为这些数组是在遍历过程中被创建，并在每次遍历开始时重新初始化，所以它们不会同时存在。

总的空间复杂度为O(9)，即在任何时刻，最多有一个长度为9的布尔数组在使用中。

4.2 优化

时间复杂度

• 这个方法通过一次遍历来检查行、列、和3x3的小方格的有效性。对于每个元素，进行一系列的检查（包括行、列、小方格），每次检查的时间复杂度都是O(1)。

• 总体上，需要遍历整个9x9的数独板一次，所以时间复杂度为O(9x9)。

空间复杂度

• 使用了三个二维布尔数组来分别记录列、行和3x3小方格内数字是否已经出现过。每个数组的大小为9x9。

• col数组用于记录每一列数字是否出现过，row数组在每次行的遍历开始时初始化，而box数组的处理稍微复杂一些，但本质上是对每个小方格进行跟踪。

总的空间复杂度为O(9x9) + O(9x9) + O(3x9)，即主要由三个二维数组的大小决定，可以简化为O(9x9)。在第二种解法中，尽管box数组在逻辑上是一个3x9的数组，但实际上为了简化索引计算和逻辑处理，通常会使用9x9的数组来表示所有的小方格，因此这里按照最终实现可能占用的空间来估算。

4.3 结论

• 时间复杂度方面，两种方法都是O(9x9)，因为它们都需要遍历整个数独板。

• 空间复杂度方面，第一种方法为O(9)，因为它在任何时刻最多使用一个大小为9的布尔数组。第二种方法的空间复杂度提高到了O(9x9)，因为它同时使用了多个二维数组来跟踪行、列和3x3小方格中数字的出现情况，但是如果对于很大的矩阵来讲，第二种方法会更好，因为它只需要遍历一次整个数组，而第一种方法需要遍历三次。