并查集是简单的数据结构,学会并查集,为图打好基础。
并查集的概念
是树状的数据结构,用于处理相交集合的合并与查询
通常用森林表示,一片森林表示一个集合
并查集一般需要完成
- 查找元素属于哪个集合
- 查看两个元素是否属于同一个集合
- 将两个集合归并成一个集合
- 集合的个数
并查集的原理
假设有10个人,用集合表示为{0,1,2,3,4,5,6,7,8,9}
我们用数组表示这十个人
- 数组的下标表示人的编号
- 数组的内容表示每个人认识其中人的数目 (-1 表示只认识自己)
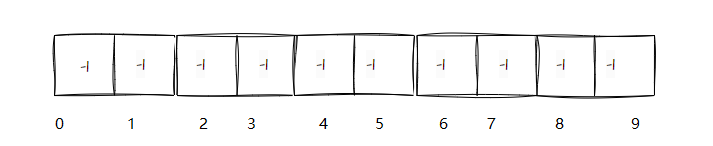
表示为10片森林
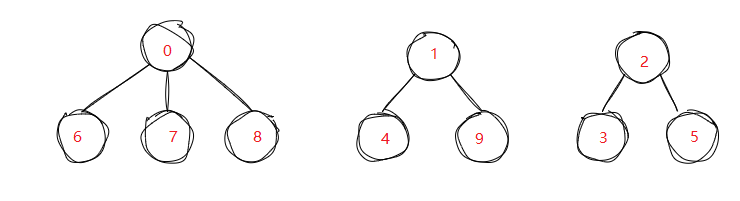
经过一段时间后,他们形成三个小团体,s1{0,6,7,8} s2{1,4,9} s3{ 2,3,5}
利用并查集表示
- 数组的下标对应集合中元素的编号
- 数组中如果为负数,负号代表根,数字代表该集合中元素个数
- 数组中如果为非负数,代表该元素双亲在数组中的下标

所以在并查集中,我们会关注数组的下标和数组的内容。
如果数组的内容是负数,那么他就是根(Root)
如果数组的内容为(非负数),那么就指向他的父亲。
所以我们能简单解决这些问题
- 查找元素属于哪个集合
沿着树形关系一直往上寻找到根(直到找到内容为负数的)
- 查看元素是否属于同一个集合
寻找到根,不同则表示不是同一个集合
- 将两个集合归并成一个集合
一个集合归并到另一个集合中,并修改集合的内容
- 集合的个数
多少个负数内容的位置,就有多少个集合
接下来,来简单实现一个并查集
并查集的模拟
框架
//并查集
class UnionFindSet {
public://构造函数UnionFindSet(int n);//查找元素所在的集合int findRoot(int x);//合并两个元素所在的集合void Union(int x1, int x2)//获取并查集中集合的个数int SetCount();
private:vector<int> _set;各个结点之间的关系
};
构造
接收vector容器应该预留的空间
初始化为-1
UnionFindSet(int size):_set(size,-1){}不需要自定析构函数
默认会调用系统默认析构
查找root
一直向上寻找,变换x ,直到找到内容为负数
//查找元素是否在集合里size_t FindRoot(int x){while (_set[x] >= 0){x = _set[x];}return x;}合并俩个集合
将B合并到A中,A的根内容要改变,B的根内容也要改变
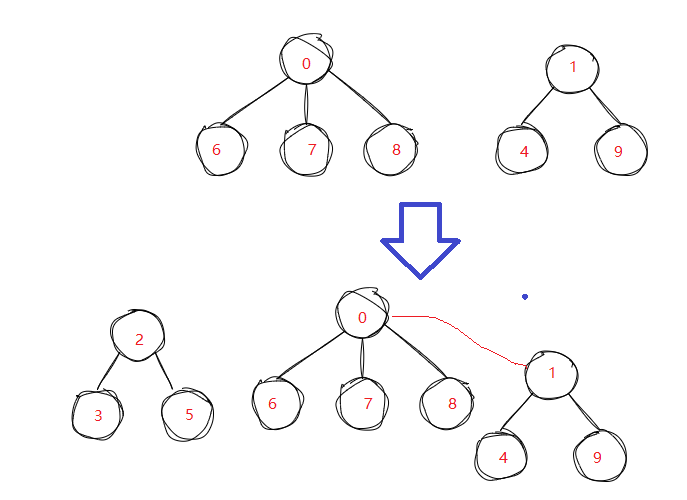
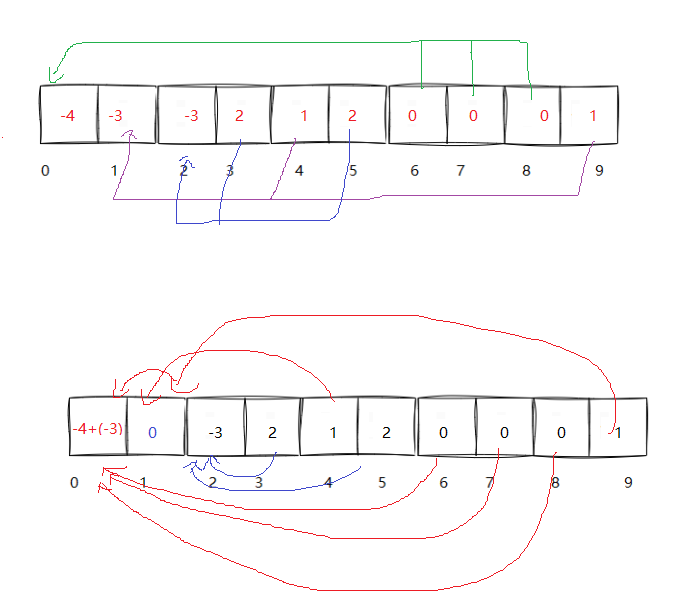
//合并void Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 != root2){_set[root1] += _set[root2];_set[root2] = root1; }}路径压缩
如果有大量的数据,那么树的层数可能非常高,查找的时候就需要一层一层往上迭代。这时候很浪费效率,这里就提出路径压缩。
路径压缩一般发送在查找根结点,会压缩路径上的所有结点,挂接到根上。

size_t FindRoot(int x){//找根size_t root = x;while (_set[x] >= 0){x = _set[x];}//压缩while (_set[x] >= 0){size_t parent = _set[x];_set[x] = root;x = parent;}return root;}Gitee:提取代码
相关题目
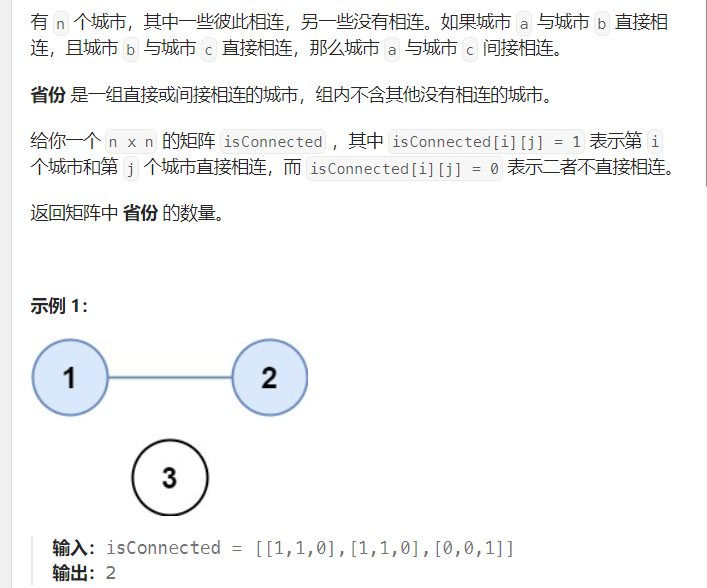
LCR 116. 省份数量
思路:
运用并查集的相关知识
题目给我们一个相邻矩阵,遍历一半矩阵就能知道连通的关系。
我们把矩阵中为1的放到一个集合中,返回集合的数目
解题时,运用lambda表达式,调用找根root的函数。
class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {int n=isConnected[0].size();vector<int> _ufs(n,-1);//找根 >=0 就往上找auto FindRoot=[&_ufs](int x){int parent=x;while(_ufs[parent]>=0){parent=_ufs[parent];}return parent;};//遍历,遇到1 并且根不同 就合并 for(int i=0;i<n;i++){for(int j=0;j<=i;j++){if(isConnected[i][j]==1){int root1=FindRoot(i);int root2=FindRoot(j);if(root1!=root2){_ufs[root1]+=_ufs[root2];_ufs[root2]=root1;}}}}int count =0;for(auto x:_ufs){if(x<0)count++;}return count;}
};