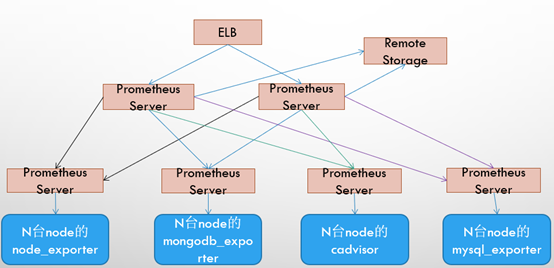
随着人工智能、大数据等技术的飞速发展，数学工具的重要性日益凸显。向量内外积作为线性代数中的基础概念，不仅在理论上有着深远的影响，在实际应用中也发挥着巨大作用。本文将从向量内外积的定义、起源、应用场景以及计算示例等方面，为您详细解读这一数学概念。

一、向量内外积是什么？

向量内外积，又称点积或标量积，是指两个向量在某一方向上的投影长度乘积。数学上，设有两个向量a和b，它们的点积定义为：a·b = |a||b|cosθ，其中|a|和|b|分别表示向量a和b的长度，θ表示向量a和b之间的夹角。

二、向量内外积的起源

向量内外积的概念最早可以追溯到19世纪，由德国数学家奥古斯丁·路易·柯西提出。柯西通过研究向量之间的运算规律，提出了点积的定义，为后来线性代数的发展奠定了基础。

三、向量内外积有什么用？

向量内外积在理论研究和实际应用中有着广泛的应用场景。以下简要介绍几个典型应用：

1. 计算向量的投影长度：向量内外积可以方便地计算出向量在一个方向上的投影长度，这在几何、物理等领域具有重要意义。

2. 判断向量垂直关系：当两个向量的点积为0时，它们在三维空间中垂直。这一性质在工程设计和计算机图形学等领域有着广泛的应用。

3. 计算矩阵的行列式：向量内外积与矩阵的行列式密切相关，通过点积可以推导出矩阵行列式的计算方法。

4. 机器学习：在机器学习中，向量内外积常用于计算相似度，如余弦相似度等。此外，点积在神经网络中的权重更新也有重要应用。

四、向量内外积计算示例

假设有两个三维空间中的向量a和b，分别为：

a = (1, 2, 3)

b = (4, 5, 6)

首先计算向量a和b的长度：

|a| = √(1^2 + 2^2 + 3^2) = √14

|b| = √(4^2 + 5^2 + 6^2) = √77

接着计算向量a和b之间的夹角cosθ：

cosθ = (1×4 + 2×5 + 3×6) / (√14×√77) = 32 / (11.66×8.77) ≈ 0.4

最后计算向量a和b的点积：

a·b = |a||b|cosθ = √14×√77×0.4 ≈ 32

综上所述，向量内外积作为一种基础的数学工具，不仅在理论上具有深远影响，而且在实际应用中发挥着重要作用。掌握向量内外积的计算方法及其应用场景，将有助于我们更好地解决实际问题，为科技发展助力。

——微信搜索【数学思维计算器】使用向量计算器