本文为Python算法题集之一的代码示例

题230：二叉搜索树中第K小的元素

1. 示例说明

• 给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

  示例 1：

  

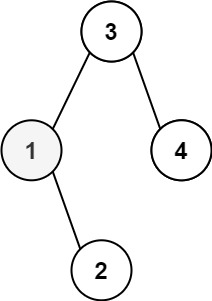
  输入：root = [3,1,4,null,2], k = 1
  输出：1
  

  示例 2：

  

  输入：root = [5,3,6,2,4,null,null,1], k = 3
  输出：3
  

  提示：

  • 树中的节点数为 n 。
  • 1 <= k <= n <= 104
  • 0 <= Node.val <= 104

  **进阶：**如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

---

2. 题目解析

- 题意分解

1. 本题为在二叉搜索树中寻找第K小的值
2. 基本的基本思路是深度优先算法【DFS（Depth-First Search）】、广度有限算法【BFS（Breadth-First Search）】

- 优化思路

1. 通常优化：减少循环层次

2. 通常优化：增加分支，减少计算集

3. 通常优化：采用内置算法来提升计算速度

4. 分析题目特点，分析最优解

   1. 通过DFS、BFS进行中序遍历，找到第K个值

   2. 可以测试高速双向队列deque的性能

---

- 测量工具

• 本地化测试说明：LeetCode网站测试运行时数据波动很大，因此需要本地化测试解决这个问题
• CheckFuncPerf（本地化函数用时和内存占用测试模块）已上传到CSDN，地址：Python算法题集_检测函数用时和内存占用的模块
• 本题本地化超时测试用例自己生成，详见【最优算法章节】

---

3. 代码展开

1) 标准求解【DFS递归+终止检测】

使用DFS递归中序遍历求解，找到第K个值后返回

马马虎虎，超过64%

import CheckFuncPerf as cfpclass Solution:def kthSmallest_base(self, root, k):def inOrder_findk(root, result, k):if root == None:returnif inOrder_findk(root.left, result, k):return Trueresult.append(root.val)if len(result) == k:return Trueif inOrder_findk(root.right, result, k):return Truereturn Falseresult = []inOrder_findk(root, result, k)return result[-1]aroot = sortedArrayToBST(nums)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.kthSmallest_base, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 运行结果
函数 kthSmallest_base 的运行时间为 11.97 ms；内存使用量为 756.00 KB 执行结果 = 50999

2) 改进版一【BFS迭代+终止检测】

使用BFS迭代中序遍历求解，找到第K个值后返回

天下无双，超越99%

import CheckFuncPerf as cfpclass Solution:def kthSmallest_ext1(self, root, k):stack, result, iPos = [], [], kwhile root or stack:if root:stack.append(root)root = root.leftelse:curnode = stack.pop()iPos -= 1if iPos == 0:return curnode.valresult.append(curnode.val)root = curnode.rightaroot = sortedArrayToBST(nums)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.kthSmallest_ext1, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 运行结果
函数 kthSmallest_ext1 的运行时间为 9.97 ms；内存使用量为 0.00 KB 执行结果 = 50999

3) 改进版二【BFS迭代+终止检测+计数定位】

使用BFS迭代中序遍历求解，直接通过计数定位获取节点值【不生成中序遍历结果】

性能优越，超过91%

import CheckFuncPerf as cfpclass Solution:def kthSmallest_ext2(self, root, k):stack = [root]while stack:curnode = stack.pop()while curnode:stack.append(curnode)curnode = curnode.leftcurnode = stack.pop()k-=1if k==0:return curnode.valstack.append(curnode.right)aroot = sortedArrayToBST(nums)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.kthSmallest_ext2, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 运行结果
函数 kthSmallest_ext2 的运行时间为 8.98 ms；内存使用量为 0.00 KB 执行结果 = 50999

4) 改进版三【BFS迭代+终止检测+计数定位+高速双向队列】

使用BFS迭代中序遍历求解，采用高速双向队列deque替换list，直接通过计数定位获取节点值【不生成中序遍历结果】

性能优良，超过83%

import CheckFuncPerf as cfpclass Solution:def kthSmallest_ext3(self, root, k):from collections import dequestack = deque([root])while stack:curnode = stack.pop()while curnode:stack.append(curnode)curnode = curnode.leftcurnode = stack.pop()k-=1if k==0:return curnode.valstack.append(curnode.right)aroot = sortedArrayToBST(nums)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.kthSmallest_base, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 运行结果
函数 kthSmallest_ext3 的运行时间为 8.98 ms；内存使用量为 8.00 KB 执行结果 = 50999

---

4. 最优算法

根据本地日志分析，本次出现了并列的最优算法，第3种方式【BFS迭代+终止检测+计数定位】、第4种方式【BFS迭代+终止检测+计数定位+高速双向队列】kthSmallest_ext2、kthSmallest_ext3速度一致，说明list、deque在某些操作上是基本等价的

iLen = 5000000
nums = [x for x in range(iLen)]
def sortedArrayToBST(nums):if not nums:returnmid = len(nums) // 2root = TreeNode(nums[mid])if mid == 0:return rootroot.left = sortedArrayToBST(nums[:mid])root.right = sortedArrayToBST(nums[mid+1:])return root
aroot = sortedArrayToBST(nums)
aSolution = Solution()
result = cfp.getTimeMemoryStr(Solution.kthSmallest_base, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))
result = cfp.getTimeMemoryStr(Solution.kthSmallest_ext1, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))
result = cfp.getTimeMemoryStr(Solution.kthSmallest_ext2, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))
result = cfp.getTimeMemoryStr(Solution.kthSmallest_ext3, aSolution, aroot, 51000)
print(result['msg'], '执行结果 = {}'.format(result['result']))# 算法本地速度实测比较
函数 kthSmallest_base 的运行时间为 11.97 ms；内存使用量为 756.00 KB 执行结果 = 50999
函数 kthSmallest_ext1 的运行时间为 9.97 ms；内存使用量为 0.00 KB 执行结果 = 50999
函数 kthSmallest_ext2 的运行时间为 8.98 ms；内存使用量为 0.00 KB 执行结果 = 50999
函数 kthSmallest_ext3 的运行时间为 8.98 ms；内存使用量为 8.00 KB 执行结果 = 50999

5. 进阶算法

**进阶：**如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法

思路：

1. 保存一个二叉搜索树的遍历列表和一个修改计数器【默认值为0】
2. 发生插入/删除操作时更新计数器【+1】
3. 查询第k小的值时检测计数器，如果计数器大于0则更新遍历列表，如果计数器等于0则直接取值
4. 代码示意如下

class Solution:def __init__(self, root):self.imodify = 0self.list_inorder = [root]def insertnode(self, treenode):self.imodify += 1# do insert nodedef deletenode(self, treenode):self.imodify += 1# do delete nodedef refresh_inorderlist(self, root):self.list_inorder.clear()stack, tmpnode = [], rootwhile tmpnode or stack:if tmpnode:stack.append(tmpnode)tmpnode = tmpnode.leftelse:curnode = stack.pop()self.list_inorder.append(curnode.val)tmpnode = curnode.right      def kthSmallest(self, root, k):if self.imodify > 0:self.refresh_inorderlist(root)self.imodify = 0return self.list_inorder[k-1]

一日练，一日功，一日不练十日空

may the odds be ever in your favor ~