单调栈题目总结-编程知识

单调栈

496. 下一个更大元素 I

503. 下一个更大元素 II

739. 每日温度

6227. 下一个更大元素 IV

模版归纳

「单调栈」顾名思义就是具有单调性的栈结构，一般常用于找到下一个更大的元素，即当前元素右侧第一个更大的元素

看下面一个例子：2 1 2 4 3
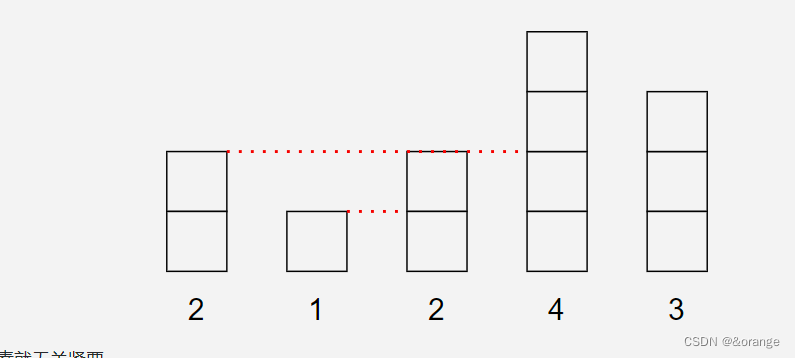
在这里插入图片描述

我们只看得到比我们更高的元素，所以比我们矮的元素就无关紧要

下面给出「单调栈」的模版：

int[] nextGreaterElement(int[] nums) {int n = nums.length;// 存放答案的数组int[] res = new int[n];Stack<Integer> s = new Stack<>(); // 倒着往栈里放for (int i = n - 1; i >= 0; i--) {// 判定个子高矮while (!s.isEmpty() && s.peek() <= nums[i]) {// 矮个起开，反正也被挡着了s.pop();}// nums[i] 身后的更大元素res[i] = s.isEmpty() ? -1 : s.peek();s.push(nums[i]);}return res;
}

现在给几个变形

如果我们现在需要找到下一个大于等于的元素，怎么办？很简单只需要修改一个地方即可：

// 注意：我们把 s.peek() == nums[i] 的元素留下了
while (!s.isEmpty() && s.peek() < nums[i]) {// 矮个起开，反正也被挡着了s.pop();
}

如果我们现在需要找到下一个更小的元素，怎么办？很简单只需要修改一个地方即可：

while (!s.isEmpty() && s.peek() >= nums[i]) {// 高个起开，太碍眼了s.pop();
}

如果我们现在需要找到上一个更大的元素，怎么办？很简单只需要变换一下遍历顺序即可：

// 正着往栈里放
for (int i = 0; i < n; i++) {// 其他逻辑不变
}

题目实战

上面给出了「单调栈」的模版以及几种不同的变形，下面来几道题目练练手！！

下一个更大元素 I

题目详情可见下一个更大元素 I

这个题目基本上就是一个模版题，处理上用到了一个小技巧

由于nums1是nums2的子集，所以我们先求出nums2的所有下一个更大元素，用Map映射保存一下即可

public int[] nextGreaterElement(int[] nums1, int[] nums2) {Map<Integer, Integer> greaterMap = new HashMap<>();Stack<Integer> stack = new Stack<>();for (int i = nums2.length - 1; i >= 0; i--) {while (!stack.isEmpty() && stack.peek() <= nums2[i]) stack.pop();// 保存 nums2[i] 下一个更大元素greaterMap.put(nums2[i], stack.isEmpty() ? -1 : stack.peek());stack.push(nums2[i]);}int[] res = new int[nums1.length];// 寻找 nums1 中元素在 nums2 中的下一个更大元素for (int i = 0; i < nums1.length; i++) {res[i] = greaterMap.get(nums1[i]);}return res;
}

下一个更大元素 II

题目详情可见下一个更大元素 II

这个问题加入了一个循环数组的概念，我们处理的方法就是利用 2 倍的数组即可

为了节约空间，我们可以利用「模运算」实现 2 倍数组的效果，而不需要单独开辟空间

public int[] nextGreaterElements(int[] nums) {int n = nums.length;int[] res = new int[n];Stack<Integer> stack = new Stack<>();for (int i = 2 * n - 1; i >= 0; i--) {while (!stack.isEmpty() && stack.peek() <= nums[i % n]) stack.pop();res[i % n] = stack.isEmpty() ? -1 : stack.peek();stack.push(nums[i % n]);}return res;
}

每日温度

题目详情可见每日温度

这个问题需要让我们求与下一个更大元素的间隔，所以我们稍微转变一下栈中存储的内容即可

模版中存储的内容为num[i]，这样就损失了下一个更大元素的位置信息。如果我们改为存储「下标」，既保留了位置信息，也可以通过下标获得值

public int[] dailyTemperatures(int[] temperatures) {int[] res = new int[temperatures.length];Stack<Integer> stack = new Stack<>();for (int i = temperatures.length - 1; i >= 0; i--) {while (!stack.isEmpty() && temperatures[stack.peek()] <= temperatures[i]) stack.pop();res[i] = stack.isEmpty() ? 0 : stack.peek() - i;stack.push(i);}return res;
}

下一个更大元素 IV

题目详情可见下一个更大元素 IV

这个题目更形象的名字应该是：下下个更大的元素

public int[] secondGreaterElement(int[] nums) {int n = nums.length;int[] ans = new int[n];Arrays.fill(ans, -1);// s1 用来存储还没有遇到「比它大的下一个元素」的元素Deque<Integer> s1 = new ArrayDeque<>();// s2 用来存储遇到一个「比它大的下一个元素」的元素Deque<Integer> s2 = new ArrayDeque<>();for (int i = 0; i < nums.length; i++) {// 如果 s2 中有比 nums[i] 小的元素，说明 nums[i] 就是该元素的下下个更大的元素while (!s2.isEmpty() && nums[i] > nums[s2.peek()]) ans[s2.poll()] = nums[i];Deque<Integer> t = new ArrayDeque<>();// 如果 s1 中有比 nums[i] 小的元素，说明该元素遇到了一个「比它大的下一个元素」的元素，移到 s2 中// 注意：需要按顺序移动！！比如在 s1 中的顺序是 a1 a2 a3，那么移到 s2 中的存储顺序也应该 a1 a2 a3// 所以这里借助另外一个栈来中转一下，不然顺序会反转while (!s1.isEmpty() && nums[i] > nums[s1.peek()]) t.push(s1.poll());s1.push(i);while (!t.isEmpty()) s2.push(t.poll());}return ans;
}

其实除了用两个栈，还可以用两个堆来实现，堆比栈更好理解，但是原理都是一样的！

public int[] secondGreaterElement(int[] nums) {int n = nums.length;int[] ans = new int[n];Arrays.fill(ans, -1);// 小根堆Queue<Integer> q1 = new PriorityQueue<>((a, b) -> nums[a] - nums[b]);Queue<Integer> q2 = new PriorityQueue<>((a, b) -> nums[a] - nums[b]);for (int i = 0; i < n; i++) {int x = nums[i];while (!q2.isEmpty() && nums[q2.peek()] < x) ans[q2.poll()] = x;while (!q1.isEmpty() && nums[q1.peek()] < x) q2.offer(q1.poll());q1.offer(i); }return ans;
}

引用