目录
神经网络整体框架
核心计算步骤
参数初始化
矩阵拉伸与还原
前向传播
损失函数定义
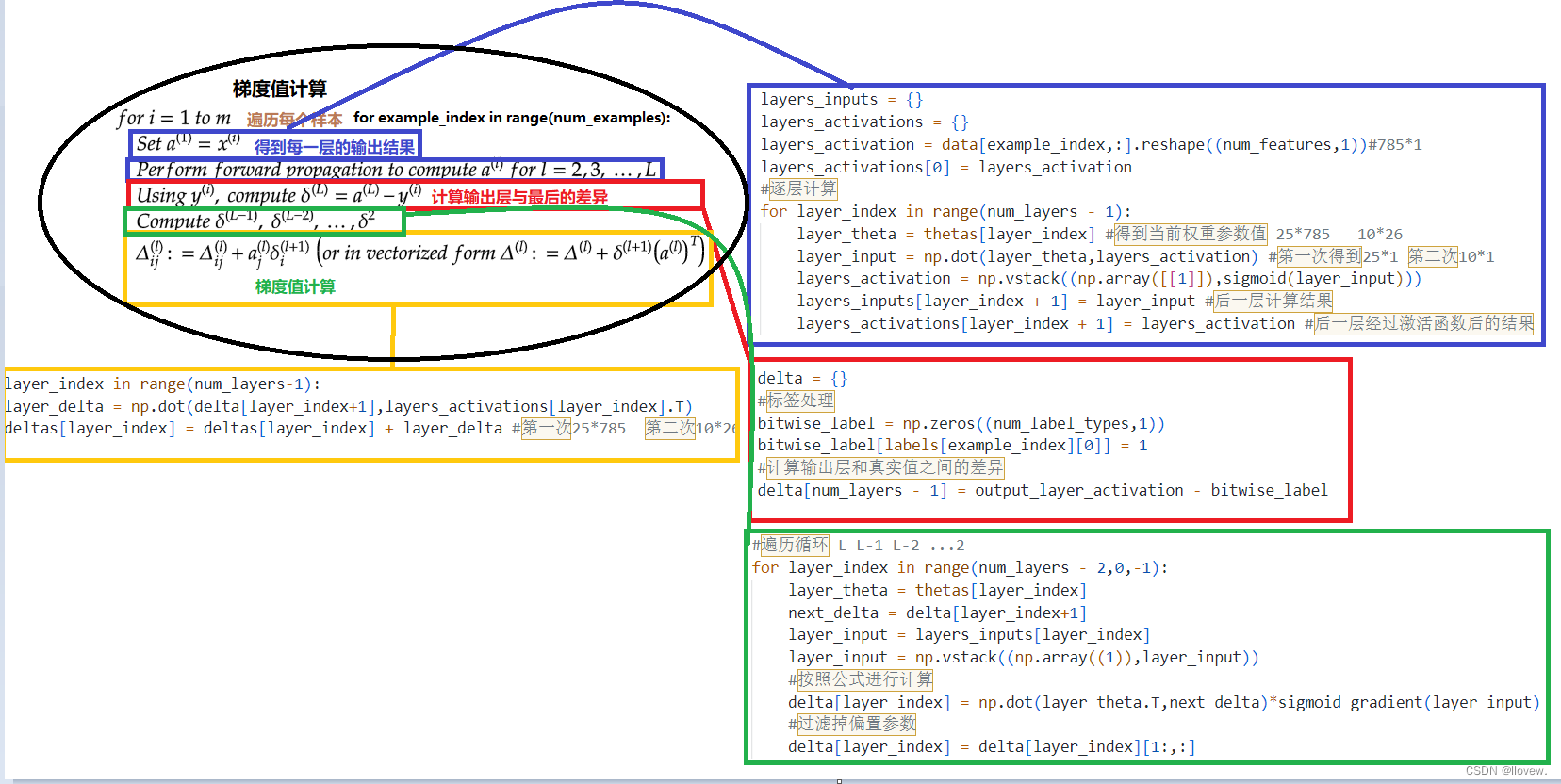
反向传播
全部迭代更新完成
数字识别实战
神经网络整体框架

核心计算步骤
参数初始化
# 定义初始化函数 normalize_data是否需要标准化def __init__(self,data,labels,layers,normalize_data=False):# 数据处理data_procesed = prepare_for_training(data,normalize_data = normalize_data)# 获取当前处理好的数据self.data = data_procesedself.labels = labels# 定义神经网络层数self.layers = layers #784(28*28*1)| 像素点 25(隐层神经元)| 10(十分类任务)self.normalize_data = normalize_data# 初始化权重参数self.thetas = MultilayerPerceptron.thetas_init(layers)@staticmethoddef thetas_init(layers):# 层的个数num_layers = len(layers)# 构建多组权重参数thetas = {}# 会执行两次,得到两组参数矩阵:25*785 , 10*26for layer_index in range(num_layers - 1):# 输入in_count = layers[layer_index] #784# 输出out_count = layers[layer_index+1]# 构建矩阵并初始化操作 随机进行初始化操作,值尽量小一点thetas[layer_index] = np.random.rand(out_count,in_count+1)*0.05 # WX in_count+1:偏置项考虑进去,偏置项个数跟输出的结果一致return thetas矩阵拉伸与还原
# 将25*785矩阵拉长1*19625@staticmethoddef thetas_unroll(thetas):num_theta_layers = len(thetas) #25*785 , 10*26;num_theta_layers长度为2unrolled_theta = np.array([])for theta_layer_index in range(num_theta_layers):# thetas[theta_layer_index].flatten()矩阵拉长# np.hstack((unrolled_theta, thetas[theta_layer_index].flatten())) 数组拼接 将25*785 , 10*26两个矩阵拼接成一个 1*x的矩阵unrolled_theta = np.hstack((unrolled_theta, thetas[theta_layer_index].flatten()))return unrolled_theta# 矩阵还原"""将展开的`unrolled_thetas`重新组织成一个字典`thetas`,其中每个键值对表示一个层的权重阵。函数的输入参数包括展开的参数`unrolled_thetas`和神经网络的层结构`layers`。具体来说,函数首先获取层的数量`num_layers`,然后创建一个空字典`thetas`用于存储权重矩阵。接下来,函数通过循环遍历每一层(除了最后一层),并根据层的输入和输出节点数计算权重矩阵的大小。在循环中,函数首先计算当前层权重矩阵的宽度`thetas_width`和高度`thetas_height`,然后计算权重矩阵的总元素个数`thetas_volume`。接着,函数根据展开参数的索引范围提取对应层的展开权重,并通过`reshape`函数将展开权重重新组织成一个二维矩阵。最后,函数将该矩阵存储到字典`thetas`中,键为当前层的索引。循环结束后,函数返回字典`thetas`,其中包含了每一层的权重矩阵。"""@staticmethoddef thetas_roll(unrolled_thetas,layers):# 进行反变换,将行转换为矩阵num_layers = len(layers)# 包含第一层、第二层、第三层thetas = {}# 指定标识符当前变换到哪了unrolled_shift = 0# 构造想要的参数矩阵for layer_index in range(num_layers - 1):# 输入in_count = layers[layer_index]# 输出out_count = layers[layer_index + 1]# 构造矩阵thetas_width = in_count + 1thetas_height = out_count# 计算权重矩阵的总元素个数thetas_volume = thetas_width * thetas_height# 指定从矩阵中哪个位置取值start_index = unrolled_shift# 结束位置end_index = unrolled_shift + thetas_volumelayer_theta_unrolled = unrolled_thetas[start_index:end_index]# 获得25*785和10*26两个矩阵thetas[layer_index] = layer_theta_unrolled.reshape((thetas_height, thetas_width))# 更新unrolled_shift = unrolled_shift + thetas_volumereturn thetas前向传播
# 前向传播函数@staticmethoddef feedforward_propagation(data,thetas,layers):# 获取层数num_layers = len(layers)# 样本个数num_examples = data.shape[0]# 定义输入层in_layer_activation = data# 逐层计算for layer_index in range(num_layers - 1):theta = thetas[layer_index]# 隐藏层得到的结果out_layer_activation = sigmoid(np.dot(in_layer_activation, theta.T))# 正常计算完之后是num_examples*25,但是要考虑偏置项 变成num_examples*26out_layer_activation = np.hstack((np.ones((num_examples, 1)), out_layer_activation))in_layer_activation = out_layer_activation# 返回输出层结果,结果中不要偏置项了return in_layer_activation[:, 1:]损失函数定义
# 损失函数定义@staticmethoddef cost_function(data,labels,thetas,layers):# 获取层数num_layers = len(layers)# 样本个数num_examples = data.shape[0]# 分类个数num_labels = layers[-1]# 前向传播走一次predictions = MultilayerPerceptron.feedforward_propagation(data, thetas, layers)# 制作标签,每一个样本的标签都得是one-hotbitwise_labels = np.zeros((num_examples, num_labels))for example_index in range(num_examples):# 将对应的位置改为 1bitwise_labels[example_index][labels[example_index][0]] = 1# 计算损失bit_set_cost = np.sum(np.log(predictions[bitwise_labels == 1]))bit_not_set_cost = np.sum(np.log(1 - predictions[bitwise_labels == 0]))cost = (-1 / num_examples) * (bit_set_cost + bit_not_set_cost)return cost反向传播
# 反向传播函数@staticmethoddef back_propagation(data, labels, thetas, layers):# 获取层数num_layers = len(layers)# 样本个数、特征个数(num_examples, num_features) = data.shape# 输出结果num_label_types = layers[-1]# 输出层跟结果之间的差异deltas = {}# 初始化操作 逐层定义当前的值for layer_index in range(num_layers - 1):in_count = layers[layer_index]out_count = layers[layer_index + 1]# 构建矩阵deltas[layer_index] = np.zeros((out_count, in_count + 1)) # 得到两个矩阵25*785 10*26# 遍历输入层每个样本for example_index in range(num_examples):# 得到每层的输出结果layers_inputs = {}layers_activations = {}# 第0层输入转换为向量个数 输入层结果layers_activation = data[example_index, :].reshape((num_features, 1)) # 785*1layers_activations[0] = layers_activation# 逐层计算for layer_index in range(num_layers - 1):layer_theta = thetas[layer_index] # 得到当前权重参数值 25*785 10*26layer_input = np.dot(layer_theta, layers_activation) # 第一次得到25*1 第二次10*1 第一层输出等于第二层输入layers_activation = np.vstack((np.array([[1]]), sigmoid(layer_input)))layers_inputs[layer_index + 1] = layer_input # 后一层计算结果layers_activations[layer_index + 1] = layers_activation # 后一层经过激活函数后的结果output_layer_activation = layers_activation[1:, :] #去除偏置参数delta = {}# 标签处理bitwise_label = np.zeros((num_label_types, 1))bitwise_label[labels[example_index][0]] = 1# 计算输出层和真实值之间的差异delta[num_layers - 1] = output_layer_activation - bitwise_label# 遍历循环 L L-1 L-2 ...2for layer_index in range(num_layers - 2, 0, -1):layer_theta = thetas[layer_index]next_delta = delta[layer_index + 1]layer_input = layers_inputs[layer_index]layer_input = np.vstack((np.array((1)), layer_input))# 按照公式进行计算delta[layer_index] = np.dot(layer_theta.T, next_delta) * sigmoid_gradient(layer_input)# 过滤掉偏置参数delta[layer_index] = delta[layer_index][1:, :]# 梯度值计算for layer_index in range(num_layers - 1):layer_delta = np.dot(delta[layer_index + 1], layers_activations[layer_index].T)deltas[layer_index] = deltas[layer_index] + layer_delta # 第一次25*785 第二次10*26for layer_index in range(num_layers - 1):deltas[layer_index] = deltas[layer_index] * (1 / num_examples)return deltas
全部迭代更新完成
import numpy as np
from utils.features import prepare_for_training
from utils.hypothesis import sigmoid,sigmoid_gradientclass MultilayerPerceptron:# 定义初始化函数 normalize_data是否需要标准化def __init__(self,data,labels,layers,normalize_data=False):# 数据处理data_procesed = prepare_for_training(data,normalize_data = normalize_data)# 获取当前处理好的数据self.data = data_procesedself.labels = labels# 定义神经网络层数self.layers = layers #784(28*28*1)| 像素点 25(隐层神经元)| 10(十分类任务)self.normalize_data = normalize_data# 初始化权重参数self.thetas = MultilayerPerceptron.thetas_init(layers)@staticmethoddef thetas_init(layers):# 层的个数num_layers = len(layers)# 构建多组权重参数thetas = {}# 会执行两次,得到两组参数矩阵:25*785 , 10*26for layer_index in range(num_layers - 1):# 输入in_count = layers[layer_index] #784# 输出out_count = layers[layer_index+1]# 构建矩阵并初始化操作 随机进行初始化操作,值尽量小一点thetas[layer_index] = np.random.rand(out_count,in_count+1)*0.05 # WX in_count+1:偏置项考虑进去,偏置项个数跟输出的结果一致return thetas# 将25*785矩阵拉长1*19625@staticmethoddef thetas_unroll(thetas):num_theta_layers = len(thetas) #25*785 , 10*26;num_theta_layers长度为2unrolled_theta = np.array([])for theta_layer_index in range(num_theta_layers):# thetas[theta_layer_index].flatten()矩阵拉长# np.hstack((unrolled_theta, thetas[theta_layer_index].flatten())) 数组拼接 将25*785 , 10*26两个矩阵拼接成一个 1*x的矩阵unrolled_theta = np.hstack((unrolled_theta, thetas[theta_layer_index].flatten()))return unrolled_theta# 矩阵还原"""将展开的`unrolled_thetas`重新组织成一个字典`thetas`,其中每个键值对表示一个层的权重阵。函数的输入参数包括展开的参数`unrolled_thetas`和神经网络的层结构`layers`。具体来说,函数首先获取层的数量`num_layers`,然后创建一个空字典`thetas`用于存储权重矩阵。接下来,函数通过循环遍历每一层(除了最后一层),并根据层的输入和输出节点数计算权重矩阵的大小。在循环中,函数首先计算当前层权重矩阵的宽度`thetas_width`和高度`thetas_height`,然后计算权重矩阵的总元素个数`thetas_volume`。接着,函数根据展开参数的索引范围提取对应层的展开权重,并通过`reshape`函数将展开权重重新组织成一个二维矩阵。最后,函数将该矩阵存储到字典`thetas`中,键为当前层的索引。循环结束后,函数返回字典`thetas`,其中包含了每一层的权重矩阵。"""@staticmethoddef thetas_roll(unrolled_thetas,layers):# 进行反变换,将行转换为矩阵num_layers = len(layers)# 包含第一层、第二层、第三层thetas = {}# 指定标识符当前变换到哪了unrolled_shift = 0# 构造想要的参数矩阵for layer_index in range(num_layers - 1):# 输入in_count = layers[layer_index]# 输出out_count = layers[layer_index + 1]# 构造矩阵thetas_width = in_count + 1thetas_height = out_count# 计算权重矩阵的总元素个数thetas_volume = thetas_width * thetas_height# 指定从矩阵中哪个位置取值start_index = unrolled_shift# 结束位置end_index = unrolled_shift + thetas_volumelayer_theta_unrolled = unrolled_thetas[start_index:end_index]# 获得25*785和10*26两个矩阵thetas[layer_index] = layer_theta_unrolled.reshape((thetas_height, thetas_width))# 更新unrolled_shift = unrolled_shift + thetas_volumereturn thetas# 损失函数定义@staticmethoddef cost_function(data,labels,thetas,layers):# 获取层数num_layers = len(layers)# 样本个数num_examples = data.shape[0]# 分类个数num_labels = layers[-1]# 前向传播走一次predictions = MultilayerPerceptron.feedforward_propagation(data, thetas, layers)# 制作标签,每一个样本的标签都得是one-hotbitwise_labels = np.zeros((num_examples, num_labels))for example_index in range(num_examples):# 将对应的位置改为 1bitwise_labels[example_index][labels[example_index][0]] = 1# 计算损失bit_set_cost = np.sum(np.log(predictions[bitwise_labels == 1]))bit_not_set_cost = np.sum(np.log(1 - predictions[bitwise_labels == 0]))cost = (-1 / num_examples) * (bit_set_cost + bit_not_set_cost)return cost# 梯度值计算函数@staticmethoddef gradient_step(data, labels, optimized_theta, layers):# 将theta值还原成矩阵格式theta = MultilayerPerceptron.thetas_roll(optimized_theta, layers)# 反向传播thetas_rolled_gradients = MultilayerPerceptron.back_propagation(data, labels, theta, layers)# 将矩阵拉伸方便参数更新thetas_unrolled_gradients = MultilayerPerceptron.thetas_unroll(thetas_rolled_gradients)# 返回梯度值return thetas_unrolled_gradients# 梯度下降模块@staticmethoddef gradient_descent(data,labels,unrolled_theta,layers,max_iterations,alpha):# 最终得到的theta值先使用初始thetaoptimized_theta = unrolled_theta# 每次迭代都会得到当前的损失值,记录到 cost_history数组中cost_history = []# 进行迭代for _ in range(max_iterations):# 1.计算当前损失值 thetas_roll()函数将拉长后的向量还原成矩阵cost = MultilayerPerceptron.cost_function(data, labels,MultilayerPerceptron.thetas_roll(optimized_theta, layers), layers)# 记录当前损失cost_history.append(cost)# 2.根据损失值计算当前梯度值theta_gradient = MultilayerPerceptron.gradient_step(data, labels, optimized_theta, layers)# 3.更新梯度值,最终得到的结果是优化完的thetaoptimized_theta = optimized_theta - alpha * theta_gradientreturn optimized_theta, cost_history# 前向传播函数@staticmethoddef feedforward_propagation(data,thetas,layers):# 获取层数num_layers = len(layers)# 样本个数num_examples = data.shape[0]# 定义输入层in_layer_activation = data# 逐层计算for layer_index in range(num_layers - 1):theta = thetas[layer_index]# 隐藏层得到的结果out_layer_activation = sigmoid(np.dot(in_layer_activation, theta.T))# 正常计算完之后是num_examples*25,但是要考虑偏置项 变成num_examples*26out_layer_activation = np.hstack((np.ones((num_examples, 1)), out_layer_activation))in_layer_activation = out_layer_activation# 返回输出层结果,结果中不要偏置项了return in_layer_activation[:, 1:]# 反向传播函数@staticmethoddef back_propagation(data, labels, thetas, layers):# 获取层数num_layers = len(layers)# 样本个数、特征个数(num_examples, num_features) = data.shape# 输出结果num_label_types = layers[-1]# 输出层跟结果之间的差异deltas = {}# 初始化操作 逐层定义当前的值for layer_index in range(num_layers - 1):in_count = layers[layer_index]out_count = layers[layer_index + 1]# 构建矩阵deltas[layer_index] = np.zeros((out_count, in_count + 1)) # 得到两个矩阵25*785 10*26# 遍历输入层每个样本for example_index in range(num_examples):# 得到每层的输出结果layers_inputs = {}layers_activations = {}# 第0层输入转换为向量个数 输入层结果layers_activation = data[example_index, :].reshape((num_features, 1)) # 785*1layers_activations[0] = layers_activation# 逐层计算for layer_index in range(num_layers - 1):layer_theta = thetas[layer_index] # 得到当前权重参数值 25*785 10*26layer_input = np.dot(layer_theta, layers_activation) # 第一次得到25*1 第二次10*1 第一层输出等于第二层输入layers_activation = np.vstack((np.array([[1]]), sigmoid(layer_input)))layers_inputs[layer_index + 1] = layer_input # 后一层计算结果layers_activations[layer_index + 1] = layers_activation # 后一层经过激活函数后的结果output_layer_activation = layers_activation[1:, :] #去除偏置参数delta = {}# 标签处理bitwise_label = np.zeros((num_label_types, 1))bitwise_label[labels[example_index][0]] = 1# 计算输出层和真实值之间的差异delta[num_layers - 1] = output_layer_activation - bitwise_label# 遍历循环 L L-1 L-2 ...2for layer_index in range(num_layers - 2, 0, -1):layer_theta = thetas[layer_index]next_delta = delta[layer_index + 1]layer_input = layers_inputs[layer_index]layer_input = np.vstack((np.array((1)), layer_input))# 按照公式进行计算delta[layer_index] = np.dot(layer_theta.T, next_delta) * sigmoid_gradient(layer_input)# 过滤掉偏置参数delta[layer_index] = delta[layer_index][1:, :]# 梯度值计算for layer_index in range(num_layers - 1):layer_delta = np.dot(delta[layer_index + 1], layers_activations[layer_index].T)deltas[layer_index] = deltas[layer_index] + layer_delta # 第一次25*785 第二次10*26for layer_index in range(num_layers - 1):deltas[layer_index] = deltas[layer_index] * (1 / num_examples)return deltas# 定义训练模块 定义最大迭代次数 定义学习率def train(self,max_iterations=1000,alpha=0.1):"""第一步首先需要做优化,计算损失函数然后根据损失函数计算梯度值,然后更新梯度值调整权重参数,前向传播加反向传播,整体一次迭代"""# 将矩阵转化为向量方便参数更新,将25*785矩阵拉长1*19625unrolled_theta = MultilayerPerceptron.thetas_unroll(self.thetas)# 梯度下降模块(optimized_theta, cost_history) = MultilayerPerceptron.gradient_descent(self.data, self.labels, unrolled_theta,self.layers, max_iterations, alpha)# 参数更新完成之后需要将拉长后的还原,进行前向传播self.thetas = MultilayerPerceptron.thetas_roll(optimized_theta, self.layers)return self.thetas, cost_history数字识别实战
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as mping
import mathfrom multilayer_perceptron import MultilayerPerceptrondata = pd.read_csv('../data/mnist-demo.csv')
numbers_to_display = 25
num_cells = math.ceil(math.sqrt(numbers_to_display))
plt.figure(figsize=(10,10))
for plot_index in range(numbers_to_display):digit = data[plot_index:plot_index+1].valuesdigit_label = digit[0][0]digit_pixels = digit[0][1:]image_size = int(math.sqrt(digit_pixels.shape[0]))frame = digit_pixels.reshape((image_size,image_size))plt.subplot(num_cells,num_cells,plot_index+1)plt.imshow(frame,cmap='Greys')plt.title(digit_label)
plt.subplots_adjust(wspace=0.5,hspace=0.5)
plt.show()train_data = data.sample(frac = 0.8)
test_data = data.drop(train_data.index)train_data = train_data.values
test_data = test_data.valuesnum_training_examples = 1700x_train = train_data[:num_training_examples,1:]
y_train = train_data[:num_training_examples,[0]]x_test = test_data[:,1:]
y_test = test_data[:,[0]]layers=[784,25,10]normalize_data = True
max_iterations = 300
alpha = 0.1multilayer_perceptron = MultilayerPerceptron(x_train,y_train,layers,normalize_data)
(thetas,costs) = multilayer_perceptron.train(max_iterations,alpha)
plt.plot(range(len(costs)),costs)
plt.xlabel('Grident steps')
plt.xlabel('costs')
plt.show()y_train_predictions = multilayer_perceptron.predict(x_train)
y_test_predictions = multilayer_perceptron.predict(x_test)train_p = np.sum(y_train_predictions == y_train)/y_train.shape[0] * 100
test_p = np.sum(y_test_predictions == y_test)/y_test.shape[0] * 100
print ('训练集准确率:',train_p)
print ('测试集准确率:',test_p)numbers_to_display = 64num_cells = math.ceil(math.sqrt(numbers_to_display))plt.figure(figsize=(15, 15))for plot_index in range(numbers_to_display):digit_label = y_test[plot_index, 0]digit_pixels = x_test[plot_index, :]predicted_label = y_test_predictions[plot_index][0]image_size = int(math.sqrt(digit_pixels.shape[0]))frame = digit_pixels.reshape((image_size, image_size))color_map = 'Greens' if predicted_label == digit_label else 'Reds'plt.subplot(num_cells, num_cells, plot_index + 1)plt.imshow(frame, cmap=color_map)plt.title(predicted_label)plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)plt.subplots_adjust(hspace=0.5, wspace=0.5)
plt.show()